Статистика Гусаров 2008. Контрольные вопросы по изучаемому материалу. Для студентов и преподавателей экономических специальностей, а также для специалистов статистических, финансовобанковских, экономических органов, страховых компаний и коммерческих структур
 Скачать 9.51 Mb.
|
27.1.5. Определение наращенной суммы по смешанным процентным ставкамНаращение по смешанным процентным ставкам применяется для случаев, когда и не является целым числом:  где nа– целое число лет; nb – дробная часть года. Сопоставление формул наращения по простым и сложным процентам позволяет сделать вывод: если n < 1, то (1 + ni) > (1 + i)n – сложные проценты меньше простых; если n = 1, то (1 + ni) = (1 + i)n – сложные проценты равны простым; если n > 1, то (1 + ni) < (1 + i)n – сложные проценты больше простых, где n – число периодов начисления процентов. 27.1.6. Эквивалентные ставкиЗаписав равенство, найдем ставку простых процентов, эквивалентную ставке сложных процентов: 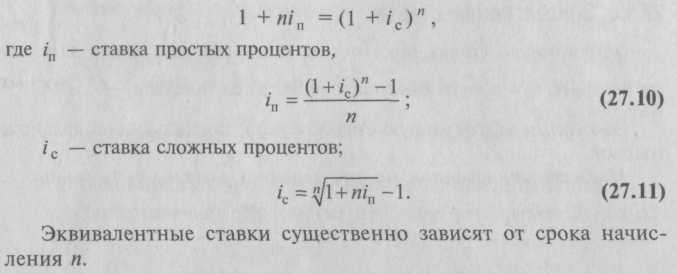 27.1.7. Номинальная ставкаВ современных условиях проценты капитализируются обычно не один, а несколько, т раз в году: по полугодиям, кварталам и т.д. Некоторые зарубежные коммерческие банки практикуют ежедневное начисление процентов. В таком случае годовая ставка называется номинальной ставкой процентов и обозначается через j. Тогда при т раз начислений процентов в году ставка, действительно начисляемая в каждом периоде, будет равна  Формула наращения сложных процентов (при т раз начислений в году):  Увеличение т приводит к более быстрому процессу наращения, так как чаще происходит капитализация процентов. При большом числе периодов наращенная сумма может достичь астрономической величины, поэтому нельзя допускать возможность помещать капитал на очень большой срок. Задача 5. Изменим одно условие в задаче 4. Пусть теперь проценты начисляются поквартально. Требуется найти наращенную сумму. В этом случае: n = 5 лет; т = 4 квартала. Решение. Наращенная сумма составит:  27.1.8. Эффективная ставкаЭффективная ставка показывает, какая годовая ставка дает тот же процент, что и m-разовое наращение в год по ставке  Обозначим эффективную ставку через i, поскольку она является годовой.Множители наращения, по определению, должны быть равны:  Следовательно, эффективная ставка:  Как видим, эффективная ставка при т > 1 больше номинальной, при т = 1 равна ей: i = j. Замена в договоре номинальной ставки jпри m-разовом начислении процентов на эффективную ставку i не изменяет финансовых обязательств участвующих сторон, так как обе ставки эквивалентны в финансовом отношении. Задача 6. Определите эффективную ставку, если номинальная ставка равна 25% при помесячном начислении. 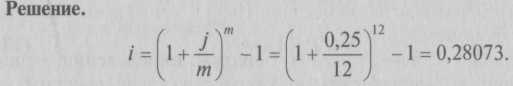 Для сторон безразлично: применять ли ставку 25% (при помесячном начислении) или годовую ставку 28,073%. При подготовке контрактов может возникнуть необходимость и в решении обратной задачи – определение jпо заданным значениям iи т. Находим номинальную ставку.  Задача 7. В какой банк выгоднее поместить деньги сроком на 2 года в сумме 3 тыс. руб. на депозитный вклад: в первый банк под 6% годовых с ежеквартальной капитализацией или во второй банк под 4% годовых с ежемесячной капитализацией?  |