Курс лекции по геодезии. Курс лекции по геодезии Акрам, руси. Лекция по дисциплине Геодезия Лекция Определение геодезии как науки и ее задачи. История геодезии
 Скачать 2.09 Mb. Скачать 2.09 Mb.
|
|
Косвенные измерения – такие измерения, которые получают по формулам, связывающим значения измеренных физических величин со значениями других физических величин, полученных из прямых измерений и являющихся аргументами этих формул. Уравнение косвенного измерения λ= f (λ1,λ2,λ3,...,λn). Ошибки измерений Процесс измерений протекает во времени и определенных условиях, в нём участвуют объект измерения, измерительный прибор, наблюдатель и среда, в которой выполняют измерения. В связи с этим на результаты измерений влияют качество измерительных приборов, квалификация наблюдателя, состояние измеряемого объекта и изменения среды во времени. При многократном измерении одной и той же величины из-за влияния перечисленных факторов результаты измерений могут отличаться друг от друга и не совпадать со значением измеряемой величины. Разность между результатом измерения и действительным значением измеряемой величины называется ошибкой результата измерения. По характеру и свойствам ошибки подразделяют на: грубые; систематические; случайные. Грубые ошибки или просчеты легко обнаружить при повторных измерениях или при внимательном отношении к измерениям. Систематические ошибки – те, которые действуют по определенным законам и сохраняют один и тот же знак. Систематические ошибки можно учесть в результатах измерений, если найти функциональную зависимость и с её помощью исключить ошибку или уменьшить её до малой величины. Случайные ошибки – результат действия нескольких причин. Величина случайной ошибки зависит от того, кто измеряет, каким методом и в каких условиях. Случайными эти ошибки называются потому, что каждый из факторов действует случайно. Их нельзя устранить, но уменьшить влияние можно увеличением числа измерений. Свойства случайных ошибок измерений Теория ошибок изучает только случайные ошибки. Под случайной ошибкой здесь и далее будем понимать разность Δi = Х – ℓi гдеΔi– истинная случайная ошибка; Х – истинная величина; ℓi – измеренная величина. Случайные ошибки имеют следующие свойства: 1. Чем меньше по абсолютной величине случайная ошибка, тем она чаще встречается при измерениях. Одинаковые по абсолютной величине случайные ошибки одинаково часто встречаются при измерениях. При данных условиях измерений величина случайной погрешности по абсолютной величине не превосходит некоторого предела. Под данными условиями подразумевается один и тот же прибор, один и тот же наблюдатель, одни и те же параметры внешней среды. Такие измерения называют равноточными. 4. Среднее арифметическое из случайных ошибок стремиться к нулю при неограниченном возрастании числа измерений. Три первых свойства случайных ошибок достаточно очевидны. Четвертое свойство вытекает из второго. Если Δ1,Δ2,Δ3,...,Δn - случайные ошибки отдельных измерений, где n – число измерений, то четвертое свойство случайных ошибок математически выражается 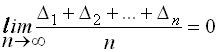 Предел этого отношения будет равен нулю, потому что в числителе сумма случайных ошибок будет конечной величиной, так как положительные и отрицательные случайные ошибки при сложении будут компенсироваться. Чтобы запись была компактной, Гаусс предложил сумму записывать символом тогда 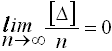 Оценка точности результатов измерений Под точностью измерений понимается степень близости результата измерения к истинному значению измеряемой величины. Точность результата измерений зависит от условий измерений. Для равноточных результатов измерений мерой точности является средняя квадратическая ошибка m, определяемая по формуле Гаусса: 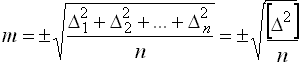 . .Средняя квадратическая ошибка обладает устойчивостью при небольшом числе измерений. Предельная ошибка. Вследствие третьего свойства случайные ошибки, превышающие по абсолютной величине значение 2m, встречаются редко (5 на 100 измерений). Еще реже погрешности больше 3m (3 из 1000 измерений). Поэтому устроенную погрешность называют предельной ошибкой Для особо точных измерений в качестве предельной ошибки принимают Все вышеперечисленные ошибки называют абсолютными. В геодезии в качестве специальных характеристик точности измерений используется относительная ошибка – отношение абсолютной ошибки к среднему значению измеряемой величины, которое выражается в виде простой дроби с единицей в числителе, например Средняя квадратическая ошибка функции общего вида В большинстве случаев геодезические измерения выполняют с целью определения значения других величин, связанных с измеряемой функциональной зависимостью. Например: D = К · n ; h = З – П ; h = S · tgν. Для суждения о получаемой при этом точности необходимо определить среднюю квадратическую ошибку функции по средним квадратическим ошибкам исходных величин, которые в свою очередь, могут являться результатами измерений или функциями результатов измерений. Пусть u = f(X,Y,Z) есть некоторая функция независимых величин X, Y, Z, измеренных или вычисленных со средними квадратическими ошибками mx, my, mz. Продифференцируем функцию по всем переменным и получим В этой формуле бесконечно малые приращения – дифференциалы – заменим истинными ошибками. Получим выражение 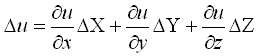 , ,где ΔX, ΔY, ΔZ – истинные ошибки. Перейдем от истинных ошибок к средним квадратическим ошибкам. Для этого положим, что X, Y, Z измерено n раз, где можно считать 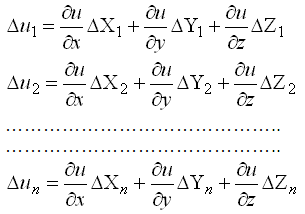 Возведем каждое из равенств в квадрат, сложим и разделим на n 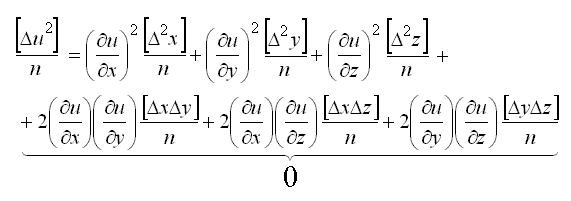 А так как 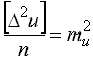 ; ; 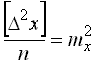 и т.д., и т.д.,то 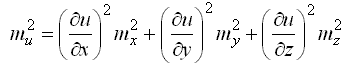 где Лекция 17. Геодезические сети. Государственные геодезические сети, сети сгущения. Съемочные сети. Геодезические знаки. Принцип организации съемочных работ Геодезические измерения сводятся к определению взаимного положения точек на земной поверхности. Чтобы ослабить влияние ошибок измерений и не допустить их накопления при геодезической съемке участков местности, принято за правило вести работу от общего к частному. Для этого из множества определяемых точек участка земной поверхности выделяют наиболее характерные и определяют в первую очередь их положение. Такие точки называют опорными. Эти точки образуют геодезическую опорную сеть (геодезическое основание), т.е. составляют как бы общую канву, на основе которой с необходимой, хотя и более низкой точностью производится дальнейшая съемка. Для того, чтобы результаты съемок были надежны, все важнейшие геодезические действия должны выполняться с контролем. Поэтому в основе качества геодезических работ лежит принцип ни одного шага вперед без контроля предыдущих действий. Назначение и виды государственных геодезических сетей Одной из важнейших задач данного государственного органа является создание государственной геодезической сети (ГГС) на территории нашей страны. Государственной геодезической сетью является совокупность опорных геодезических пунктов, прочно закрепленных на местности, взаимное расположение которых точно определено в единой государственной системе координат и высот. Геодезические сети подразделяются на государственную геодезическую сеть, геодезическую сеть сгущения и съемочную геодезическую сеть. Государственная геодезическая сеть является исходной для других геодезических сетей. Она делится на плановую и высотную. Плановая государственная геодезическая сеть создается астрономическим или геодезическим методами. При астрономическом методе плановое положение каждого из отдельных пунктов сети определяется независимо друг от друга из астрономических наблюдений. Геодезический метод состоит в том, что для определения координат точек находят из астрономических наблюдений координаты только нескольких точек, называемых исходными. Дальнейшее определения планового положения точек производят путем геодезических измерений на местности. Высотная государственная геодезическая сеть создается методом геометрического нивелирования. Плановые государственные геодезические сети. Методы их создания Основными методами создания государственной геодезической сети являются триангуляция, трилатерация, полигонометрия и спутниковые координатные определения. Триангуляция (рис. 68, а) представляет собой цепь прилегающих друг к другу треугольников, в каждом из которых измеряют высокоточными теодолитами все углы. Кроме того, измеряю длины сторон в начале и конце цепи. 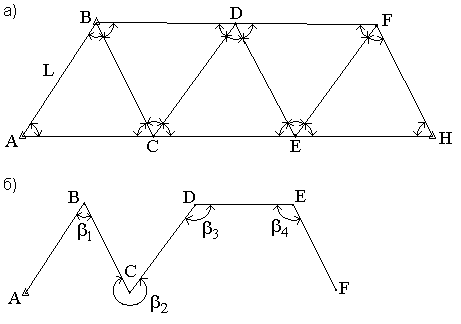 Рис. 68. Схема триангуляции (а) и полигонометрии (б).] В сети триангуляции известными являются базис L и координаты пунктов А и В. Для определения координат остальных пунктов сети измеряют в треугольниках горизонтальные углы. Триангуляция делится на классы 1, 2, 3, 4. Треугольники разных классов различаются длинами сторон и точностью измерения углов и базисов. Развитие сетей триангуляции выполняется с соблюдением основного принципа «от общего к частному», т.е. сначала строится триангуляция 1 класса, а затем последовательно 2, 3 и 4 классов. Пункты государственной геодезической сети закрепляются на местности центрами. Для обеспечения взаимной видимости между пунктами над центрами устанавливают геодезические знаки деревянные или металлические. Они имеют приспособление для установки прибора, платформу для наблюдателя и визирное устройство. В зависимости от конструкции, наземные геодезические знаки подразделяются на пирамиды и простые и сложные сигналы. Типы подземных центров устанавливаются в зависимости от физико-географических условий региона, состава грунта и глубины сезонного промерзания грунта. Например, центр пункта государственной геодезической сети 1-4 классов типа 1 согласно инструкции «Центры и реперы государственной геодезической сети» (М., Недра, 1973) предназначен для южной зоны сезонного промерзания грунтов. Он состоит из железобетонного пилона сечением 16Х16 см (или асбоцементной трубы 14-16 см, заполненной бетоном) и бетонного якоря. Пилон цементируется в якорь. Основание центра должно располагаться ниже глубины сезонного промерзания грунта не менее 0,5 м и не менее 1,3 м от поверхности земли. В верхней части знака на уровне поверхности земли бетонируется чугунная марка. Над маркой в радиусе 0,5 м насыпается грунт слоем 10-15 см. В 1,5м от центра устанавливается опознавательный столб с охранной плитой. В настоящее время широко используют радиотехнические средства для определения расстояний между пунктами сети с относительными ошибками 1:100 000 – 1:1 000 000. Это дает возможность строить геодезические сети методом трилатерации, при которой в сетях треугольников производится только измерение сторон. Величины углов вычисляют тригонометрическим способом. Метод полигонометрии (рис. 68, б) состоит в том, что опорные геодезические пункты связывают между собой ходами, называемыми полигонометрическими. В них измеряют расстояния и справа лежащие углы. Спутниковые методы создания геодезических сетей подразделяются на геометрические и динамические. В геометрическом методе искусственный спутник Земли используют как высокую визирную цель, в динамическом – ИСЗ является носителем координат. Лексия 17. Высотные государственные геодезические сети Государственная высотная геодезическая сеть – это нивелирная сеть I, II, III и IV классов. При этом сети I и II классов являются высотной основой, с помощью которой устанавливается единая система высот на всей территории страны. На линиях I, II, III и IV классов закладывают вековые, фундаментальные, грунтовые, скальные, стенные и временные реперы. Вековые и фундаментальные реперы закладываются в скальные породы или в грунт. Они отличаются повышенной устойчивостью и обеспечивают сохранность высотной основы на длительное время. Вековыми реперами закрепляют места пересечений линий нивелирования I класса, а фундаментальные – закладывают на линиях I и II классов не реже, чем через 60 км. Временные реперы используют в качестве высотной основы при топографических съёмках, а также включают в линии нивелирования II, III и IV классов. Геодезические съемочные сети Съемочные сети являются геодезической основой при решении инженерно-геодезических задач. Их создают в качестве съемочного обоснования для производства топографических съемок, выноса на местность инженерных сооружений, а также для плановой и высотной привязки отдельных объектов. Съемочное обоснование разбивается от пунктов плановых и высотных опорных сетей. Самый распространенный вид съемочного обоснования – теодолитные ходы (рис. 69), опирающиеся на один или два исходных пункта. Они представляют собой геодезические построения в виде ломаных линий, в которых углы измеряют одним полным приёмом с помощью технического теодолита, а стороны – стальной 20-метровой лентой или дальномерами, обеспечивающими заданную точность. Теодолитные ходы могут быть замкнутыми или разомкнутыми. 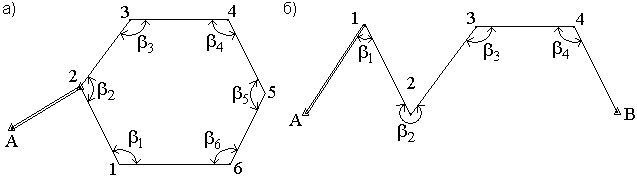 Рис. 69. Теодолитные ходы: замкнутый (а); разомкнутый (б). Длины линий (сторон) теодолитных ходов зависят от масштаба съемки и условий снимаемой местности и должны быть не более 350 м и не менее 20 м. Относительные линейные невязки в ходах должны быть менее 1:2000, при неблагоприятных условиях измерений допускается 1:1000. Углы поворота на точках хода измеряют теодолитом со средней квадратической ошибкой 0,5' одним приемом. Расхождение значений углов в полуприемах не более двойной точности теодолита. Точки съемочного обоснования, как правило, закрепляют на местности временными знаками: деревянными кольями, столбами, металлическими штырями, трубами. Если эти точки предполагается использовать в дальнейшем для других целей, их закрепляют постоянными знаками. Плановая привязка вершин теодолитного хода к пунктам ГГС Совокупность геодезических измерений и вычислений, необходимых для определения положения вершин теодолитного хода в государственной системе координат, называется привязкой Привязку можно выполнить несколькими методами. Плановая привязка методом угловой засечки (рис. 70). 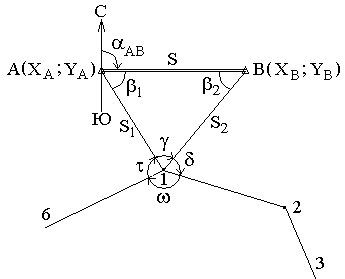 Рис. 70. Привязка теодолитного хода методом угловой засечки. Дано: А Измереные углы: Контроль измерений: Найти координаты точки 1 1. Решение обратной геодезической задачи 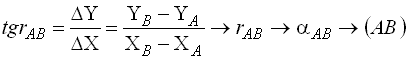 Контроль : 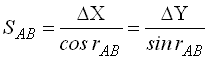 2. Решение треугольника привязки 3. Передача дирекционных углов Контроль вычислений: Решение прямой геодезической задачи
Если расхождение в координатах не более 0,02 м, то находят средние значения координат X1 и Y1. |
