Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
7.1. Теоремы сложения вероятностей Теорема 7.1. (сложение вероятностей двух несовместных событий). суммы деклараций Определим вероятность Вероятность двух несовместных событий равна сумме вероятностей этих событий. 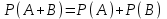 (6.4) (6.4)Теорема 7.2.(сложение вероятностей n несовместных событий). Вероятность суммы nнесовместных событий А1, А2, …, Аn равна сумме вероятностей этих событий: 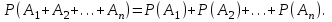 (6.5) (6.5)Следствие. Если события 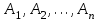 образуют полную группу несовместных событий, то сумма их вероятностей равна единице. образуют полную группу несовместных событий, то сумма их вероятностей равна единице. (6.6) (6.6)Следствие. Сумма вероятностей противоположных событий равна единице. 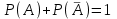 (6.7) (6.7)7.2. Условные вероятности. Теорема умножения вероятностей Определение. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет. Определение. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет. Определение. Вероятность события В, вычисленная при условии, что имело место событие А, называется условной вероятностью события В.  (6.8) (6.8)Теорема 7.3. (умножения вероятностей). Вероятность произведения двух событий (совместного появления этих событий) равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие уже наступило. 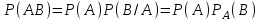 (6.9) (6.9)Определение независимых событий можно переформулировать следующим образом. Определение. Событие В не зависит от события А, если 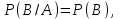 т.е. вероятность события В не зависит от того, произошло ли событие А. Свойство независимости событий: если вероятность события В не зависит от того, произошло ли событие А, то вероятность события А не зависит от события В, т.е. свойство независимости событий является взаимным. Отметим, что если А и В независимы, то независимы  и В, А и и В, А и 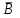 , ,  и и 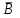 . .Следствие. Если события независимые, то вероятность произведения данных событий равна произведению вероятностей этих событий: 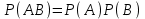 (6.10) (6.10)Для трех независимых событий А, В, С формула принимает вид 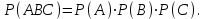 Теорема 7.4. (сложение вероятностей двух совместных событий). Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.  (6.11) (6.11)Из теоремы произведения вероятностей можно сделать вывод о вероятности появления хотя бы одного события. Вычисление вероятности суммы событий можно свести к вычислению вероятности произведения противоположных событий по формуле:  В частности, если события А1, А2, …, Аnнезависимы, то 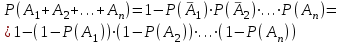 Если обозначить 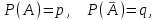  то формула примет вид 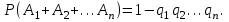 Если независимые события А1, А2, …, Аn имеют одинаковую вероятность, равную р, то вероятность появления хотя бы одного из этих событий выражается формулой  , где , где 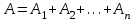 , q=1- p. , q=1- p.Пример 2. Вероятность нарушения таможенных правил участником ВЭД равна 1/6. Найти вероятность того, что при контроле трех участников появится хотя бы на одно нарушение. Решение. 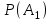 - вероятность нарушения таможенных правил участником ВЭД равна 1/6. Вероятность того, что не произойдет нарушение - - вероятность нарушения таможенных правил участником ВЭД равна 1/6. Вероятность того, что не произойдет нарушение -  . Вероятность того, что при контроле трех участников ВЭД не будет ни разу нарушений . Вероятность того, что при контроле трех участников ВЭД не будет ни разу нарушений 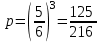 . .Вероятность того, что при контроле трех участников появится хотя бы на одно нарушение 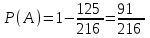 . .Пример 3. Проводится контроль партии товара. Вероятность нарушения таможенных правил вида А участником ВЭД равна 0,7, а для вида В – 0,8. Найти вероятность того, что при контроле партии нарушение появится только одно. Решение. Обозначим нарушения таможенных правил вида А – событие А, – событие В, А – событие  , не нарушение вида В – событие , не нарушение вида В – событие 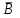 . .Вероятность того, что нарушения таможенных правил вида А произойдет, а нарушения таможенных правил вида В не произойдет. 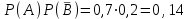 Вероятность того, что нарушения таможенных правил вида А не произойдет, а нарушения таможенных правил вида В произойдет.  Тогда вероятность того, что при контроле партии нарушение появится только одно равна  Тот же результат можно получить другим способом – находим вероятности того, что оба нарушения таможенных правил произойдут и оба не произойдут. Эти вероятности соответственно равны: 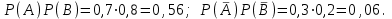 Тогда вероятность того, что при контроле партии нарушение появится только одно равна 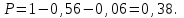 7.3. Формула полной вероятности. Формула Байеса. Пусть некоторое событие А может произойти вместе с одним из несовместных событий 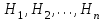 , составляющих полную группу событий. Пусть известны вероятности этих событий , составляющих полную группу событий. Пусть известны вероятности этих событий 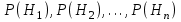 и условные вероятности наступления события А при наступлении событий Hi и условные вероятности наступления события А при наступлении событий Hi 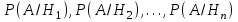 . .Теорема 7.5. Вероятность события А, которая может произойти лишь при условии появления одного из несовместных событий 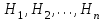 , образующих полную группу событий, равна сумме произведений вероятностей каждого из событий , образующих полную группу событий, равна сумме произведений вероятностей каждого из событий 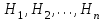 на соответствующие им условные вероятности наступления события А при данной гипотезе. на соответствующие им условные вероятности наступления события А при данной гипотезе.Р(А)= Р(Н1)· Р(А/ Н1) + Р(Н2 ) · Р(А/Н2) +…+ Р(Нn) · Р(А/Нn), (6.12) где Р(Н1) - вероятность события Н1, Р(Н2) - вероятность события Н2, Р(Нn) - вероятность события Нn, Р(А/Н1) - условная вероятность события А при условии, что произошло событие Н1, Р(А/Н2) - условная вероятность события А при условии, что произошло событие Н2, Р(А/Нn) - условная вероятность события А при условии, что произошло событие Нn. Равенство (6.12) называется формулой полной вероятности. События (гипотезы) Н1, Н2, … Нn попарно несовместны и образуют полную группу событий, поэтому Р(Н1 + Н2 + … + Нn) = 1. Пример 4. Вероятность выявления нарушений таможенных правил методом А равна 0,4, методом В – 0,6, методом С – 0,8. Найти вероятность того, что при контроле будет выявлено нарушение таможенных правил. Решение. Событие А– при контроле будет выявлено нарушение таможенных правил. Вероятность того, что будет применяться метод А, или В, или С равна  . .Вероятности того, что выявлено нарушение таможенных правил методом А, В, С. - для метода А Р(А/Н1)=0,4; - для метода В Р(А/Н2)=0,6; - для метода В Р(А/Н2)=0,8. Искомая вероятность равна: 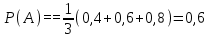 . .Формула Байеса (формула гипотез) Пусть имеется полная группа несовместных гипотез (событий) 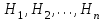 с известными вероятностями их наступления с известными вероятностями их наступления 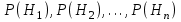 . В результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности . В результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности 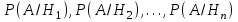 . .Требуется определить какие вероятности имеют гипотезы 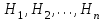 , когда событие А наступило, найти условные вероятности , когда событие А наступило, найти условные вероятности 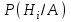 . .Теорема 7.6. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события. 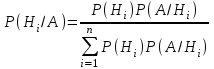 (7.13) (7.13)Эта формула называется формулой Байеса. Если до испытания все гипотезы равновероятны с вероятностью 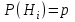 , то формула Бейеса принимает вид: , то формула Бейеса принимает вид: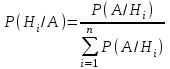 Формула Бейеса позволяет переоценить вероятности гипотез после того, как стал известен результат испытания, в итоге которого появилось событие А. Вероятности 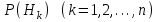 событий Н1, Н2, …, Нnдо опыта называются априорными вероятностями (от лат. apriori, что означает «сперва», т.е. в данном случае до того, как был произведен опыт). Вероятности событий Н1, Н2, …, Нnдо опыта называются априорными вероятностями (от лат. apriori, что означает «сперва», т.е. в данном случае до того, как был произведен опыт). Вероятности 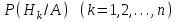 тех же событий называются апостериорными (от лат. aposteriori, что означает «после», т.е. в данном случае после опыта). тех же событий называются апостериорными (от лат. aposteriori, что означает «после», т.е. в данном случае после опыта).7.4. Независимые испытания. Формула Бернулли. Производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, вероятность появления одного события в каждом из испытаний не зависит от результатов остальных испытаний. Определение. Если проводятся повторные испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимыми относительно события А. Допустим, что событие А наступает в каждом испытании с вероятностью Р(А)=р. Определим вероятность Рт,п того, что в результате п испытаний событие А наступило ровно т раз. Эту вероятность можно вычислить, используя теоремы сложения и умножения вероятностей, как это делалось в рассмотренной выше теории. Однако, при достаточно большом количестве испытаний это приводит к очень большим вычислениям. Универсальный способ решения поставленной задачи предложил Якоб Бернулли (1654 – 1705) – швейцарский математик. Пусть в результате п независимых испытаний, проведенных в одинаковых условиях, событие А наступает с вероятностью Р(А) = р, а противоположное ему событие  с вероятностью с вероятностью 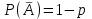 . .Обозначим Ai – наступление события А в испытании с номером i. Так как условия проведения опытов одинаковы, то эти вероятности равны. Если в результате п опытов событие А наступает ровно т раз, то остальные п-т раз это событие не наступает. Событие А может появиться т раз в п испытаниях в различных комбинациях, число которых равно количеству сочетаний из п элементов по т. Это количество сочетаний находится по формуле: 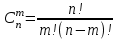 Вероятность каждой комбинации равна произведению вероятностей: 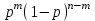 Применяя теорему сложения вероятностей несовместных событий, получаем формулу : 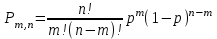 Формула Бернулли важна тем, что справедлива для любого количества независимых испытаний, т.е. того самого случая, в котором наиболее четко проявляются законы теории вероятностей. Теорема 7.7. (Бернулли). Вероятность того, что в n независимых повторных испытаниях, в каждом из которых вероятность появления события А равна р (0 < р < 1), событие А наступит ровно k раз (безразлично, в какой последовательности), равна:  (7.14) (7.14)Или  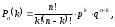 где где 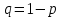 , ,k – число появлений события А в n независимых испытаниях. Следует помнить, что 0! = 1. Пример 5. Проводится контроль пяти партий товара. Вероятность нарушения в партии равна 0,4. Найти вероятность того, что выявлено не менее трех раз нарушений. Решение. Вероятность не менее трех нарушений складывается из вероятности пяти нарушений, четырех нарушений и трех нарушений. Т.к. нарушения независимы, то можно применить формулу Бернулли вероятности того, что в т испытаниях событие в вероятностью р наступает ровно п раз. 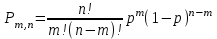 В случае пяти нарушений из пяти возможных: 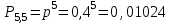 Четыре нарушения из пяти партий:  Три нарушения из пяти:  Окончательно, получаем вероятность не менее трех нарушений при контроле пяти партий: 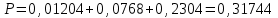 Удобно использовать следующие схемы для вычисления вероятности того, что событие А наступит: а) менее k раз 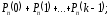 б) более k раз  в) не менее k раз 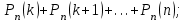 г) не более k раз 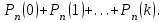 Рассмотрим теперь вероятность того, что событие появится от k1 до k2 раз. По теореме сложения для несовместных событий, вероятность  того, что событие А появилось в n испытаниях от k1до k2разравна того, что событие А появилось в n испытаниях от k1до k2разравна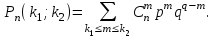 (7.15) (7.15)7.5. Локальная и интегральная теоремы Лапласа. Теорема Пуассона. Однако, если число испытаний достаточно велико, то использовать формулу Бернулли нецелесообразно в силу необходимости выполнения громоздких вычислений. Применяют локальную теорему Муавра – Лапласа, дающую асимптотическую формулу, которая позволяет вычислить вероятность приближенно. Теорема 7.8. (Локальная теорема Муавра – Лапласа.) Если вероятность наступления события А в каждом из n независимых испытаниях равна р и отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность 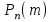 того, что в n испытаниях событие А наступит m раз, приближенно равна значению функции того, что в n испытаниях событие А наступит m раз, приближенно равна значению функции 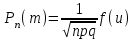 , где , где 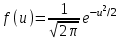 , ,   , ,  . (7.16) . (7.16)Чем больше число испытаний n, тем точнее результат вычисления вероятности. Значение функции 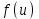 представлено в таблице функции Лапласа. При использовании этой таблицы следует помнить, что функция представлено в таблице функции Лапласа. При использовании этой таблицы следует помнить, что функция 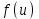 – четная, т.е. – четная, т.е. 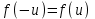 . Применение локальной теоремы Муавра–Лапласа, возможно, если n иметь порядок не менее нескольких десятков, а лучше нескольких сотен, а произведение np>10. . Применение локальной теоремы Муавра–Лапласа, возможно, если n иметь порядок не менее нескольких десятков, а лучше нескольких сотен, а произведение np>10.Если вероятность события р (или q) в отдельном испытании близка к нулю (такие события называются редкими), то даже при большом числе испытаний n, но небольшой величине произведения np (не больше 10), вероятности Рn (m), полученные по теореме Муавра– Лапласа, недостаточно близки к их истинным значениям. В таких случаях применяют другую асимптотическую формулу – формулу Пуассона. Теорема 7.9. (Пуассона.) Если вероятность наступления события А в каждом испытании постоянна, но близка к нулю, число независимых испытаний п достаточно велико, а произведениеnр равно λ, то вероятность Рn (m) того, что вnнезависимых испытаниях событиеА наступитmраз, приближенно равна 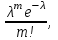 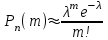 . (7.17) . (7.17)Формула называется формулой Пуассона. Условия теоремы требуют, чтобы вероятность события р была мала, а число испытаний n велико. Обычно указанную формулу используют, когда n ≥10, лучше n ≥ 100, а пр ≤ 10. При больших п эта формула (7.15) приводит к громоздким вычислениям. В этих случаях применяют интегральную теорему Муавра–Лапласа. Теорема 7.10. (Интегральная теорема Муавра–Лапласа.) Если вероятность р наступления события А в каждом испытании отлична от нуля и единицы, то вероятность того, что событие А появится в п независимых испытаниях от k1до k2 раз, равна  , где , где 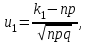  (7.18) (7.18)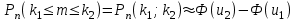 Для применения этой формулы n должно иметь порядок не менее нескольких десятков (лучше сотен), а np>10. Преобразуем интеграл в правой части так, чтобы было можно использовать интегральную функцию Лапласа Ф(и). 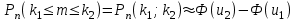 где 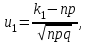 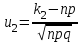 , ,  Значения функции Ф(и) приведены в таблице функции Лапласа. Пример 6. Вероятность того, что партия товара выпущенная под заявленную таможенную процедуру не содержит нарушений таможенных правил, равна 0,9. Найти вероятность того, что из 400 выпущенных партий 356 не содержит нарушений таможенных правил. Решение. В данной формуле соблюдены все условия локальной теоремы Муавра–Лапласа. Согласно условию примера, n = 400, m = 356, p = 0,9, q = 0,1. По формуле находим 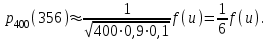 Далее из условия следует, что 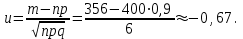 Учитывая, что 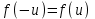 , находим f(-0,67)= f(0,67)=0,3188. Искомая вероятность , находим f(-0,67)= f(0,67)=0,3188. Искомая вероятность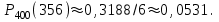 Пример 7. Известно, что при таможенном контроле выявляется в 10% нарушения. На контроль отобрано 625 изделий. Какова вероятность того, что среди отобранных не менее 550 и не более 575 партий не содержат нарушения? Решение. Условия данного примера соответствуют условию интегральной теоремы Муавра–Лапласа. По условию, n=625; p=0,9; k1=550; k2=575. Искомую вероятность находим по формуле. Имеем  Пример 8. Вероятность того, что при оформлении одной таможенной декларации допускается ошибка по определению таможенной процедуры, равна 0,002. В течение месяца таможней оформлено 500 деклараций. Определить вероятность того, что среди оформленных деклараций будут декларации с ошибками в количестве, равном: а) трем; б) менее трех. Решение. Число испытаний n велико, а вероятность появления события А в одном испытании р = 0,002 мала, поэтому для определения искомой вероятности используем формулу Пуассона 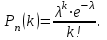 Находим параметр : = np = 500 ∙ 0,002 = 1. 2. Определим вероятность того, с ошибками будет оформлено ровно три декларации (k= 3):  3. того, что с ошибками будет оформлено менее трех: 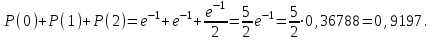 Глава 8. Случайные величины Одним из важнейших понятий теории вероятностей является понятие случайной величины 8.1. Понятие случайной величины. Определение. Случайной величиной называется величина, которая в результате опыта принимает одно и только одно из возможных своих значений, зависящее от случайных причин, которые заранее не могут быть учтены (какое именно значение – заранее неизвестное). Например, число деклараций контролируемых в течении месяца на таможенном посту. Объемы таможенных платежей, собираемых на таможне в течении месяца. Действительно, эти величины зависят не только от ставки таможенной пошлины, но и от многих других причин курса валют, объемов поставок и т. д., которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а, b). Мы будем далее обозначать случайные величины прописными буквами X, У, Zа их возможные значения— соответствующими строчными буквами х, у, z. Например, если случайная величина X имеет три возможных значения, то они будут обозначены так: х1, х2, х3. Различают случайные величины, принимающие лишь отдельные, изолированные значения и случайные величины, возможные значения которых сплошь заполняют некоторый промежуток. Случайные величины можно разделить на две категории. Определение. Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные изолированные значения с некоторой вероятностью. Определение. Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка. Очевидно, что число возможных значений непрерывной случайной величины бесконечно. 8.2. Способы задания случайной величины Для задания случайной величины недостаточно просто указать ее значение, необходимо также указать вероятность этого значения. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретной случайной величины. Закон распределения дискретной случайной величины может быть задан аналитически, в виде таблицы или графически. Таблица соответствия значений дискретной случайной величины и их вероятностей называется рядом распределения. При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:
В одном испытании случайная величина принимает одно и только одно возможное значение, события Х=х1, Х=х2, ..., Х=хп образуют полную группу событий; следовательно, сумма вероятностей этих событий равна единице: 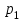 + +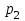 +…+ +…+ =1. =1.Графическое представление этой таблицы называется многоугольником распределения. В целях наглядности представления закона распределения дискретной случайной величины используют график. Для чего в прямоугольной системе координат строят точки ( 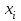 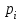 ). а затем соединяют их последовательно отрезками прямых. Полученную фигуру называют многоугольником распределения. ). а затем соединяют их последовательно отрезками прямых. Полученную фигуру называют многоугольником распределения. Определение. Многоугольником распределения называется ломанная линия, соединяющая последовательно точки с координатами ( 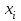 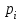 ). ).Пример 1. Дискретная случайная величина Х имеет закон распределения:
Чему равна вероятность р4 = Р (Х = 0,8)? Построить многоугольник распределения. Решение. 1. Поскольку должно выполняться равенство р1 +р2 +р3 + р4 + р5 = 1,то р4 =1 – (р1 +р2 +р3 + р5) = 1 – (0,1 + 0,2 + 0,4 + +0,1)= 1 – 0,8 = 0,2, р4= 0,2. 2. По данным таблицы строится многоугольник распределения  Рисунок 8.1. Многоугольник распределения В прямоугольной системе координат строим точки М1(0,2; 0,1), М2(0,4; 0,2), М3(0,6; 0,4), М4(0,8; 0,2), М5(1; 0,1); соединяем эти точки отрезками прямых (рис.1). Линия М1М2М3М4М5 является многоугольником распределения дискретной случайной величины. Функция распределения случайной величины Определение. Функцией распределения случайной величины называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х:  (8.1) (8.1)Функцию распределения также называют интегральной функцией распределения. Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения. Для дискретной случайной величины функция распределения согласно теореме сложения вероятностей можно представить в таком виде:  Функция распределения дискретной случайной величины Х , ряд распределения которой представлен в таблице
имеет вид: F 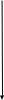 (x) (x)   1 1      0 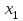 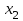 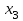 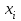 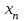 х хРисунок 8.2. Функция распределения дискретной случайной величины. Построим теперь функцию распределения случайной величины Х, ряд распределения которой представлен в таблице: при 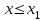 получаем получаем 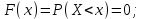 при 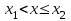 получаем получаем 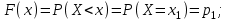 при 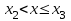 получаем получаем 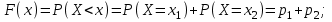 при 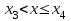 получаем получаем 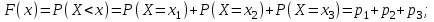 ……………………………………………. при 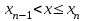 получаем получаем 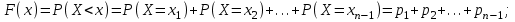 при 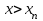 получаем получаем  Следует заметить, что функция распределения дискретной случайной величины Х разрывна и возрастает скачками при переходе через каждое значение хi. Пример 2. В поставке из восемь партий товаров, из которых пять с нарушениями таможенных правил. Наудачу взяты четыре партии. Построить функцию распределения числа партий с нарушениями таможенных правил среди отобранных. Решение. Случайная величина Х- число партий с нарушениями таможенных правил среди отобранных. Эта случайная величина может принимать значения 1, 2, 3 или 4. Для определения вероятности появления конкретного числа партий с нарушениями таможенных правил 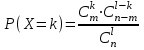 , где , гдеn– число партий товара, l– число отобранных партий, m-число партий с нарушениями таможенных правил, k - число партий с нарушениями таможенных правил среди отобранных.  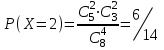 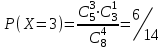 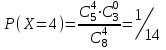 . .Закон распределения представим в виде таблицы:
|