Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
Глава 2. Решение систем линейных уравнений 2.1. Основные принятия системы линейных уравнений Определение.Системой линейных уравнений , состоящей из m уравнений с n неизвестными 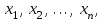 называется система вида называется система вида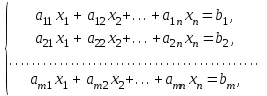 (2.1) (2.1)где числа 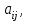 (i=1,2,…, m; j=1,2,…,n) называются коэффициентами при неизвестных, числа (i=1,2,…, m; j=1,2,…,n) называются коэффициентами при неизвестных, числа 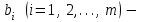 свободными членами. Введем матрицы: свободными членами. Введем матрицы: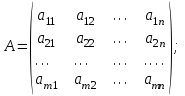  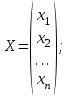 где A- матрица коэффициентов при переменных, или матрица системы; В- матрица-столбец свободных членов, X- матрица- столбец переменныx. После этого система (2.1) записывается в виде одного матричного уравнения AX = B с неизвестным столбцом X. Определение. Совокупность n чисел α1, α2, … , αn называется решением системы(2.1), если после замены неизвестных x1, x2 ,…, xn числами α1, α2, … , αn соответственно каждое из уравнений системы обращается в верное равенство. Определение. Система, не имеющая ни одного решения, называется несовместной. Система, имеющая хотя бы одно решение, называется совместной. Для каждой системы уравнений можно говорить о множестве всех решений. Для несовместной системы множество решений – пустое множество. Решить систему уравнений – это значит найти множество ее решений. Для этого достаточно решить три задачи. Задача 1. Выяснить, совместна система или несовместна. Задача 2. Если система совместна, то определить количество ее решений. Задача 3. Найти все решения системы. 2.2. Решение системы линейных уравнений с помощью обратной матрицы и по формулам Крамера Рассмотрим систему уравнений (2.1), у которой число уравнений равно числу неизвестных, т.е. 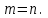 У такой системы матрица системы A- квадратная матрица. У такой системы матрица системы A- квадратная матрица.Определитель 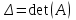 называется определителем системы. называется определителем системы.Рассмотрим два основных метода решения систем уравнений, у которых число уравнений равно числу неизвестных и 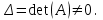 Будут указаны явные формулы для нахождения единственного решения системы. Метод Крамера решения системы линейных уравнений (СЛУ). Случай 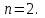 Рассматривается система линейных уравнений: Рассматривается система линейных уравнений: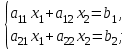 (2.2 ) (2.2 )x1, x2-неизвестные, 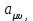  - заданы; - заданы;  -называются коэффициентами системы, -называются коэффициентами системы,  -свободными членами. -свободными членами.Вычисляются определители  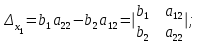 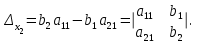 При решении системы уравнений (2.2) возможны три случая. 1.Определитель системы  не равен нулю. Тогда система имеет единственное решение, определяемое формулами Крамера: не равен нулю. Тогда система имеет единственное решение, определяемое формулами Крамера: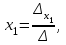 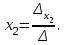 2.Если Δ=0 и хотя бы один из определителей 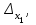 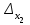 отличен от нуля, то система не имеет решений. отличен от нуля, то система не имеет решений.3.Если  то система имеет бесконечно много решений.Пример 1. Решить системы уравнений: то система имеет бесконечно много решений.Пример 1. Решить системы уравнений: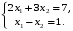 Решение. 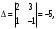 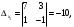  Система имеет единственное решение:  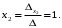 Правило Крамера. Мы уже рассматривали правило Крамера для решения системы двух уравнений с двумя неизвестными. Обобщим его на случаи любого числа неизвестных. Теорема Крамера 2.1. Пусть дана система n линейных уравнений с n неизвестными AX=B. Если |A|≠0, то система имеет единственное решение: 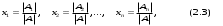 где Ai - матрица, полученная из A заменой её i-го столбца столбцом свободных членов B (i=1,2,…, n). Формулы (2.3) называются формулами Крамера, а правило решения систем с помощью этих формул- правилом Крамера. Расмотрим систему трех уравнений с тремя неизвестными  Вычисляются определители 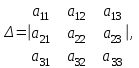    Если 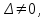  то система имеет единственное решение то система имеет единственное решение  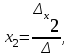  2.Если Δ=0, но хотя бы один из определителей 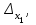   отличен от нуля, то система не имеет решений. отличен от нуля, то система не имеет решений. 3.Если  , то возможны случаи: , то возможны случаи: а) система не имеет решений; б) система имеет бесконечно много решений. Пример 2. Решить систему уравнений с помощью правила Крамера: 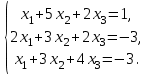 Решение. Имеем: 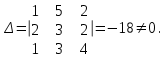 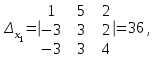   По формулам Крамера :    2.3. Метод обратной матрицы решения СЛУ. Запишем систему (2.1) в матричной форме AX=B. Тогда столбец неизвестных X=A-1B. (2.4) Пример 3. Решить систему уравнений  Решение. Методобратной матрицы. Введем матрицы: 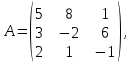  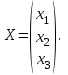 Вычислим определитель системы  Так как 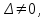 то существует то существует 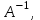 и решение системы может быть найдено по формуле X=A-1B. и решение системы может быть найдено по формуле X=A-1B. Транспонируем матрицу A. 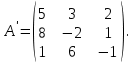 Составим присоединенную матрицу из алгебраических дополнений к элементам транспонированной матрицы: 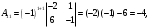  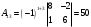 , , 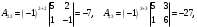 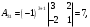  Тогда  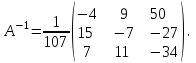 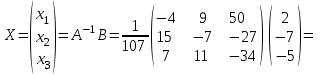  Таким образом,  Теорема о равносильности систем при элементарных преобразованиях Теорема 2.2. (о равносильности систем при элементарных преобразованиях) При элементарных преобразованиях строк первых четырех типов линейные системы остаются равносильными. Рассмотрим элементарные преобразования каждого типа по отдельности. Если система линейных уравнений получена из исходной системы элементарными преобразованиями первого типа, т.е. изменен порядок уравнений в системе, то решения системы не изменятся. Если система линейных уравнений получена из исходной системы элементарными преобразованиями второго типа, т.е. одно из уравнений умножено на число a≠0, это не примет к изменению решений системы. Если система линейных уравнений получена из исходной системы элементарными преобразованиями третьего типа, т.е. одно из уравнений представляет собой сумму двух уравнений, одно из которых предварительно умножено на число λ, это также не приведет к изменению решений системы. Действительно, пусть 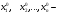 решение системы уравнений. Тогда уравнения с произвольными номерами i и j решение системы уравнений. Тогда уравнения с произвольными номерами i и j При подстановке чисел 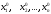 обратятся в тождества. Сложим оба уравнения, предварительно умножив первое из них на число λ: обратятся в тождества. Сложим оба уравнения, предварительно умножив первое из них на число λ: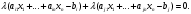 Подставив сюда числа 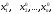 получим λ∙0+0=0. получим λ∙0+0=0.Если система линейных уравнений получена из исходной системы элементарными преобразованиями четвертого типа, т.е. одно из уравнений, содержащее нулевые коэффициенты и нулевой свободный член, вычеркнуто, это очевидно, не изменит решений системы. 2.4. Метод Гаусса Рассмотрим решение системы  (i=1,2,…,m). (i=1,2,…,m).m линейных уравнений с n переменными в общем виде. Метод Гаусса (Гаусс Фридрих Карл (1777-1855)- немецкий математик) – метод последовательного исключения переменных заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные. Пусть для определенности в системе (2.1) a11 ≠ 0 (если a11 =0, то переставим на первое место другое уравнение с ненулевым первым коэффициентом). Для системы уравнений (2.1) образуем расширенную матрицу  Посредством элементарных преобразований приведем расширенную матрицу к ступенчатому виду  Рассмотрим различные случаи: br+1 ≠0. Расширенная матрица имеет вид флажка. Тогда система уравнений несовместна. Действительно, уравнение с номером r+1 содержит нулевые коэффициенты перед неизвестными, тогда как свободный член отличен от нуля. Пусть далее br+1=0. Число неизвестных n и число уравнений r совпадают. Расширенная матрица примет треугольный вид. 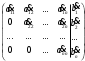 Система уравнений, соответствующая этой матрице, имеет вид  Из последнего уравнения определяется неизвестная величина xn. Подставляем ее в предыдущее уравнение с номером n-1 и находим xn-1. Продолжая этот процесс, находим неизвестные со все меньшими номерами. Наконец, подставив найденные значения неизвестных x1, x2, … , xn в первое уравнение, найдем величину x1. Итак, при r=n система совместна и имеет единственное решение. Число неизвестныхnбольше числа уравненийr. Вид расширенной матрицы - трапеция. Последнее уравнение содержит переменные xr , xr+1 , …, xn. Выразим в этом уравнении переменную xr через остальные неизвестные и подставим в уравнение с номером r-1. Найдем переменную xr-1, которая будет выражена через те же неизвестные xr+1 , …, xn. Результат подставим в уравнение с номером r-2 и т.д. Таким образом мы можем определить значения переменных xr , xr-1 , …, x1 через неизвестные xr+1 , xr+2 , …, xn  Придавая неизвестнымxr+1 , …, xnпроизвольные значения получаем бесконечное множество решений системы уравнений. Пример 4. Решить систему уравнений методом Гаусса  Решение. Способ 1 (без расширенных матриц). Первое уравнение оставляем без изменений, а из остальных трех уравнений исключим x1 . Для этого первое уравнение, умноженное на 3 и 2, вычтем из второго и третьего соответственно, далее из четвертого уравнения вычтем первое, в результате получим  Мы получили систему уравнений, в которой первое уравнение содержит все неизвестные, а в остальных нет неизвестного x1 Так называемый первый шаг метода закончен. Теперь первое и второе уравнения оставим без изменения, а из третьего и четвертого уравнений исключим x2. Для этого нужно второе уравнение умножить на ¼ и результат сложить с третьим и четвертым: 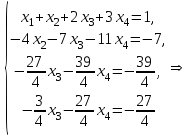 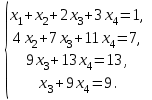 Второй шаг метода закончен. Исключим из четвертого уравнения неизвестной x3 , для этого третье умножим на 1/9 и результат вычтем из четвертого уравнения, получим 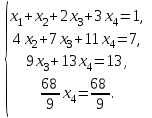 Третий шаг метода закончен и закончен так называемый прямой ход метода. Обратным ходом получаем x4 =1; 9x3 +13·1=13, x3 =0; 4x2 +7·0+11·1=7, x2 = - 1; x1 -1+2·0+3·1=1, x1=-1. Отметим, что в ходе применения метода Гаусса может встретиться уравнение вида 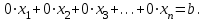 При b≠0 система несовместна, так как этому уравнению не удовлетворяют никакие значения неизвестных. При b=0 уравнение является тождеством и ему удовлетворяют любые значения неизвестных. Это уравнение (тождество) можно удалить из системы. При b≠0 система несовместна, так как этому уравнению не удовлетворяют никакие значения неизвестных. При b=0 уравнение является тождеством и ему удовлетворяют любые значения неизвестных. Это уравнение (тождество) можно удалить из системы.Пример 5. Решить систему уравнений 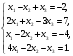 Решение. Способ 2 (с помощью расширенных матриц) Выпишем расширенную матрицу системы: 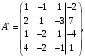 и подвергнем ее элементарным преобразованиям. Умножим первую строку на числа 2, 1, 4 и вычтем ее последовательно из второй, третьей и четвертой срок, после чего поменяем местами вторую и третью строки, получим: 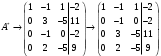 Умножим теперь вторую строку на числа 3, 2 и сложим ее последовательно с третьей и четвертой строками, получим: 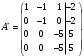 Наконец, умножим вторую строку на -1, третью строку вычтем из четвертой, после чего умножим третью строку на -1/5, получим: 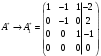 Полученная расширенная матрица 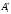 соответствует системе соответствует системе 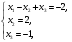 которая эквивалентна исходной системе. Подставляя x2 и x3 в первое уравнение, находим x1=1. Итак, решением системы уравнений является тройка чисел 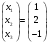 Теорема 2.5. Кронекера-Капелли. Для того, чтобы система n-линейных уравнений имела решения, необходимо и достаточно, чтобы ранг r матрицы системы A был равен рангу расширенной матрицы этой системы  т.е. т.е.  Если 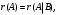 причем причем 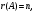 система имеет единственноерешение. система имеет единственноерешение.Если 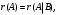 причем причем 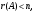 система имеет бесконечное множество решений, которое может быть определенным образом структурировано. r переменных могут быть найдены через остальные n-r переменных. Эти r переменных называются базисными, остальные n-r переменных называются свободными. Переменная xiможет быть включена в число базисных переменных, если определитель матрицы из коэффициентов при них отличен от нуля. Решение системы уравнений, в котором n-r свободных переменных кладутся равными нулю, называется базисным. система имеет бесконечное множество решений, которое может быть определенным образом структурировано. r переменных могут быть найдены через остальные n-r переменных. Эти r переменных называются базисными, остальные n-r переменных называются свободными. Переменная xiможет быть включена в число базисных переменных, если определитель матрицы из коэффициентов при них отличен от нуля. Решение системы уравнений, в котором n-r свободных переменных кладутся равными нулю, называется базисным.В системе (2.5') базисным решением является совокупность переменных: 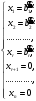 или в матричной форме  2.6) 2.6)В сокращенной матричной форме базисное решение 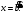 (2.6') (2.6')Базисное решение является частным решением системы (2. 5). Пример 6. Найти какое –либо базисное решение системы уравнений 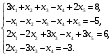 Решение. Найдем расширенной матрицы системы:  Минор в квадратных скобках, составленный из коэффициентов при переменных x1 , x2 , x3 ,отличен от нуля. Ранг матрицы коэффициентов равен трем, ранг расширенной матрицы - также три. Следовательно, по теореме Кронекера - Капелли система имеет решения. Найдем те из них, которые называются базисными. Положим переменные x1 , x2 , x3 основными, переменные x4, x5 – свободными и равными нулю. Тогда получим систему 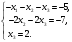 Решая ее, найдем базисное решение  Пример 7. Решить систему уравнений  Решение. Составим расширенную матрицу и применим метод Гаусса: 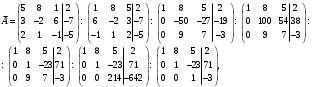 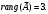 Так как первые три столбцов матрицы 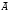 образуют матрицу A и при элементарных преобразованиях последний столбец матрицы образуют матрицу A и при элементарных преобразованиях последний столбец матрицы 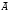 остался на месте, то остался на месте, то  Таким образом,  следовательно, система совместна. Количество неизвестных n=3 совпадает с общим значением рангов матриц A и следовательно, система совместна. Количество неизвестных n=3 совпадает с общим значением рангов матриц A и  следовательно , система имеет единственное решение. Для его нахождения перейдем от преобразованной расширенной матрицы к системе уравнений следовательно , система имеет единственное решение. Для его нахождения перейдем от преобразованной расширенной матрицы к системе уравнений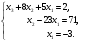 Найдем из этой системы неизвестные. 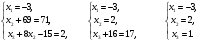 2.6. Однородные СЛУ и их свойства. Система линейных уравнений называется однородной, если все свободные члены системы равны нулю 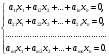 ( 2.7) ( 2.7)В матричном виде систему можно записать так: A∙X=0, где 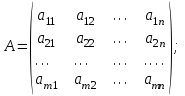  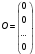 Свойства однородной системы линейных уравнений Рассмотрим свойства однородной системы линейных уравнений. 1) Однородная система всегда совместна, так как всегда имеет по крайней мере нулевое решение. 2) Для существования ненулевых решения ранг матрицы коэффициентов должен быть меньше числа переменных r 3) Если матрица –столбец (вектор) 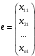 есть решение системы (2.7), то и столбец есть решение системы (2.7), то и столбец  также является решением системы. также является решением системы.Пусть e– решением системы. Тогда матричное уравнение при подстановке 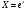 обращается в тождество обращается в тождество 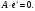 Действительно, найдем произведение матриц Aи λe A∙(λe)=λ∙(A∙e)=λ∙0=0. Отсюда столбец  также является решением матричного уравнения. также является решением матричного уравнения.4).Если матрицы-столбцы 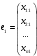 и и  есть решения системы (2,7) т.е. есть решения системы (2,7) т.е.  и и 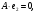 то и столбец e= λ1e1+ λ2 e2 , где λ1 , λ2 –произвольные числа, также является решением системы то и столбец e= λ1e1+ λ2 e2 , где λ1 , λ2 –произвольные числа, также является решением системы  Следовательно, всякая линейная комбинация решений однородной системы линейных уравнений также является решением этой системы. Заметим, что среди решений однородной системы выделяются решения, которые можно назвать главными решениями, через них выражаются другие решения. Попробуем разобраться в этом и выделить фундаментальные решения. Фундаментальная система решения однородной СЛУ. Решение e1, e2, …, ep однородной системы называются линейно независимыми, если линейная комбинация этих решений λ1e1 + λ2e2 +…+ λpep равна нулевому столбцу только при условии λ1 = λ2 =…,= λp =0. Построим матрицу решений, расположив матрицы-столбцы решений по столбцам новой матрицы. В соответствии с теоремой о ранге матрицы, ранг новой матрицы будет численно равен числу столбцов новой матрицы, т.е. числу линейно независимых решений системы. Определение. Совокупность линейно независимых решений e1 , e2 ,… ep однородной системы уравнений называется фундаментальной, если общее решение системы является линейной комбинацией решений e1 , e2 ,… ep Теорема 2.8. (о фундаментальных решениях однородной системы) Если ранг r матрицы коэффициентов при переменных однородной системы уравнений меньше числа переменных n, то: 1) существует совокупность линейно независимых решений системы: 2) число линейно независимых решений равно n-r; 3) любое решение системы можно представить в виде совокупности этих независимых решений, т.е. в виде линейной комбинации фундаментального набора решений. Решим систему (2.7) в общем виде. Выпишем матрицу коэффициентов и приведем ее элементарными преобразованиями к ступенчатому виду 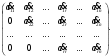 Базисными возьмем переменные x1, x2 , …, xr , тогда свободными переменными станут xr+1, xr+2, …, xn . Если в процессе приведения матрицы коэффициентов к ступенчатому виду пришлось поменять столбцы, можно перенумеровать переменные. Для свободных переменных введем обозначения xr+1 =с1, xr+2=с2, …, xn=сn-r. Далее, действуя по методу Гаусса, из последнего уравнения с номером r найдем величину xr , которую подставим в предыдущее уравнение с номером r-1. Из уравнения с номером найдем величину xr-1, которую подставим в уравнение с номером r-2, и т.д. В результате получим решение системы в общем виде:  Здесь коэффициенты xij получены в результате преобразований: i=1, … , r, j=1, … , n-r. Запишем решения в матричной форме: 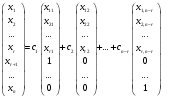 (2.8) (2.8)или в сокращенной матричной форме: x=c1e1+ c2e2 +…+ crer, (2.8') где x, e2 , e2 ,…, er -соответствующие матрицы-столбцы (векторы). Величины c1 , c2, …, cn-r могут принимать любые действительные значения. Положим c1 = 1 , c2 = 0, … , cn-r= 0. Тогда частное решение системы. 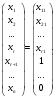 Придавая величинам c1 , c2, …, cn-r другие значения, убедимся, что матрицы-столбцы  также являются решениями системы однородных уравнений. Число этих столбцов равно n-r. Составим из них матрицу, записав более подробно последние n-r строк:  Матрица содержит минор Mn-r порядка n-r, по главной диагонали которого стоят единицы, остальные элементы равны нулю. Очевидно, Mn-r=1. Следовательно, ранг матрицы равен n-r. Но тогда эти столбцы линейно независимы. Мы доказали, что матрицы - столбцы, стоящие в правой части выражения (2.7), являются решениями однородной системы, они линейно независимы. Их число равно n-r. Общее решение (2.8) однородной системы получено в виде линейной комбинации этих независимых решений. Теорема доказана. Замечание1. Базисными переменными мы выбрали неизвестные x1, x2 , …, xr. В качестве базисных можно выбрать любой набор из rпеременных при условии, что определитель матрицы из коэффициентов при них отличен от нуля. Количество способов выбора таких r переменных из их общего числа не превышает величины  Отсюда следует, что число фундаментальных наборов решений (ФНР) ограничено. Замечание 2. Для нахождения множества решений однородной системы достаточно найти какой-нибудь ФНР системы и составить его линейную комбинацию. Замечание 3. Любая однородная система уравнений, имеющая ненулевые решения, обладает ФНР. Замечание 4. Если матрицы-столбцы в выражении (2.8) не содержат иррациональностей, подбором коэффициентов c1 , c2, …, cn-r всегда можно создать ФНР, все элементы которого будут целыми числами. Пример 8. Решить систему однородных уравнений, выделив какой -либо ФНР 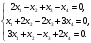 Решение. Запишем матрицу коэффициентов и, совершая элементарные преобразования со строками, приведем ее к ступенчатому виду 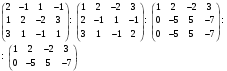 Ранг матрицы r=2. Вернемся к системе уравнений: 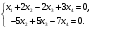 (2.9) (2.9)Возьмем базисными переменными x1, x2, тогда свободными останутся x3 , x4. Найдем x1, x2, и запишем решения в удобной для дальнейшей записи форме  В матричном виде решение системы можно записать так: 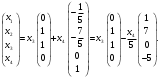 Обозначим коэффициенты перед столбцами в правой части: 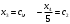 и запишем общее решение системы еще раз: 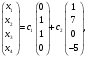 где где  Задавая коэффициентам c1, c2 произвольные значения, получаем совокупность всех решений системы. Столбцы 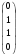 и и 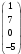 линейно независимы и представляют набор из двух фундаментальных решений (ФНР), через которые выражаются все остальные решения системы. линейно независимы и представляют набор из двух фундаментальных решений (ФНР), через которые выражаются все остальные решения системы.Другой подход к форме записи заключается в составлении таблицы для системы (2.9):
Заполняем таблицу, задавая значения свободным переменным коэффициенты x3, x4. Рассчитываем значения переменных x1,x2. Подбираем коэффициенты α1, α2 так, чтобы при умножении их на элементы соответствующей строки получались целые числа. Пусть α1 =1, α2 =-5. Решение системы запишем в виде (2.10) Общее решение системы неоднородных линейных уравнений. Теорема 2.9. (общем решении системы неоднородных уравнений) Общее решение системы линейных уравнений с n переменными равно сумме общего решения соответствующей ей системы однородных линейных уравнений и некоторого частного решения исходной системы. Для системы m линейных уравнений с n переменными  запишем расширенную матицу  Используя элементарные преобразования, приведем ее к ступенчатому виду  Убедившись, что система имеет решения, методом Гаусса найдем последовательно переменные xr, xr-1 , …, x1 , выражение через свободные переменные xr+1, xr+2 , …, xn.. .Для свободных переменных введем обозначения xr+1=с2, xr+2 =с2, …, xn =сn-r. В результате получим решение системы в общем виде: 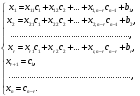 Коэффициенты xij, 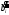 получены в результате преобразований, i=1, …, r, j=1,…, n-r. Величины c1 , c2, …, cn-r могут принимать любые действительные значения. Запишем решения в матричной форме: получены в результате преобразований, i=1, …, r, j=1,…, n-r. Величины c1 , c2, …, cn-r могут принимать любые действительные значения. Запишем решения в матричной форме: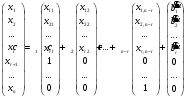 или в сокращенной матрице форме: 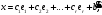 где 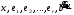 соответствующие матрицы-столбцы (векторы). Линейная комбинация соответствующие матрицы-столбцы (векторы). Линейная комбинация 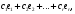 есть общее решение (2.8) системы однородных линейных уравнений, вектор есть общее решение (2.8) системы однородных линейных уравнений, вектор 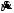 частное решение (2,6) исходной системы. В сокращенной матричной форме эти решения представлены формулами (2.8') и (2.6'). частное решение (2,6) исходной системы. В сокращенной матричной форме эти решения представлены формулами (2.8') и (2.6'). |