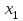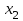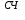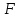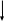Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
Глава 3. Модель Леонтьева многоотраслевой экономики Соотношения между выпуском продукции отдельных стран позволяют экономике мирового хозяйства функционировать сбалансированно. Для этих целей разрабатываются модели международной торговли (обмена). В моделях микроэкономики (многоотраслевой экономики) описываются обменные процессы, возникающие между потребителями и производителями продукции. Модели связи между видами экономической деятельности (отраслями экономики) через выпуск и потребление продукции разного вида были представлены американским экономистом В. Леонтьевым в 1936 году. Теоретической основой этих моделей является аппарат матричного анализа. 3.1. Балансовые соотношения В простейших моделях в производственной сфере представляется n видов экономической деятельности, каждый из которых производит определенный однородный продукт. Для обеспечения производства каждая организация нуждается в продукции других видов экономической деятельности (производственное потребление). Процесс производства описывается за определенный период (например, год). Вводятся следующие обозначения: 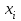 . — общий объем (валовой выпуск) продукции i-го вида экономической деятельности; . — общий объем (валовой выпуск) продукции i-го вида экономической деятельности;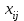 . — объем продукции i-го вида экономической деятельности (производителя), потребляемый j-м потребителем для производства объема продукции . — объем продукции i-го вида экономической деятельности (производителя), потребляемый j-м потребителем для производства объема продукции 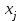 ; ;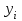 — объем продукции i-го производителя , предназначенный для реализации (потребления) в непроизводственной сфере (продукт конечного потребления). — объем продукции i-го производителя , предназначенный для реализации (потребления) в непроизводственной сфере (продукт конечного потребления). Продукт конечного потребления может включать личное потребление граждан, содержание государственных институтов, удовлетворение общественных потребностей и другое. Балансовый принцип связи заключается в том, что валовой выпуск i-го производителя должен быть равен сумме объемов потребления в производственной и непроизводственной сферах. В простейших линейных моделях балансовые соотношения имеют вид 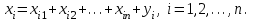 (3.1) (3.1)Уравнения 4.1 называются соотношениями баланса. Так единицы измерения объема выпускаемой продукции могут быть различны, то при составлении балансовых соотношений используется стоимостный баланс. Коэффициенты прямых и полных материальных затрат. Матрица прямых затрат В. Леонтьевым, на основании анализа экономики США, была выявлена следующая закономерность: отношение объема потребления продукции i-го производителя j-м потребителем 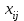 к объему производства продукции j-м потребителем к объему производства продукции j-м потребителем 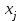 в течение длительного времени (величины в течение длительного времени (величины 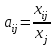 ) меняются незначительно и может рассматриваться как постоянные числа. ) меняются незначительно и может рассматриваться как постоянные числа. Это объясняется тем, что технология производства в течение некоторого времени остается на одном и том же уровне, и, следовательно, объем использования j-м потребителем продукции i –го производителя для производства своей продукции объема 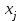 есть технологическая константа. есть технологическая константа.Следует, что для выпуска продукции j-м производителем объема 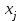 необходимо использовать продукцию i-й производителя объема необходимо использовать продукцию i-й производителя объема 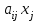 , где , где 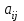 — постоянное число. — постоянное число. При данном условии технология производства принимается линейной, а само это допущение называется гипотезой линейности. Определение. Число 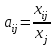 , называются коэффициентами прямых затрат. , называются коэффициентами прямых затрат. Согласно гипотезе линейности, 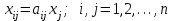 . (3.2) . (3.2)Перепишем уравнения 4.2 в виде системы уравнений: 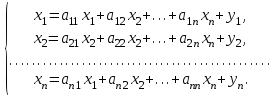 (3.3) (3.3)Обозначим через: 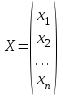 – вектор-столбец объема произведенной продукции (вектор валового выпуска); – вектор-столбец объема произведенной продукции (вектор валового выпуска);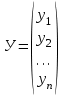 – объем продукции конечного потребления (вектор конечного потребления) – объем продукции конечного потребления (вектор конечного потребления)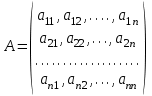 – матрица коэффициентов прямых затрат. – матрица коэффициентов прямых затрат.Система уравнений 4.3 в матричной форме имеет вид 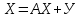 (3.4 (3.4Определение. Соотношение 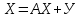 называется уравнением линейного межотраслевого баланса (или модели Леонтьева). называется уравнением линейного межотраслевого баланса (или модели Леонтьева).3.2. Основная задача межотраслевого баланса Уравнение межотраслевого баланса используется для решения следующих целей: – требуется рассчитать вектор конечного потребления У,  если известен вектор валового выпуска Х; если известен вектор валового выпуска Х;– требуется определить вектор Х валового выпуска продукции для периода Т (например, год), если известен вектор конечного потребления У. Решая систему линейных уравнений 3.4 при известных начальных условиях и условии не отрицательности элементов матрицы А и векторов Х и У отыскивается согласно задачам отраслевого баланса неизвестный вектор. Продуктивные модели Леонтьева Определение. Матрица А (и модель Леонтьева), все элементы которой неотрицательны, называется продуктивной, если для любого вектора У с неотрицательными компонентами существует решение уравнения 3.4 — вектор Х, все элементы которого неотрицательны. Теорема 3.1. Если для матрицы А с неотрицательными элементами и некоторого вектора У с неотрицательными компонентами уравнение имеет решение Х с неотрицательными компонентами, то матрица А продуктивна. Достаточно установить наличие хотя бы для одного решения –положительного вектора У системы уравнений 1.4.4, чтобы матрица А была продуктивной. Перепишем систему 3.4 с использованием единичной матрицы Е в виде 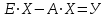 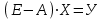 (3.5) (3.5)Если существует обратная матрица 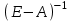 , то существует и единственное решение уравнения 3.5 , то существует и единственное решение уравнения 3.5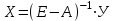 . (3.6) . (3.6)Определение. Матрица 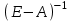 называется матрицей полных затрат. называется матрицей полных затрат.Критерии продуктивности матрицы А Первый критерий продуктивности. Матрица А продуктивна тогда и только тогда, когда матрица 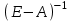 существует и ее элементы неотрицательны. существует и ее элементы неотрицательны.Второй критерий продуктивности. Матрица А с неотрицательными элементами продуктивна, если сумма элементов по любому ее столбцу (строке) не превосходит единицы, причем хотя бы для одного столбца (строки) эта сумма строго меньше единицы: 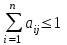 . (3.7) . (3.7)Пример 1. На основании информации представленной в таблице 1 по балансу за некоторый период между пятью видами экономической деятельности. Таблица 1.
Определить: 1. Вектор конечного потребления. 2. Вектор валового выпуска. 3. Матрицу коэффициентов прямых затрат и оценить ее продуктивность. Решение. Условие задачи приведено в соответствии с соотношениями 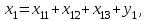 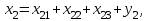 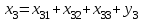 . .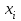 . — общий объем (валовой выпуск) продукции i-го вида экономической деятельности; . — общий объем (валовой выпуск) продукции i-го вида экономической деятельности;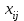 . — объем продукции i-го вида экономической деятельности (производителя), потребляемый j-м потребителем для производства объема продукции . — объем продукции i-го вида экономической деятельности (производителя), потребляемый j-м потребителем для производства объема продукции 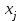 ; ;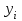 — объем продукции i-го производителя , предназначенный для реализации (потребления) в непроизводственной сфере (продукт конечного потребления). — объем продукции i-го производителя , предназначенный для реализации (потребления) в непроизводственной сфере (продукт конечного потребления). (i, j = 1, 2, 3, 4, 5). Согласно формуле 1.4.2 перепишем условие в виде векторов и матрицы А: 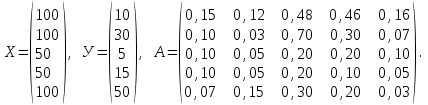 Все элементы матрицы А положительны, однако нетрудно видеть, что их сумма в третьем и четвертом столбцах больше единицы. Следовательно, условия второго критерия продуктивности не соблюдены, и матрица А не является продуктивной. Экономическая причина этой непродуктивности заключается в том, что внутреннее потребление видов экономической деятельности велико в соотношении с их валовым выпуском. Контрольные вопросы к разделу 1 1. Чему равен определитель 3-го порядка, в котором имеются две пропорциональные строки? 2. Чем отличается минор данного элемента определителя от его алгебраического дополнения? 3. Как вычисляется определитель n-го порядка? 4. На чем основан метод накопления нулей для вычисления определителя? 5. Какие существуют методы решения произвольного числа линейных уравнений с произвольным числом неизвестных? 6. Какие переменные называются базисными и какие – свободными? 7. Дайте экономическую интерпретацию коэффициентов прямых и полных затрат? 8. В каком виде представляется соотношение баланса, если условие сбалансированной торговли для одной из стран не выполняется? Тестовые задания для самопроверки к разделу 1 1.Определитель не равный нулю может иметь вид… Варианты ответов: 1.  2. 2. 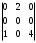 3. 3.  4. 4.  2. Даны матрицы 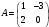 и и 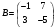 Тогда матрица С = 2А + В имеет вид … Тогда матрица С = 2А + В имеет вид …Варианты ответов: 1). 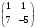 2). 2).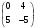 3). 3).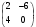 4). 4).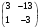 3. Дана матрица 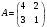 Тогда матрица C=A2 имеет вид … Варианты ответов: 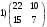 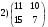 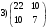 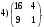 4. Для невырожденной матрицы A решение системы AX=B в матричной форме имеет вид… Варианты ответов: 1. X=A∙B-1 2. X= A-1∙B 3. X=B1∙ A-1 4. X= B-1∙ A 5. Дана матрица 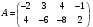 Тогда ранг матрицы А равен … Тогда ранг матрицы А равен …Варианты ответов: 1). 0. 2). 4. 3). 1. 4). 2 6. Для матрицы A существует обратная, если она равна … Варианты ответов: 1). 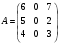 2). 2). 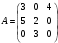 3). 3). 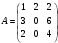 4). 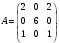 7. Система линейных уравнений 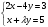 не имеет решений, если λ равно …. не имеет решений, если λ равно ….Варианты ответов: 1).-2. 2).8. 3).-8. 4). 2. 8. Если структурная матрица торговли трех стран имеет вид 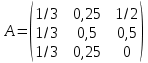 то соотношение национальных доходов стран для сбалансированной торговли равно: то соотношение национальных доходов стран для сбалансированной торговли равно:1) 3:4:2 2) 2:4:1 3)3:2:2 4) 3:4:5 9. Известно, что суммарный доход трех стран равен 402 усл. ден. ед. и структурная матрица торговли А., то равновесный вектор национальных доходов равен: 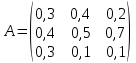 1) (134, 201, 67) 2) (135, 207, 69) 3) (133, 211, 67) 4) (135, 201, 66) Раздел 2. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Глава 4. Общая задача линейного программирования. Методы решения задач линейного программирования: графические и аналитические 4.1. Общая задача линейного программирования Линейное программирование (ЛП) изучает задачи нахождения экстремума линейной функции нескольких переменных при линейных ограничениях на переменные. При этом множество значений переменных, удовлетворяющих линейным ограничениям задачи, называется допустимым множеством. Линейная функция, экстремум которой ищется, называется целевой функцией. Линейное программирование сформировалось как отдельный раздел прикладной математики в 40 − 50-х годах XX века благодаря работам советского математика Л. В. Канторовича. В 1975 году Л. В. Канторович был удостоен Нобелевской премии по экономике «за вклад в теорию оптимального распределения ресурсов». В общем виде задача линейного программирования формулируется следующим образом: максимизировать (минимизировать) целевую функцию 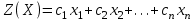 , (4.1) , (4.1)при ограничениях: 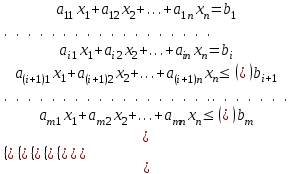 (4.2) (4.2)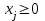 , ,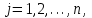 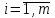 , , 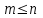 , (4.3) , (4.3)где 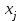 − неизвестные; aij , bi , сj – заданные постоянные величины. − неизвестные; aij , bi , сj – заданные постоянные величины.Приведем математическую модель задачи наилучшего распределения ресурсов ([1] − [4]). Пусть предприятие из m видовресурсов производит n видов продукции. Предположим, что для производства одной единицы 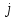 -го вида продукции расходуется aijединиц i-го вида ресурса. Запасы каждого ресурса и прибыль, получаемая от реализации одной единицы каждого вида продукции, заданы. Нужно составить план производства изделий, обеспечивающий максимальную суммарную прибыль от реализации продукции. Составить математическую модель этой задачи. -го вида продукции расходуется aijединиц i-го вида ресурса. Запасы каждого ресурса и прибыль, получаемая от реализации одной единицы каждого вида продукции, заданы. Нужно составить план производства изделий, обеспечивающий максимальную суммарную прибыль от реализации продукции. Составить математическую модель этой задачи. Введем переменные 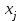 ( (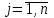 ) − количество каждого вида продукции, которое необходимо произвести; bi – запас ресурса i-го типа, ) − количество каждого вида продукции, которое необходимо произвести; bi – запас ресурса i-го типа, 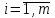 ; сj – прибыль от реализации одной единицы ; сj – прибыль от реализации одной единицы 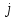 -го вида продукции -го вида продукции 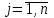 . .Линейная математическая модель поставленной задачи имеет вид: 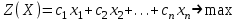 , ,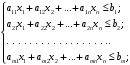 (4.4) (4.4)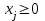 , , 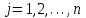 . .Приведем пример экономической задачи, сводящейся к линейной модели. Пример 1. Для производства изделий двух видов используется четыре типа технологического оборудования. Временные затраты на производство изделий и временной ресурс оборудования представлены в таблице 4.1. Доход от реализации готового изделия 1-го вида составляет 50 тысяч рублей, а изделия 2-го вида – 20 тысяч. Найти оптимальный план производства изделий 1-го и 2-го вида, обеспечивающих максимальную прибыль от их реализации. Таблица 4.1
Требуется составить математическую модель этой задачи. Решение: Для решения данной задачи необходимо составить ее математическую модель. Введем переменные: x1 – число изделий первого вида; x2 – число изделий второго вида. Составим целевую функцию: Z – прибыль от реализации изделий: Z= 50 x1 + 20 x2® max. (4.5) Система ограничений имеет вид: 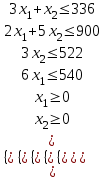 . (4.6) . (4.6)Данная модель является линейной. После сокращения система ограничений имеет вид: 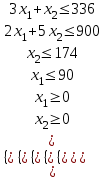 4.1. Графический метод решения задач линейного программирования Если число переменных в задаче ЛП равно двум, а ограничениями является система неравенств, то задачу можно решать графическим методом. Приведем алгоритм решения задачи ЛП графическим методом: Строится область допустимых решений. Если это множество равно нулю, то задача не имеет решения. Строим вектор 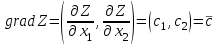 . .Перпендикулярно к вектору 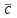 проводится одна из линий уровня: проводится одна из линий уровня: 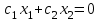 . .Линия уровня перемещается до положения опорной прямой. Опорной прямой называют линию уровня, имеющую общие точки с областью допустимых решений (О.Д.Р.) и расположенную так, что О.Д.Р. целиком находится в одной из полуплоскостей. Если точка А – последняя точка встречи прямой уровня с О.Д.Р., то Z(A) является максимальным значением целевой функции в О.Д.Р. Если окажется, что линия уровня параллельна одной из сторон О.Д.Р., то экстремум достигается во всех точках соответствующей стороны. Рассмотрим графическое решение задачи, сформулированной в примере 1. С этой целью построим в плоскости х1Ох2 О.Д.Р. Каждое неравенство системы ограничений определяет в плоскости х1Ох2 полуплоскость, лежащую ниже (выше) прямой, определяемой соответствующим уравнением. Построим прямые: 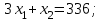 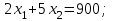 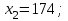 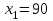 ; ; 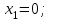 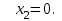 Возьмем точку О с координатами Возьмем точку О с координатами 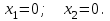 Поставив их в первые четыре неравенства, получаем верные неравенства. Следовательно, искомые полуплоскости лежат ниже соответствующих прямых. Поставив их в первые четыре неравенства, получаем верные неравенства. Следовательно, искомые полуплоскости лежат ниже соответствующих прямых.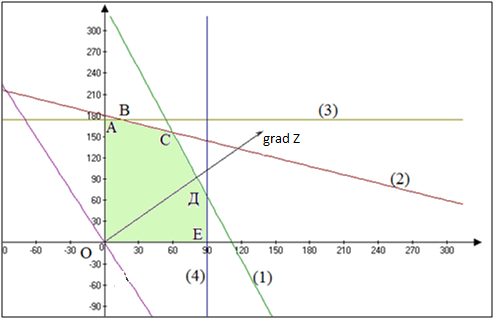 Рис. 4.1. Область допустимых решений Область ОАВСДЕ (рис. 4.1) - О.Д.Р. Строим на рисунке 4.1 вектор 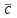 , его направление показывает направление возрастания целевой функции Z, в противоположном направлении функция убывает. Определяем граничную точку О.Д.Р., в которой функция Z принимает максимальное значение. В нашем случае – это точка С. Вычислим координаты точки С, решая систему из уравнений прямых (1) и (2), на пересечении которых находится точка С. Получаем С(60,156). Это и будет оптимальное решение данной задачи, которому соответствует максимальное значение целевой функции , его направление показывает направление возрастания целевой функции Z, в противоположном направлении функция убывает. Определяем граничную точку О.Д.Р., в которой функция Z принимает максимальное значение. В нашем случае – это точка С. Вычислим координаты точки С, решая систему из уравнений прямых (1) и (2), на пересечении которых находится точка С. Получаем С(60,156). Это и будет оптимальное решение данной задачи, которому соответствует максимальное значение целевой функции 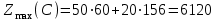 тыс. руб. тыс. руб.4.3. Переход от общей задачи ЛП к канонической форме Математическая модель задачи ЛП может быть канонической и неканонической (стандартной). В случае, когда все ограничения (4.2) в задаче ЛП являются уравнениями и все переменные неотрицательные, задачу линейного программирования называют канонической. В стандартной форме линейная математическая модель задачи ЛП имеет вид (4.1) – (4.3). Метод ее решения – симплексный метод. Для n переменных О.Д.Р. – выпуклый n-мерный многогранник [3] с конечным числом угловых точек, которые алгебраически представляют некоторые опорные решения системы ограничений. Справедлива теорема об экстремуме целевой функции. Теорема 4.1. Если область допустимых решений (О.Д.Р.) замкнутая и ограниченная, то оптимальное решение задачи ЛП существует, причем, хотя бы одно из опорных решений системы ограничений является оптимальным решением этой задачи. Симплекс-метод является универсальным и предназначен для решения задачи ЛП в канонической форме. Общий вид канонической задачи ЛП может быть представлен в координатной, векторной или матричной форме записи: а) каноническая задача ЛП в координатной форме имеет вид:  ; (4.7) ; (4.7)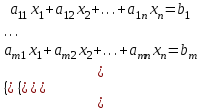 ( 4.8) ( 4.8)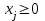 , , 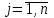 . .б) каноническая задача ЛП в векторной форме имеет вид: 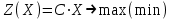 , ,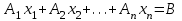 , (4.9 ) , (4.9 )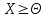 , ,где 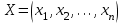 ; ; 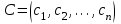 ; ; 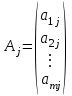 , , 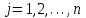 ; ; 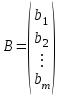 ; ; 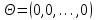 . .в) каноническая задача ЛП в матричной форме имеет вид: 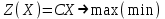 , ,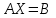 , , 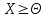 , ,где 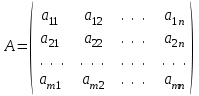 , , 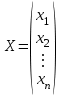 , , 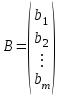 . .При составлении математических моделей экономических задач ограничения в основном формируются в системы неравенств. Поэтому необходимо переходить от неравенств к системам уравнений. Например, рассмотрим линейное неравенство 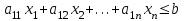 (4.10) (4.10)и прибавим к его левой части некоторую величину 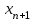 такую, чтобы неравенство превратилось в равенство. такую, чтобы неравенство превратилось в равенство.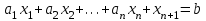 , (4.11) , (4.11)где 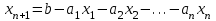 . .Неотрицательная переменная 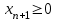 называется дополнительной переменной. Как показано в [3] теорема 1.1 даёт основание для возможности такого преобразования. называется дополнительной переменной. Как показано в [3] теорема 1.1 даёт основание для возможности такого преобразования.Пример 2. Записать в канонической форме задачу (4.5) – (4.6). Решение: Приведем задачу к каноническому виду, введя с этой целью новые переменные: 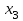 , ,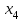 , , 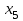 , ,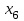 . .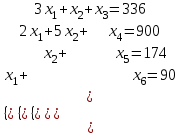 (4.12) (4.12)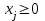 , , 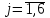 . .Z= 50 x1 + 20 x2+0 x3 +0 x4 +0 x5 +0 x6 ®max. 4.4. Симплексный метод решения задач линейного программирования Симплексный метод состоит в целенаправленном переборе опорных решений задачи ЛП. Он позволяет за конечное число шагов либо найти оптимальное решение, либо установить, что его не существует. Содержание метода: 1. Найти начальное опорное решение. 2. Указать способ перехода от одного опорного решения к другому, на котором значение целевой функции ближе к оптимальному. 3. Задать критерии, которые позволяют своевременно прекратить проверку решений на оптимальность или сделать заключение об отсутствии оптимального решения. Опорным решением задачи ЛП называется такое допустимое решение 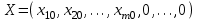 , для которого векторы условий (столбцы коэффициентов при неизвестных в системе ограничений) А1, А2, …, Аm, соответствующие положительным координатам, линейно независимы. Будем считать, что система ограничений состоит из линейно независимых уравнений. Число отличных от нуля координат опорного решения равно m. , для которого векторы условий (столбцы коэффициентов при неизвестных в системе ограничений) А1, А2, …, Аm, соответствующие положительным координатам, линейно независимы. Будем считать, что система ограничений состоит из линейно независимых уравнений. Число отличных от нуля координат опорного решения равно m. Базисом опорного решения называется базис системы векторов условий задачи, включающий в свой состав векторы, соответствующие отличным от нуля координатам опорного решения. Базисное решение находится методом Жордана-Гаусса. При этом разрешающие элементы для преобразований Жордана необходимо выбирать из условия, обеспечивающего неотрицательность правых частей уравнений системы, 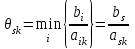 при при 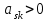 . (4.13) . (4.13) Здесь k – номер вектора условия Ak, вводимого в базис (номер выбираемого столбца матрицы системы ограничений), а s– номер вектора As, выводимого из базиса (номер строки матрицы системы, в которой следует выбирать разрешающий элемент для преобразования Жордана). С помощью данного условия можно выбрать разрешающий элемент в любом столбце k матрицы системы ограничений, в котором имеется хотя бы один положительный элемент. Если при выборе разрешающего элемента данное условие нарушается, в правой части системы уравнений появляются отрицательные величины. Приведем общую схему симплекс-метода для решения задачи (4.7) – (4.8) на max: 1) Пусть дан базис некоторого опорного решения и соответствующая ему симплекс-таблица. В верхней строке этой таблицы (см. пример 3, заголовки столбцов) располагаются свободные переменные, в крайнем левом столбце – базисные переменные; крайний правый столбец – это столбец свободных членов, а самая нижняя строка является строкой целевой функции и называется вектором относительных оценок. Остальное содержимое таблицы - столбцы матрицы ограничений, отвечающие соответствующим столбцам свободных переменных. Координаты вектора относительных оценок (1, 2,… n) находят по правилу: для нахождения коэффициента k вектор из коэффициентов при базисных переменных в целевой функции скалярно умножить наk-й столбец симплекс-таблицы и вычесть из найденного числа коэффициент целевой функции при соответствующем свободном переменном xk. 2) Если все относительные оценки (нижняя строка этой таблицы) неотрицательны, то построено оптимальное опорное решение. 3) Если существует отрицательная оценка и соответствующий ей столбец (разрешающий) состоит из неположительных элементов, то имеет место неразрешимость целевой функции Z(X), то есть max Z(X) +. 4) Иначе, выбрать ведущий элемент (задаёт ведущую строку) и сделать с ним шаг жордановых исключений, перейдя к новой симплекс-таблице, которую проанализировать как в пункте 2. Пример 3. Решить симплекс-методом задачу (4.12) из примера 2. Решение: Объявляем х1, х2 свободными переменными; х3, х4, х5, х6 – базисными переменными, так как соответствующие им векторы A3, A4 ,A5, A6 линейно независимы. Составим симплекс-таблицу, соответствующую первоначальному опорному плану
Составим начальный опорный план: 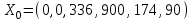 , , 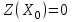 В последней строке имеются две отрицательные оценки. Следовательно, Х0 не является оптимальным решением и его надо улучшить. В качестве ведущего столбца возьмем столбец переменной х1, а за ведущую строку – строку переменной х6, так как В последней строке имеются две отрицательные оценки. Следовательно, Х0 не является оптимальным решением и его надо улучшить. В качестве ведущего столбца возьмем столбец переменной х1, а за ведущую строку – строку переменной х6, так как 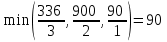 . Ведущий элемент равен 1. . Ведущий элемент равен 1. Запишем правила перехода к новой симплекс-таблице: 1. Базисная переменная, находящаяся в ведущей строке, и свободная переменная, находящаяся в ведущем столбце, меняются местами. 2. Ведущий элемент заменяется величиной, ему обратной. 3. Все элементы ведущей строки (включая свободный член), кроме ведущего элемента, заменяются их отношениями к ведущему элементу. 4. Все элементы ведущего столбца (кроме ведущего элемента) заменяются взятыми с обратными знаками их отношениями к ведущему элементу. 5. Остальные элементы заменяются по «правилу 4 элементов»: любой такой элемент умножается на ведущий и из произведения вычитается произведение двух других элементов, составляющих с первыми вершины прямоугольника, после чего результат делится на ведущий элемент. Составляем новую симплекс-таблицу по этим правилам:
В последней строке имеем отрицательную оценку. Находим 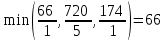 . Ведущий элемент равен 1. Составим опорный план: . Ведущий элемент равен 1. Составим опорный план: 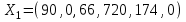 , , 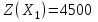 . .Переходим к новой симплекс-таблице.
В последней строке имеем отрицательную оценку. Надо улучшать план. Вычислим 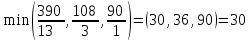 . Ведущий элемент равен 13. Составим опорный план: . Ведущий элемент равен 13. Составим опорный план: 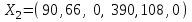 , , 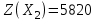 . .Полученный опорный план не является оптимальным. Новая симплекс-таблица.
Получаем: 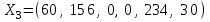 , , 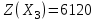 . .Полученный план является оптимальным. Ответ: 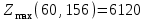 . . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||