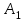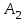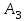Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
Полученное решение Х0 имеет m+n-1=6 базисных переменных. Вычислим значение целевой функции Z(Х0)=150. 3. Для проверки оптимальности опорного решения необходимо найти потенциалы. С этой целью используем формулы (5.6), (5.9), (5.10). .Записываем систему уравнений для нахождения потенциалов и решаем ее. 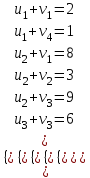 (5.11 ) (5.11 )Система состоит из шести уравнений и имеет 7 неизвестных. Система неопределенна. Следовательно, одному из потенциалов задаем произвольно значение, пусть u2=0. Тогда v1=8, v2=3, v3=9. Остальные потенциалы находим из системы (5.11 ): u1=-6, u3=-3, v4=7. Значения потенциалов записываем в таблицу 5.11. Таблица 5.11
4. Проверяем опорное решение X0 на оптимальность. С этой целью в каждой незаполненной клетке вычисляем оценки 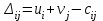 . . Положительные оценки имеем в клетках А2В4, А3В4. В этих клетках Δ24=5, Δ34=1. Выбираем клетку с наибольшей разностью. Для клетки А2В4 строим цикл. Ставим в эту клетку знак «+», присоединяем ее к занятым клеткам. Строим цикл(см табл.). В угловых точках цикла расставляем поочередно знаки «+» и «-», начиная с «+» в клетке А2В4. В клетки, отмеченные знаком «+», добавляется груз λ, а из клеток, отмеченных знаком «-»,убавляется такой же по величине груз. Определяем величину груза λ, перераспределяемого по циклу. Она равна значению наименьшей из перевозок в клетках цикла, отмеченных знаком «-»: 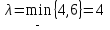 . Осуществляем сдвиг по циклу на величину λ =4 (таблица 5.12-5.13). . Осуществляем сдвиг по циклу на величину λ =4 (таблица 5.12-5.13).Таблица 5.12
Осуществляем сдвиг по циклу на величину θ=4. Получаем второе опорное решение Х2. Таблица 5.13
Проверим опорное решение X2 на оптимальность. Все оценки неположительны. Следовательно, решение является оптимальным. Zmin(X2)=120 при 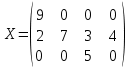 . .5.6. Решение транспортной задачи с помощью надстройки «Поиск решения» в среде Excel. Итак, рассмотрим пример. 3 ТЗ, для решения которой используется надстройки «Поиск решения» в среде Excel. Пример 4. Задано четыре поставщика некоторого продукта и четыре потребителя с соответствующими параметрами aiи bj (см. таблицу в примере 3) и заданы соответствующие значения cijматрицы стоимостей перевозок единицы продукта. Все эти значения можно увидеть на рис. 5.7. В интервале B2:E2 помещены значения b1, b2, b3 , b4 (потребности), а в интервале A3:A5 помещены значения a1, a2 , a3 (предложения поставщиков). Так как суммы значений из первой строки и из первого столбца равны, ясно, что задача закрытая. Интервал H3:K5 содержит значения стоимостей перевозки 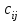 . .1. Вставьте новый лист в свою рабочую книгу и занесите данные так, как это показано на рис. 5.7. 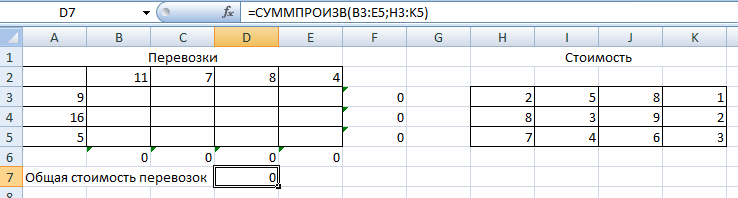 Рис. 5.7. Введены исходные данные В ячейку F3 поместите формулу для суммы элементов строки (B3:E3) и заполните ряд вниз с помощью маркера автозаполнения. Формулу суммирования элементов интервала (B3:B5) введите в ячейку В6 и заполните ряд вправо. Так как суммируемые ячейки еще ничего не содержат, результатом суммирования оказываются нулевые значения. Целевая функция, выражающая общую стоимость перевозок, есть сумма соответствующих произведений количества перевозимого продукта на стоимость доставки единицы продукта. Введите в ячейку D7 формулу =СУММПРОИЗВ(B3:E5;H3:K5) (рис. 5.8). 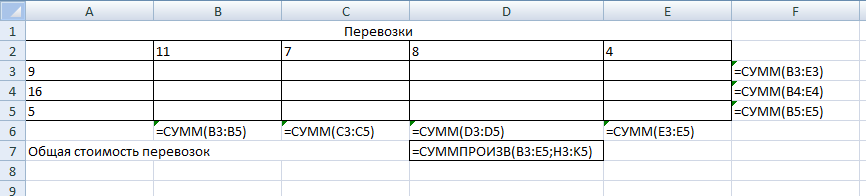 Рис. 5.8. Введены зависимости для целевой функции и всех ограничений 2. Выполните команду Поиск решения. В появившемся диалоговом окне заполним поля согласно рис. 5.9. 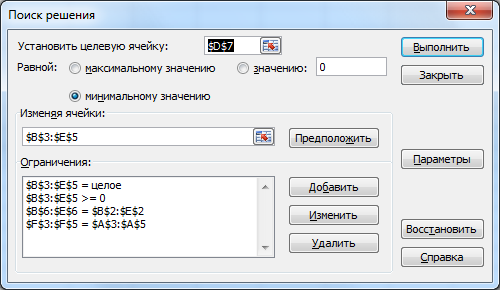 Рис. 5.9.Введены все условия задачи 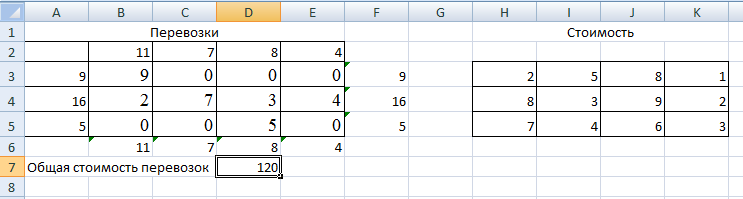 Рис. 5.10. Решение получено Обратите внимание, что перевозки не могут быть отрицательными. Такое ограничение необходимо добавлять при решении задачи. Также заметим, что при вводе ограничений допустимо оперировать с интервалами, а не только с отдельными ячейками. Ограничение о целочисленности решения, возможно, не обязательно, но требование его выполнения естественно. Если все сделано правильно, Excel сообщит о том, что решение найдено и удовлетворяет ограничениям. В целевой ячейке теперь результатом формулы является значение 120. В интервал B3:E5 занесены значения перевозок от поставщиков к потребителям. Контрольные вопросы к разделу 2 1. Сформулируйте общую задачу линейного программирования. Запишите каноническую задачу линейного программирования. 2. С помощью каких преобразований осуществляется переход от одной формы записи задачи к другой? 3. Запишите математические модели основных типовых задач линейного программирования. Сформулируйте алгоритм графического метода решения ЗЛП. 4. Какая форма записи ЗЛП используется для решения симплекс-методом? Какая форма записи ЗЛП используется для решения графическим методом? 5. В чем суть метода искусственного базиса? 6. Опишите алгоритм решения задачи ЛП в Excel. 7. Дайте определение двойственной задачи. Перечислите правила построения двойственной задачи. В какой форме должна быть записана исходная задача линейного программирования, чтобы по ней легко было составить двойственную задачу? 8. Сформулируйте теоремы двойственности. 5. Как связаны оптимальные значения целевых функций взаимно-сопряженных двойственных задач? 6. Дайте определение транспортной задачи: открытой и закрытой. Назовите условие разрешимости транспортной задачи. 7. В чем суть метода северо-западного угла при составлении опорного плана? 8. В чем суть метода минимального элемента? В чем суть метода Фогеля? 9. Какой критерий оптимальности используется при решении транспортной задачи? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||