Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
Функция распределения будет иметь вид: при 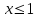 получаем получаем 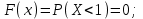 при при 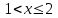 получаем получаем 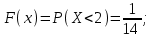 при при 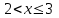 получаем получаем 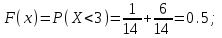 при при 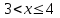 получаем получаем 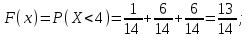 при при 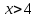 получаем получаем 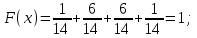 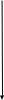 F(x) F(x) 1 113/14   1/2 1/2 1/14 1/14 0 1 2 3 4 х 0 1 2 3 4 хРисунок 8.3. Функция распределения дискретной случайной величины имеет 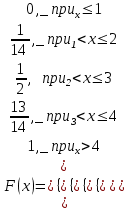 Для характеристики непрерывной случайной величины применяется функция распределения вероятностей, которая, так же как и для дискретной случайной величины, представляет собой вероятность события X< х: F(x) = P(X<x). Необходимо учитывать, что в отличие от дискретной случайной величины непрерывная случайная величина Х принимает все возможные значения из некоторого промежутка, функция F(x) является монотонно возрастающей. График такой функции часто имеет вид, представленный на рис. 8.4. Здесь предполагается, что х меняется от 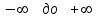 . .F(x) 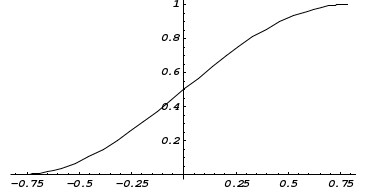 х хРисунок 8.4. Функция распределения непрерывной случайной величины. В некоторых случаях на значения случайной величины могут быть наложены ограничения. В этом случае график функции распределения имеет свои особенности. Свойства функции распределения 1) Если F(x) – функция распределения случайной величины Х, то значения функции распределения принадлежат отрезку [0, 1]. 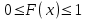 2) Функция распределения случайной величины F(x) – неубывающая функция.  при при 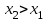 3) Вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна нулю. 4) Если F(x) – функция распределения случайной величины Х, то 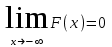 , , 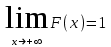 5) Вероятность того, что случайная величина примет значение, заключенное в интервале (a, b) , равна приращению функции распределения на этом интервале. 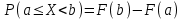 . .Для непрерывной случайной величины согласно свойству (3) это неравенство перепишем в виде 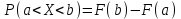 . .Определение. Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x). 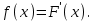 (8.2) (8.2)Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема. Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов. После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины. Определение. Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением (может быть, конечного числа точек). Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина Х примет значение, принадлежащее заданному интервалу. Теорема 8.1. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу (a, b), равна определенному интегралу от плотности распределения, взятому в пределах от a до b. 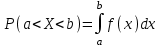 (8.3) (8.3)Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения, записанном выше. Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (a, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми x=aи x=b. Функция распределения может быть легко найдена, если известна плотность распределения, по формуле: 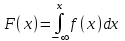 (8.4) (8.4)Свойства плотности распределения 1) Плотность распределения – неотрицательная функция. 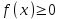 2) Несобственный интеграл от плотности распределения в пределах от - до равен единице. 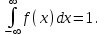 Пример 3. Задана непрерывная случайная величина х своей функцией распределения f(x). 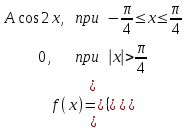 Определить коэффициент А, найти функцию распределения, построить графики функции распределения и плотности распределения, определить вероятность того, что случайная величина х попадет в интервал  . .Найдем коэффициент А. 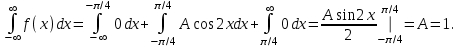 Найдем функцию распределения: 1) На участке 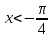 : :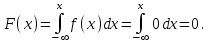 2) На участке   3) На участке 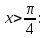 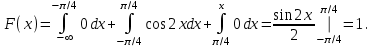 Итого: 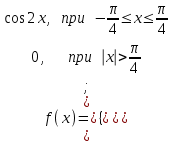  Построим график плотности распределения: f(x) 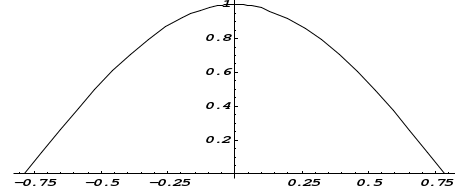 Построим график функции распределения: F(x)  х хНайдем вероятность попадания случайной величины в интервал  . . Ту же самую вероятность можно искать и другим способом:  8.3.Числовые характеристики случайной величины При решении ряда практических задач не всегда возможно найти закон распределения случайной величины, можно ограничиться нахождением числовых значений, которые описывают случайную величину суммарно. Эти числа называют числовыми характеристиками случайной величины. К числу таких характеристик относят математическое ожидание, дисперсия. среднее квадратическое отклонение, мода, медиана, коэффициент асимметрии, эксцесс, коэффициент вариации. Определение. Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности. 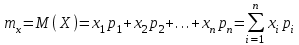 (8.5) (8.5)С точки зрения вероятности можно сказать, что математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины. Пример 4. Закон распределения случайной величины имеет вид:
|
