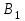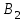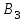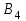Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
5.4. Переход от одного опорного решения к другому. В транспортной задаче переход от одного опорного решения к другому осуществляется с помощью цикла. Для некоторой свободной клетки таблицы строится цикл, содержащий часть клеток, занятых опорным решением. По этому циклу перераспределяются объемы перевозок (осуществляется сдвиг по циклу). Перевозка «загружается» в выбранную свободную клетку и освобождается одна из занятых клеток, получается новое опорное решение. Если таблица транспортной задачи содержит опорное решение, то для любой свободной клетки таблицы существует единственный цикл, содержащий эту клетку и часть клеток, занятых опорным решением. Для удобства вычислений вершины циклов нумеруют и отмечают нечетные знаком «+», а четные знаком «-». Такой цикл называется означенным (рис. 5.6). 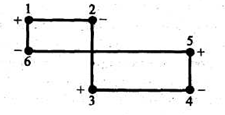 Рис 5.6.Означенный цикл. Сдвигом по циклу на величину λ называется увеличение объемов перевозок во всех нечетных клетках цикла, отмеченных знаком «+», и уменьшение объемов перевозок на ту же величину λ во всех четных клетках, отмеченных знаком «-». 5.5. Метод потенциалов Широко распространенным методом решения транспортных задач является метод потенциалов. Если допустимое решение 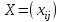 , , 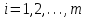 ; ; 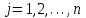 транспортной задачи является оптимальным, то существуют потенциалы (числа) поставщиков транспортной задачи является оптимальным, то существуют потенциалы (числа) поставщиков 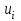 , , 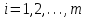 и потребителей и потребителей 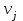 , , 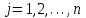 удовлетворяющие следующим условиям: удовлетворяющие следующим условиям: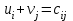 при xij > 0, (5.6) при xij > 0, (5.6)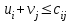 при xij = 0. (5.7) при xij = 0. (5.7)Группа равенств (5.6) используется как система уравнений для нахождения потенциалов. Данная система уравнений имеет m+n неизвестных 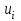 , , 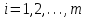 и потребителей и потребителей 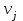 , , 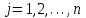 , . Число уравнений системы, как и число отличных от нуля координат невырожденного опорного решения, равно m+n-1. Так как число неизвестных системы на единицу больше числа уравнений, то одной из них можно задать значение произвольно, а остальные найти из системы (5.6). Группа неравенств (5.7) используется для проверки оптимальности опорного решения. Эти неравенства удобнее представить в следующем виде: , . Число уравнений системы, как и число отличных от нуля координат невырожденного опорного решения, равно m+n-1. Так как число неизвестных системы на единицу больше числа уравнений, то одной из них можно задать значение произвольно, а остальные найти из системы (5.6). Группа неравенств (5.7) используется для проверки оптимальности опорного решения. Эти неравенства удобнее представить в следующем виде: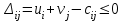 при xij = 0. (5.8) при xij = 0. (5.8)Числа 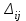 называются оценками для свободных клеток таблицы (векторов условий) транспортной задачи. Опорное решение является оптимальным, если для всех векторов условий (клеток таблицы) оценки неположительные. Оценки для свободных клеток транспортной таблицы используются при улучшении опорного решения. для этого находят клетку (l,k) таблицы, соответствующую называются оценками для свободных клеток таблицы (векторов условий) транспортной задачи. Опорное решение является оптимальным, если для всех векторов условий (клеток таблицы) оценки неположительные. Оценки для свободных клеток транспортной таблицы используются при улучшении опорного решения. для этого находят клетку (l,k) таблицы, соответствующую 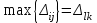 . Если . Если 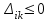 , то решение оптимальное. Если же , то решение оптимальное. Если же  , то для соответствующей клетки (l,k) строят цикл и улучшают решение, перераспределяя груз , то для соответствующей клетки (l,k) строят цикл и улучшают решение, перераспределяя груз 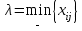 по этому циклу. по этому циклу.Алгоритм решения транспортных задач методом потенциалов: 1. Проверить выполнение необходимого и достаточного условия разрешимости задачи. Если задача имеет неправильный баланс, то вводится фиктивный поставщик или потребитель с недостающими запасами или запросами и нулевыми стоимостями перевозок. 2. Построить начальное опорное решение (методом минимальной стоимости или каким-либо другим методом). проверить правильность его построения по количеству занятых клеток (их должно быть m+n-1) и убедиться в линейной независимости векторов условий (используя метод вычеркивания). 3. Построить систему потенциалов, соответствующих опорному решению. Для этого решают систему уравнений 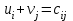 при xij > 0, при xij > 0,которая имеет бесконечное множество решений. Для нахождения частного решения системы одному из потенциалов (обычно тому. которому соответствует большее число занятых клеток) задают произвольно некоторое значение (чаще ноль). Остальные потенциалы однозначно определяются по формулам 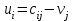 при xij > 0, (5.9) при xij > 0, (5.9)если известен потенциал 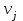 , и , и 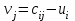 при xij > 0, (5.10) при xij > 0, (5.10)если известен потенциал 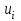 . .4. Проверить выполнение условия оптимальности для свободных клеток таблицы. Для этого вычисляют оценки для всех свободных клеток по формулам 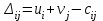 и те из них, которые больше нуля, записывают в левые нижние углы клеток. Если для всех свободных клеток 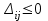 , то вычисляют значение целевой функции и решение задачи заканчивается, так как полученное решение является оптимальным. Если же имеется хотя бы одна клетка с положительной оценкой, опорное решение не является оптимальным. , то вычисляют значение целевой функции и решение задачи заканчивается, так как полученное решение является оптимальным. Если же имеется хотя бы одна клетка с положительной оценкой, опорное решение не является оптимальным.5. Перейти к новому опорному решению, на котором значение целевой функции будет меньше. Для этого находят клетку таблицы задачи, которой соответствует наибольшая положительная оценка 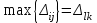 . .Строят цикл, включающий в свой состав данную клетку и часть клеток, занятых опорным решением. В клетках цикла расставляют поочередно знаки «+» и «-», начиная с «+» в клетке с наибольшей положительной оценкой. Осуществляют сдвиг (перераспределение груза) по циклу на величину 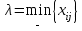 . Клетка со знаком «-», в которой достигается . Клетка со знаком «-», в которой достигается 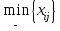 , остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют базисные нули, чтобы число занятых клеток оставалось равным m+n-1. Далее перейти к пункту 3 данного алгоритма. , остается пустой. Если минимум достигается в нескольких клетках, то одна из них остается пустой, а в остальных проставляют базисные нули, чтобы число занятых клеток оставалось равным m+n-1. Далее перейти к пункту 3 данного алгоритма.Пример 3. Решить ТЗ, исходные данные которой заданы в таблице 5.9. Таблица 5.9
Решение: 1. Проверяем необходимое и достаточное условие разрешимости задачи. Находим суммарные запасы поставщиков: 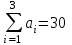 , суммарные запасы потребителей: , суммарные запасы потребителей: 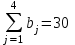 . Имеем задачу с правильным балансом. . Имеем задачу с правильным балансом.2. Находим начальное опорное решение методом минимальной стоимости (таблица 5.10). Таблица 5.10
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||