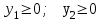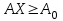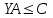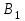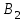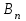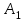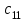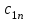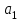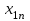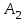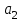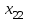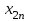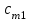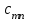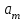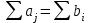Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
5.1. Двойственные задачи линейного программирования. С каждой задачей линейного программирования связана задача, двойственная по отношению к исходной. Обычно из решения одной задачи находят решение другой. Рассмотрим двойственную задачу к задаче использования сырья [3]. Пример 1. Имеются два вида сырья S1 и S2, оставшиеся на предприятии к концу года. Остатки сырья составляют 35 и 20 единиц соответственно. Из этого сырья, с одной стороны, можно наладить производство трех видов товаров Т1, Т2, Т3, и от реализации единицы каждого вида товара получить прибыль 7, 6 и 18 ден. ед. соответственно. Нормы расхода сырья приведены в таблице 5.1. Таблица 5.1
С другой стороны, это сырье можно продать на сторону какой-либо нуждающейся в этом сырье организации. Как следует поступить руководству предприятия? Решение: Количество товаров вида А1, А2 , А3 обозначим через  соответственно. Задачу максимизации прибыли от выпуска товаров можно сформулировать следующим образом: соответственно. Задачу максимизации прибыли от выпуска товаров можно сформулировать следующим образом: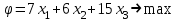 (5.1) (5.1)при условиях  (5.2) (5.2) . .При продаже сырья другой организации возникает вопрос о цене сырья. Обозначим цену единицы сырья S1 через yi, а сырья S2 – через y2. Выручка от продажи сырья должна быть не меньше, чем прибыль от реализации готового изделия. В противном случае лучше изготовить товар и получить от него прибыль. Это требование приведет к неравенствам  . .Для покупателя единственное пожелание состоит в сокращении расходов, т.е. в минимизации функции  . .Таким образом, задачу минимизации расходов от покупки сырья можно сформулировать следующим образом:  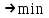 (5.3) (5.3)При ограничениях:  (5.4) (5.4) Найдем решение этой задачи, используя «Поиск решения» в среде Excel: 1. Заполним рабочий лист MS Excel согласно рис.5.1.  Рис. 5.1. Ввод данных задачи (5.3)−(5.4) 2. Выполним команду Поиск решения. В появившемся диалоговом окне заполним поля согласно рис. 5.2. При добавлении ограничений воспользуемся кнопкой Добавить. 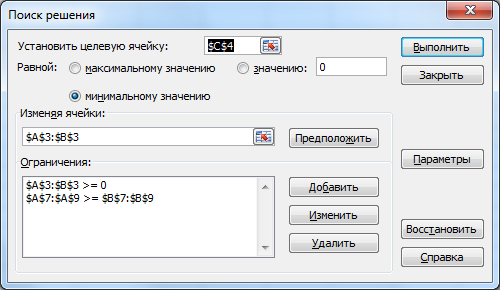 Рис. 5.2. Добавление ограничений 3. После занесения данных нажать на кнопку Выполнить. Получим решение нашей задачи (рис. 5.3)  Рис. 5.3. Полученное решение Затем, используя «Поиск решения» в среде Excel, найдем решение первоначальной задачи (рис.5.4−5.6): 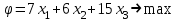 при условиях   . .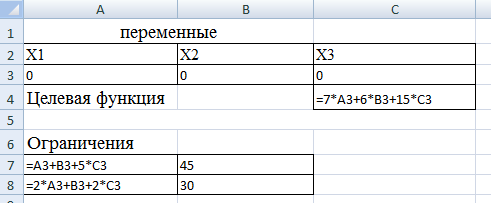 Рис. 5.4. Ввод данных задачи (5.1)−(5.2) 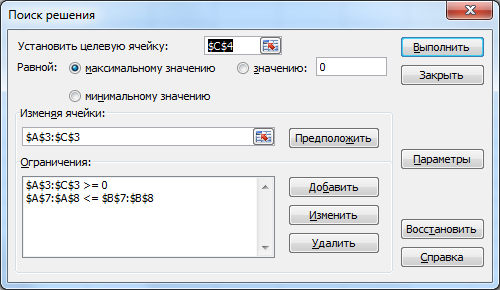 Рис. 5.5. Добавление ограничений В итоге получим  Рис. 5.6. Получено решение задачи (5.1)−(5.2) Эти задачи (5.1) – (5.2) и (5.3) – (5.4) называются двойственными друг другу. Двойственные задачи обладают следующими свойствами ([3], [4]): 1. Коэффициенты  целевой функции исходной задачи являются свободными членами системы ограничений двойственной задачи, свободные члены целевой функции исходной задачи являются свободными членами системы ограничений двойственной задачи, свободные члены 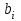 системы ограничений исходной задачи служат коэффициентами целевой функции двойственной задачи. системы ограничений исходной задачи служат коэффициентами целевой функции двойственной задачи.2. Если первая задача имеет размеры 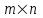 (m ограничений с n неизвестными), то вторая имеет размеры (m ограничений с n неизвестными), то вторая имеет размеры 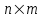 . .3. Матрицы из коэффициентов при неизвестных в левых частях ограничений обеих задач являются взаимно транспонированными. Пусть в первой задаче все неравенства будут типа 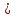 , причем в этой задаче требуется достичь максимума целевой функции , причем в этой задаче требуется достичь максимума целевой функции 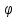 . Во второй задаче неравенства будут типа . Во второй задаче неравенства будут типа 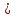 , причем надо достичь минимума целевой функции , причем надо достичь минимума целевой функции  . .Пример двойственных задач, имеющих размеры  и и 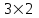 , представлен в табл. 5.2. , представлен в табл. 5.2.Таблица 5.2
Критерий оптимальности. Пусть 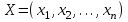 и и 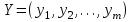 - допустимые решения задач 1 и 2 соответственно. Для того чтобы X было оптимальным решением задачи 1, а Y – оптимальным решением задачи 2, необходимо и достаточно выполнение равенства - допустимые решения задач 1 и 2 соответственно. Для того чтобы X было оптимальным решением задачи 1, а Y – оптимальным решением задачи 2, необходимо и достаточно выполнение равенства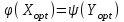 В теории двойственности используются 4 пары двойственных задач:
где С = (c1, c2, …, cn); Y = (y1, y2, …, ym); 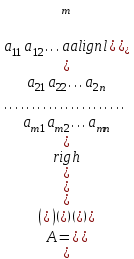 ; ; 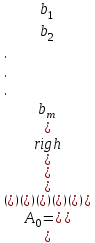 ; ;  . .Теорема 5.1 (1-я теорема двойственности). Если одна из задач взаимно двойственной пары разрешима, то разрешима и другая задача, при этом оптимальные значения целевых функций совпадают. Если целевая функция одной из задач не ограничена (сверху – для задачи максимизации, снизу – для задачи минимизации), то множество допустимых планов другой задачи пусто. Из этой теоремы вытекает следующее Следствие. Для того, чтобы допустимые решения 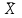 и и  двойственной пары задач были оптимальны, необходимо и достаточно, чтобы значения целевых функций на этих планах совпадали: двойственной пары задач были оптимальны, необходимо и достаточно, чтобы значения целевых функций на этих планах совпадали: . .Теорема 5.2 (2-я теорема двойственности). Пусть имеется симметричная пара двойственных задач 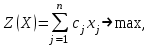   , ,  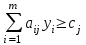 , , 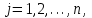 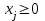 , , 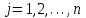 ; ;  , , 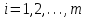 . .Для того чтобы допустимые решения 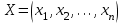 , , 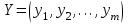 являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства: являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства: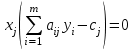 , , 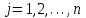 ; ; , , 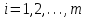 . .Иначе, если при подстановке оптимального решения в систему ограничений i-е ограничение исходной задачи выполняется как строгое неравенство, то i-я координата оптимального решения двойственной задачи равна нулю, и, наоборот, если i-я координата оптимального решения двойственной задачи отлична от нуля, то i-е ограничение исходной задачи удовлетворяется оптимальным решением как равенство . 5.2. Математическая модель транспортной задачи. Условие разрешимости транспортной задачи. Транспортной (ТЗ) называют задачу об оптимальном плане перевозок однородного продукта из пунктов производства (складов) в пункты потребления. Пусть некоторый однородный продукт, сосредоточенный у 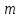 поставщиков поставщиков  в количестве в количестве   единиц соответственно, необходимо доставить единиц соответственно, необходимо доставить 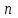 потребителям потребителям  в количестве в количестве 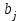  . Известна стоимость . Известна стоимость 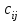 перевозки единицы груза перевозки единицы груза 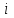 -го поставщика к -го поставщика к 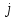 -му потребителю. Необходимо составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребности, и имеющий минимальную стоимость. -му потребителю. Необходимо составить план перевозок, позволяющий вывезти все грузы, полностью удовлетворить потребности, и имеющий минимальную стоимость.Составим математическую модель транспортной задачи. Обозначим через 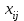 количество единиц груза, запланированного к перевозке от количество единиц груза, запланированного к перевозке от 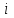 -го поставщика к -го поставщика к 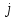 -му потребителю, тогда условие задачи можно записать в виде табл. 5.3, которую также называют матрицей планирования. -му потребителю, тогда условие задачи можно записать в виде табл. 5.3, которую также называют матрицей планирования. Таблица 5.3
Составим математическую модель транспортной задачи (ТЗ). Целевая функция имеет вид 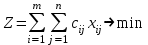 . .Условия удовлетворения спроса:   . .Условия полного вывоза груза: 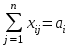  . .Условия неотрицательности:  , , 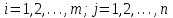 . .Цель - в минимизации полной стоимости перевозок известного количества товаров со складов к потребителю. В рассматриваемой модели предполагается, что суммарные запасы равны суммарным запросам потребителей:  . (5.5) . (5.5) Такая задача называется задачей с правильным балансом, а её модель – закрытой. Если же равенство (5.5) не выполняется, то задача называется задачей с неправильным балансом, а её модель – открытой. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

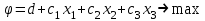 ,
, 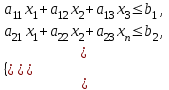
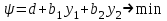 ,
,