Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
Теорема 5.3. Для того чтобы транспортная задача ЛП имела решение, необходимо и достаточно, чтобы суммарные запасы поставщиков равнялись суммарным запросам потребителей, то есть выполнялось условие (5.5). В случае превышения запасов над потребностью вводится фиктивный (n+1)-й потребитель, потребности которого «закрывали» бы ТЗ, а соответствующие тарифы считались бы равными нулю. В случае превышения потребностей над запасами вводится фиктивный (m+1)-й поставщик с запасами, покрывающими потребности потребителей и равными нулю тарифами. При составлении начального опорного решения в последнюю очередь следует распределять запасы фиктивного поставщика и удовлетворять запросы фиктивного потребителя. 5.3. Построение начального опорного плана. Определение оптимального плана транспортной задачи начинают с нахождения какого-нибудь ее опорного плана. Опорный план находят последовательно за n+m-1 шагов, на каждом из которых в таблице условий задачи заполняют одну клетку, которую называют занятой. Заполнение одной из клеток обеспечивает полностью либо удовлетворение потребности в грузе одного из пунктов назначения, либо вывоз груза из одного из пунктов отправления. Опорный план является исходным условием для проверки последнего на оптимальность и нахождения оптимального плана. Рассмотрим три метода построения начального опорного плана. 1) Метод северо-западного угла: Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного X11 (“северо-западный угол”) Заканчивается для неизвестного Xmn, т. е. идет как бы по диагонали таблицы с севера на запад. Пример 1. Построим начальный опорный план для задачи (таблица 5.4) методом северо-западного угла и вычислим полученные затраты на перевозки. Таблица 5.4
Решение: Заполнение таблицы начнем с неизвестного x11, т. е. попытаемся удовлетворить потребности первого пункта назначения за счет запасов первого пункта отправления. Так как запасы пункта A1 меньше, чем потребности пункта B1, то полагаем x11=180, записываем это значение в соответствующей клетке таблицы и временно исключаем из рассмотрения строку А1, считая при этом потребности пункта В1 равными 20. Первые из оставшихся пунктов отправления A2 и назначения B1. Положим X21=20, запишем это значение в соответствующей клетке таблицы и временно исключим из рассмотрения столбец B1 и т.д. В результате получаем опорный план (таблица 5.5). Таблица 5.5
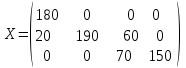 Общая стоимость перевозок всего груза Z=180∙10+20∙3+190∙7+60∙10+70∙5+150∙4=4740. 2) Метод минимального элемента: На каждом шаге следует выбирать какую-нибудь клетку, отвечающую минимальному тарифу (если таких клеток несколько, то следует выбирать любую из них), и рассмотреть пункты назначения и отправления, соответствующие выбранной клетке. Сущность метода минимального элемента и состоит в выборе клетки с минимальным тарифом. Этот метод, как правило, позволяет найти опорный план транспортной задачи, при котором общая стоимость перевозок груза меньше, чем общая стоимость перевозок при плане, найденном для данной задачи с помощью метода северо-западного угла. Поэтому более целесообразно опорный план транспортной задачи находить методом минимального элемента. Обратимся к примеру 1: минимальный тариф равный 1, находится в клетке для переменной x14. Положим x14=150, запишем это значение в соответствующую клетку таблицы и временно исключим из рассмотрения столбец В4. Запасы пункта А1 считаем равными 30. В оставшейся части таблицы с тремя строками A1, А2 и A3 и тремя столбцами B1, B2, B3 клетка с наименьшим тарифом находится на пересечении строки A1 и столбца B2, где минимальный тариф равен 2. Положим X12=30 и внесем это значение в соответствующую клетку. Временно исключим из рассмотрения строку А1 и будем считать запросы В2 равными 160. После этого рассмотрим оставшуюся часть таблицы с двумя строками A2 и A3 и тремя столбцами B1, B2 и B3. В ней находится минимальный тариф в клетке на пересечении строки A2 и столбца B1 и равен 3. Заполним описанным выше способом эту клетку и аналогично заполним оставшиеся клетки. В результате получаем опорный план (таблица 5.6): Таблица 5.6
Общая стоимость перевозок всего груза Z=3∙200+2∙30+7∙70+12∙90+130∙5+150∙1=3030. 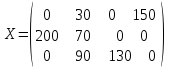 3) Метод аппроксимации Фогеля: На каждой итерации по всем столбцам и по всем строкам находят разность между двумя записанными в них минимальными тарифами. Разности записывают в специально отведенных для этого строке и столбце в таблице условий задачи. Среди разностей выбирают максимальную. В строке (или столбце), которой данная разность соответствует, определяют минимальный тариф. Клетку, в которой он записан, заполняют на данной итерации. Если минимальный тариф одинаков для нескольких клеток данной строки (столбца), то для заполнения выбирают ту клетку, которая расположена в столбце (строке), соответствующем наибольшей разности между двумя минимальными тарифами, находящимися в данном столбце (строке). Для каждой строки и столбца таблицы условий найдем разности между двумя минимальными тарифами, записанными в данной строе или столбце, и поместим их в соответствующем дополнительном столбце или строке (таблица 5.7). Таблица 5.7
Вычислив все эти разности, видим, что наибольшая из них соответствует столбцу B1. В этом столбце минимальный тариф записан в клетке, находящейся на пересечении строки A2 и столбца B1. Таким образом, эту клетку следует заполнить. Заполнив ее, тем самым мы удовлетворим потребности пункта B1. Поэтому исключим из рассмотрения столбец B1 и будем считать запасы пункта A2 равными 70. Заполним описанным выше способом эту клетку и аналогично заполним оставшиеся клетки. В результате получаем опорный план (таблица 5.8). Таблица 5.8
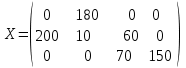 Общая стоимость перевозок всего груза Z=3∙200+2∙180+7∙10+60∙10+70∙5+150∙4=2580. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||