Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
10.2. Ошибки первого и второго рода. Статистический критерий проверки нулевой гипотезы. Выдвинутая гипотеза может быть правильной или неправильной, поэтому возникает необходимость ее проверки. Определение.Процедура сопоставления высказанной гипотезы с выборочными данными называется проверкой гипотезы. В итоге статистической проверки гипотезы в двух случаях может быть принято неправильное решение, т. е. могут быть допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Вероятность совершить ошибку первого рода принято обозначать через ; ее называют уровнем значимости. Наиболее часто уровень значимости принимают равным 0,05 или 0,01. Если, например, принят уровень значимости равный 0,05, то это означает, что в пяти случаях из ста мы рискуем допустить ошибку первого рода (отвергнуть правильную гипотезу). Вероятность допустить ошибку 2-го рода, принять гипотезу 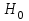 , когда она неверна, обычно обозначается β. , когда она неверна, обычно обозначается β. Определение. Вероятность (1-β) не допустить ошибку 2-го рода, опровергнуть гипотезу 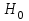 , когда она неверна, называется мощностью критерия. , когда она неверна, называется мощностью критерия.Статистический критерий проверки нулевой гипотезы. Проверка статистической гипотезы заключается в том, что используется специально составленная выборочная характеристика (статистика), полученная по выборке, точное или приближенное распределение которой известно. Эту величину обозначают через Uили Z, если она распределена нормально, Fили v2— по закону Фишера — Снедекора, Т — по закону Стьюдента, 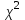 — по закону (хи квадрат) и т. д. — по закону (хи квадрат) и т. д. Определение. Статистическим критерием(или просто критерием) называют случайную величину, вычисленную по определенному правилу, служащую для проверки нулевой гипотезы. Определение. Наблюдаемым значениемназначают значение критерия, вычисленное по выборочным данным. 10.3. Критическая область. Область принятия гипотезы. Критические точки После выбора определенного критерия, множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другое — при которых она принимается. Определение. Критической областьюназывают совокупность значений критерия, при которых нулевую гипотезу отвергают. Определение. Областью принятия гипотезы(областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают. Определение. Критическими точками(границами) 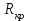 называют точки, отделяющие критическую область от области принятия гипотезы. называют точки, отделяющие критическую область от области принятия гипотезы.Различают одностороннюю (правостороннюю или левостороннюю) и двустороннюю критические области. Определение. Правостороннейназывают критическую область, определяемую неравенством 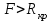 где гдеОпределение. Левосторонней называют критическую область, определяемую неравенством 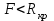 где где Односторонней называют правостороннюю или левостороннюю критическую область. Определение. Двустороннейназывают критическую область, определяемую неравенствами  , ,  , , 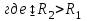 . .В частности, если критические точки симметричны относительно нуля, двусторонняя критическая область определяется неравенствами (в предположении, что 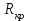 >0): >0):F<- 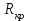 или F> или F>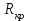 или равносильным неравенством или равносильным неравенством 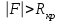 . . Критические точки находят по соответствующим таблицам. 10.4. Сравнение двух дисперсий нормальных генеральных совокупностей На практике задача сравнения дисперсий возникает, если требуется сравнить точность работы двух систем, самих методов принятия решений и т. д. Очевидно, предпочтительнее отдано той системе, которая обеспечивает наименьшее рассеяние результатов наблюдений, то есть наименьшую дисперсию. Пусть генеральные совокупности Xи Yраспределены нормально. По независимым выборкам объемов  и, и,  извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии  . Требуется по исправленным дисперсиям, при заданном уровне значимости a, проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: . Требуется по исправленным дисперсиям, при заданном уровне значимости a, проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: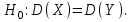 Учитывая, что исправленные дисперсии являются несмещенными оценками генеральных дисперсий, т. е. 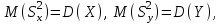 нулевую гипотезу можно записать так: 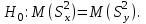 Для того чтобы, при заданном уровне значимости a, проверить нулевую гипотезу 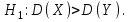 , надо вычислить отношение большей исправленной дисперсии к меньшей, т. е. , надо вычислить отношение большей исправленной дисперсии к меньшей, т. е.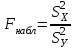 . (10.1) . (10.1)Величина F, при условии справедливости нулевой гипотезы имеет распределение Фишера—Снедекора со степенями свободы  , где , где  — объем выборки, по которой вычислена большая исправленная дисперсия, — объем выборки, по которой вычислена большая исправленная дисперсия,  — объем выборки, по которой найдена меньшая дисперсия. Распределение Фишера—Снедекора зависит только от числа степеней свободы и не зависит от других параметров. — объем выборки, по которой найдена меньшая дисперсия. Распределение Фишера—Снедекора зависит только от числа степеней свободы и не зависит от других параметров.По таблице критических точек распределения Фишера — Снедекора, по заданному уровню значимости a и числам степеней свободы  , и , и 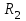 находят критическую точку находят критическую точку  Если  — нет оснований отвергнуть нулевую гипотезу. — нет оснований отвергнуть нулевую гипотезу.Если  — нулевую гипотезу отвергают. — нулевую гипотезу отвергают.Пример 1. По двум независимым выборкам объемов 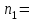 12 и п2=15,извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии 12 и п2=15,извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии 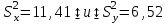 При уровне значимости 0,05, проверить нулевую гипотезу При уровне значимости 0,05, проверить нулевую гипотезу 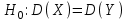 о равенстве генеральных дисперсий, при конкурирующей гипотезе о равенстве генеральных дисперсий, при конкурирующей гипотезе 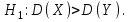 Решение. Найдем отношение большей исправленной дисперсии к меньшей:  Так как конкурирующая гипотеза имеет вид D(X)>D(Y), критическая область — правосторонняя. По таблице приложения, по уровню значимости a=0,05 и числам степеней свободы  =12-1=11 и =12-1=11 и 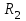 15-1=14, находим критическую точку 15-1=14, находим критическую точку 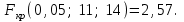 Так как Второй случай. Нулевая гипотеза 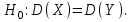 Конкурирующая гипотеза Конкурирующая гипотеза 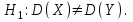 В этом случае строят двустороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область, в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости a. Если обозначить через F1, левую границу критической области и через F2— правую, то должны иметь место соотношения: 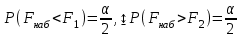 . .Наибольшая мощность критерия (вероятность попадания критерия в критическую область, при справедливости конкурирующей гипотезы) достигается тогда, когда «левая» и «правая» критические точки выбраны так, что вероятность попадания критерия в каждый из двух интервалов критической области, равна 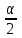 Область принятия нулевой гипотезы:  . .Для того чтобы, при заданном уровне значимости a проверить нулевую гипотезу о равенстве генеральных дисперсий нормально распределенных совокупностей, при конкурирующей гипотезе 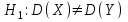 , надо вычислить отношение большей исправленной дисперсии к меньшей, т. е. , надо вычислить отношение большей исправленной дисперсии к меньшей, т. е. 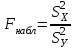 и по таблице критических точек распределения Фишера—Снедекора по уровню значимости и числам степеней свободы и по таблице критических точек распределения Фишера—Снедекора по уровню значимости и числам степеней свободы  и и 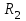 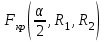 . .Если  — нет оснований отвергнуть нулевую гипотезу. Если — нет оснований отвергнуть нулевую гипотезу. Если  — нулевую гипотезу отвергают. — нулевую гипотезу отвергают.10.5. Сравнение двух средних нормальных генеральных совокупностей, дисперсии которых известны (независимые выборки) Пусть генеральные совокупности X и Y распределены нормально, причем их дисперсии известны (например, из предшествующего опыта, или найдены теоретически). По независимым выборкам объемов n и m, извлеченным из этих совокупностей, найдены выборочные средние  и и 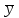 . .Требуется по выборочным средним, при заданном уровне значимости α, проверить нулевую гипотезу, состоящую в том, что генеральные средние (математические ожидания) рассматриваемых совокупностей равны между собой  . .В качестве критерия проверки нулевой гипотезы примем случайную величину 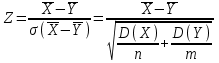 . (10.2) . (10.2)Эта величина случайная, потому что в различных опытах  и и 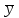 принимают различные, наперед неизвестные значения. принимают различные, наперед неизвестные значения.Критерий Z — нормированная нормальная случайная величина. Правило 1. Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу  о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями, при конкурирующей гипотезе о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями, при конкурирующей гипотезе 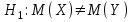 надо вычислить наблюденное значение критерия надо вычислить наблюденное значение критерия 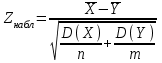 и по таблице функции Лапласа найти и по таблице функции Лапласа найтикритическую точку по равенству  . .Если 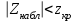 — нет оснований отвергнуть нулевую гипотезу. — нет оснований отвергнуть нулевую гипотезу.Если  — нулевую гипотезу отвергают. — нулевую гипотезу отвергают.Правило 2. Для того чтобы, при заданном уровне значимости α, проверить нулевую гипотезу  о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями, при конкурирующей гипотезе о равенстве математических ожиданий двух нормальных генеральных совокупностей с известными дисперсиями, при конкурирующей гипотезе  надо вычислить наблюденное значение критерия надо вычислить наблюденное значение критерия 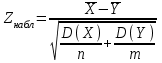 и по таблице функции Лапласа найти критическую точку из равенства и по таблице функции Лапласа найти критическую точку из равенства  . .Если 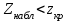 — нет оснований отвергнуть нулевую гипотезу. — нет оснований отвергнуть нулевую гипотезу.Если 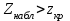 —нулевую гипотезу отвергают. —нулевую гипотезу отвергают. Пример 2. По двум независимым выборкам объемов n=10 и m10, извлеченным из нормальных генеральных совокупностей, найдены выборочные средние  и и 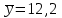 . Генеральные дисперсии известны: . Генеральные дисперсии известны:D(X)=22, D(Y)= 18. При уровне значимости 0,05, проверить нулевую гипотезу  , при конкурирующей гипотезе , при конкурирующей гипотезе  Решение. Найдем наблюдаемое значение критерия 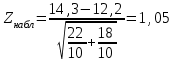 . .По условию конкурирующая гипотеза имеет вид M(X)>M(Y), поэтому критическая область — правосторонняя. По таблице функции Лапласа находим  . .Так как 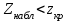 — нет оснований отвергнуть нулевую гипотезу. Другими словами, выборочные средние различаются незначимо. — нет оснований отвергнуть нулевую гипотезу. Другими словами, выборочные средние различаются незначимо.Правило 3. При конкурирующей гипотезе  надо вычислить надо вычислить  и сначала по таблице функции Лапласа найти «вспомогательную точку» и сначала по таблице функции Лапласа найти «вспомогательную точку»  по равенству по равенству  , а затем положить , а затем положить 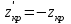 . .Если 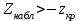 — нет оснований отвергнуть нулевую гипотезу. — нет оснований отвергнуть нулевую гипотезу.Если 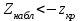 — нулевую гипотезу отвергают. — нулевую гипотезу отвергают.10.6. Критерием согласияназывают критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Имеется несколько критериев согласия: χ2, Пирсона, Колмогорова, Смирнова и др. Рассмотрим применение критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности (критерий аналогично применяется для других распределений, в этом состоит его достоинство). С этой целью будем сравнивать эмпирические (наблюдаемые) и теоретические (вычисленные в предположении нормального распределения) частоты. Обычно эмпирические и теоретические частоты различаются. Возможно, что расхождение случайно (незначимо) и объясняется малым числом наблюдений, либо способом их группировки, либо другими причинами. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены, исходя из неверной гипотезы о нормальном распределении генеральной совокупности. Критерий Пирсона отвечает на поставленный выше вопрос. Как и любой критерий, он не доказывает справедливость гипотезы, а лишь устанавливает, на принятом уровне значимости, ее согласие или несогласие с данными наблюдений. Пусть по выборке объема n получено эмпирическое распределение: варианты xi x1 x2 … xS эмп. частоты ni n1 n2 … nS Допустим, что в предположении нормального распределения генеральной совокупности, вычислены теоретические частоты n’i. При уровне значимости α, требуется проверить нулевую гипотезу; генеральная совокупность распределена нормально. В качестве критерия проверки нулевой гипотезы примем случайную величину:  Эта величина случайная, так как в различных опытах она принимает различные, заранее неизвестные значения. Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия (10.3). Доказано, что при n→∞ закон распределения случайной величины (10.3), независимо от того, какому закону распределения подчинена генеральная совокупность, стремится закону распределения χ2 с k степенями свободы. Поэтому случайная величина (*) обозначена через χ2, а сам критерий называют критерием согласия «хи квадрат». Число степеней свободы находят по равенству k=s-1-r, где s – число групп (частичных интервалов) выборки; r – число параметров предполагаемого распределения, которые оценены по данным выборки. В частности, если предполагаемое распределение — нормальное, то оценивают два параметра (математическое, ожидание и среднее квадратическое отклонение) r=2 и число степеней свободы k=s – 1 – r =s – 1 – 2 = s – 3. Если, например, предполагают, что генеральная cсовокупность распределена по закону Пуассона, то оценивают один параметр λ, поэтому r= 1 и k=s – 2. Поскольку односторонний критерий более «жестко» отвергает нулевую гипотезу, чем двусторонний, построим правостороннюю критическую область, исходя из требования, чтобы вероятность попадания критерия в эту область, в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости α: 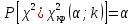 Таким образом, правосторонняя критическая область определяется неравенством: 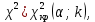 а область принятия нулевой гипотезы — неравенством 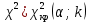 Обозначим значение критерия, вычисленное по данным наблюдений, через χ2набл сформулируем правило правило нулевой гипотезы. Правило. Для того чтобы, при заданном уровне значимости, проверить нулевую гипотезу Н0: генеральная совокупность распределена нормально, надо сначала вычислить теоретические частоты, а затем наблюдаемое значение критерия (10.3).  и по таблице критических точек распределения χ2, по заданному уровню значимости α, и числу степеней свободы k=s – 3, найти критическую точку χ2кр(α;k). Eсли 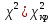 – нет оснований отвергнуть нулевую гипотезу. – нет оснований отвергнуть нулевую гипотезу.Если 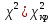 – нулевую гипотезу отвергают. – нулевую гипотезу отвергают. Объем выборки должен быть достаточно велик во всяком случае не менее 50. Каждая группа должна содержать не менее 5—8 вариант; малочисленные группы следует объединять в одну, суммируя частоты. В целях контроля вычислений, формулу преобразуют к виду 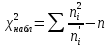 Для расчета теоретических частот можно использовать следующий алгоритм: 1. Весь интервал наблюдаемых значений Х (выборки объема п) делят на s частичных интервалов (xi, xi+1) одинаковой длины. Находят середины частичных интервалов 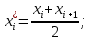 в качестве частоты ni варианты хi* примают число вариант, которые попали вi-й интервал. В итоге получают последовательность равноотстоящих вариант и соответствующих им частот: х1* , х2*, … , хs* n1 , n2, …ns причем Σni=n 2. Вычисляют, выборочную среднюю 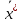 и выборочное среднее квадратическое отклонение σ*. и выборочное среднее квадратическое отклонение σ*.3. Нормируют случайную величину X, т. е. переходят к величине 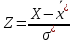 и вычисляют концы интервалов (zi, zi+1):   причем наименьшее значениеZ, т. е. z1 полагают равным - ∞, а наибольшее, т. е. zS полагают равным ∞. 4. Вычисляют теоретические вероятностиpi попадания X в интервалы(xi, xi+1) по равенству(Φ(z) — функция Лапласа) Pi= Φ(zi+1) – Φ(zi) и, наконец, находят искомые теоретические частоты n’i=npi. Глава 11. Корреляция и регрессия Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Yот одной или нескольких других величин. Рассмотрим зависимость Yот одной случайной (или неслучайной) величины X.. Две случайные величины могут быть связаны функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми. Строгая функциональная зависимость реализуется редко, так как обе величины или одна из них подвержены еще действию случайных факторов. Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статистическую зависимость называют корреляционной. 11.1. Условные средние. Корреляционная зависимость Предположим, что изучается связь между случайной величиной У и случайной величиной X. Пусть каждому значению X соответствует несколько значений У. Например, пусть при 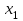 =2 величина У приняла значения: =2 величина У приняла значения: 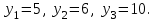 Найдем среднее арифметическое этих чисел: Найдем среднее арифметическое этих чисел: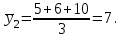 Число 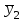 называют условным средним; черточка над буквой у служит обозначением среднего арифметического, а число 2 указывает, что рассматриваются те значения У, которые соответствуют называют условным средним; черточка над буквой у служит обозначением среднего арифметического, а число 2 указывает, что рассматриваются те значения У, которые соответствуют 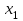 =2. =2.Условным средним 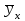 называют среднее арифметическое значений Y, соответствующих значению Х=х. называют среднее арифметическое значений Y, соответствующих значению Х=х.Если каждому значению х соответствует одно значение условной средней, то, очевидно, условная средняя есть функция от х; в этом случае говорят, что случайная величина У зависит от X корреляционно. Корреляционной зависимостью Y от X называют функциональную зависимость условной средней 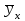 от х: от х: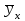 =f(x). (11.1). =f(x). (11.1).Уравнение (11.1) называют уравнением регрессии Yна X; функцию f(x) называют регрессией Y на X, а ее график — линией регрессии Yна X. Аналогично определяется условная средняя  , и корреляционная зависимость X от Y. , и корреляционная зависимость X от Y.Условным средним  называют среднее арифметическое значений X, соответствующих Y=y. называют среднее арифметическое значений X, соответствующих Y=y.Корреляционной зависимостью X от Y называют функциональную зависимость условной средней  от у: от у: =φ(у) (11.2). =φ(у) (11.2).Уравнение (11.2) называют уравнением регрессии Xна У; функцию φ(у)называют регрессией X на Y, а ее график — линией регрессии Xна У. Две основные задачи теории корреляции Первая задача теории корреляции — установить форму корреляционной связи, т. е. вид функции регрессии (линейная, квадратичная показательная и т. д.). Наиболее часто функции регрессии оказываются линейными. Если обе функции регрессии f(x) и φ(у)линейны, то корреляцию называют линейной; в противном случае — нелинейной. Очевидно, при линейной корреляции обе линии регрессии являются прямыми линиями. Вторая задача теории корреляции — оценить тесноту (силу) корреляционной связи. Теснота корреляционной зависимости Yот Xоценивается по величине рассеяния значений Yвокруг условного среднего 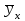 . Большое рассеяние свидетельствует о слабой зависимости У от Xлибо об отсутствии зависимости. Малое рассеяние указывает наличие достаточно сильной зависимости; возможно даже, что Yи Х связаны функционально, но под воздействием второстепенных случайных факторов эта связь оказалась размытой, в результате чего при одном и том же значении х величина Yпринимает различные значения. . Большое рассеяние свидетельствует о слабой зависимости У от Xлибо об отсутствии зависимости. Малое рассеяние указывает наличие достаточно сильной зависимости; возможно даже, что Yи Х связаны функционально, но под воздействием второстепенных случайных факторов эта связь оказалась размытой, в результате чего при одном и том же значении х величина Yпринимает различные значения.Аналогично (по величине рассеяния значений Xвокруг условного среднего  оценивается теснота корреляционной связи Xот У. оценивается теснота корреляционной связи Xот У.Отыскание параметров выборочного уравнения прямой линии регрессии по несгруппированным данным Допустим, что количественные признаки Xи Yсвязаны линейной корреляционной зависимостью. В этом случае обе линии регрессии будут прямыми. Предположим, что для отыскания уравнений этих прямых проведено п независимых испытаний, в результате которых получены п пар чисел:  Поскольку наблюдаемые пары чисел можно рассматривать как случайную выборку из генеральной совокупности всех возможных значений случайной величины (X, Y), то величины и уравнения, найденные по этим данным, называют выборочными. Для определенности будем искать выборочное уравнение прямой линии регрессии Y . Рассмотрим простейший случай: различные значения х признака Xи соответствующие им значения у признака Yнаблюдались по одному разу. Очевидно, что группировать данные нет необходимости. Также нет надобности использовать понятие условной средней, поэтому искомое уравнение 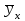 =kx+b =kx+bможно записать так: Y=kх+b. Угловой коэффициент прямой линии регрессии принято называть выборочным коэффициентом регрессии Yна Xи обозначать через 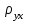 . . Итак, будем искать выборочное уравнение прямой линии регрессии вида: Y= 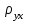 x+b. (11.3). x+b. (11.3).Поставим своей задачей подобрать параметры 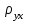 и bтак, чтобы точки и bтак, чтобы точки  построенные по данным наблюдений на плоскости XOYкак можно ближе лежали вблизи прямой (11.3). построенные по данным наблюдений на плоскости XOYкак можно ближе лежали вблизи прямой (11.3).Уточним смысл этого требования. Назовем отклонением разность 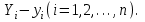 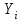 — вычисленная по уравнению (11.3) ордината, соответствующая наблюдаемому значению — вычисленная по уравнению (11.3) ордината, соответствующая наблюдаемому значению 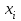 ; ;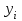 — наблюдаемая ордината, соответствующая — наблюдаемая ордината, соответствующая 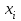 . .  Подберем параметры 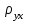 и bтак, чтобы сумма квадратов отклонений была минимальной (в этом состоит сущность метода наименьших квадратов). и bтак, чтобы сумма квадратов отклонений была минимальной (в этом состоит сущность метода наименьших квадратов). Так как каждое отклонение зависит от отыскиваемых параметров, то и сумма квадратов отклонений есть функция Fэтих параметров ( вместо 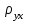 будем писать ρ): будем писать ρ): Для отыскания минимума приравняем нулю соответствующие частные производные: 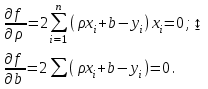 Выполнив элементарные преобразования, получим систему двух линейных уравнений относительно ρ ub.  (11.4) (11.4)Решив эту систему, найдем искомые параметры: 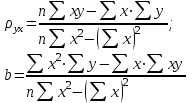 (11.5) (11.5)Аналогично можно найти выборочное уравнение прямой линии регрессии Xна У:  где  — выборочный коэффициент регрессии Х на У. — выборочный коэффициент регрессии Х на У. Пример. Найти выборочное уравнение прямой линии регрессии У на Xпо данным n=5 наблюдений: X 1,00 1,50 3,00 4,50 5,00; У 1,25 1,40 1,50 1,75 2,25. Решение. Составим расчетную таблицу 11.1. Таблица 11.1
Найдем искомые параметры, для чего подставим вычисленные по таблице суммы в соотношения (11.5):  Напишем искомое уравнение регрессии: Y=0,202x+1,024. Для того чтобы получить представление, насколько хорошо вычисленные по этому уравнению значения 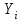 согласуются с наблюдаемыми значениями согласуются с наблюдаемыми значениями  , найдем отклонения , найдем отклонения 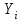 — — . Результаты вычислений сведены в таблицу 11.2. . Результаты вычислений сведены в таблицу 11.2.Таблица 11.2
Как видно из таблицы, не все отклонения достаточно малы. Это объясняется малым числом наблюдений. Для того, чтобы регрессионный анализ, основанный на методе наименьших квадратов, давал наилучшие результаты, должны выполняться следующие условия Гаусса-Маркова, которые используют для проверки качества модели: Математическое ожидание случайной составляющей в любом наблюдении должно быть равно нулю 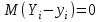 . Иногда случайная составляющая . Иногда случайная составляющая 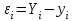 будет положительной, иногда отрицательной, но она не должна иметь систематического смещения ни в одном из двух возможных направлений. будет положительной, иногда отрицательной, но она не должна иметь систематического смещения ни в одном из двух возможных направлений. В модели зависимая переменная есть величины случайные, а независимая переменная – величина неслучайная. Если это условие выполнено, то теоретическая корреляция между независимой переменной и случайным членом (фактором) равна нулю. В любых наблюдениях отсутствует систематическая связь между значениями случайной составляющей 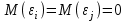 . Их значения должны быть независимы друг от друга в каждом наблюдениию. . Их значения должны быть независимы друг от друга в каждом наблюдениию. Дисперсия случайной составляющей должна быть постоянна для всех наблюдений 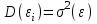 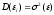 . . Предполагается нормальность распределения случайной составляющей или зависимой переменной. Это условие необходимо для оценки точности уравнения регрессии и его параметров. При большом числе наблюдений одно и то же значение может встретиться  раз, одно и то же значение у может встретиться раз, одно и то же значение у может встретиться 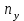 раз, одна и та же пара чисел (х, у) может наблюдаться раз, одна и та же пара чисел (х, у) может наблюдаться 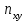 раз. Поэтому данные наблюдений группируют, т. е. подсчитывают частоты раз. Поэтому данные наблюдений группируют, т. е. подсчитывают частоты  , , 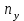 , , 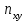 . Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной. . Все сгруппированные данные записывают в виде таблицы, которую называют корреляционной.Запишем систему (11.4) так, чтобы она отражала данные корреляционной таблицы. Воспользуемся тождествами:  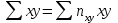 (учтено, что пара чисел (х, у) наблюдалось пхураз). (учтено, что пара чисел (х, у) наблюдалось пхураз).Подставив правые части тождеств в систему (11.4) и сократив обе части второго уравнения на п, получим: 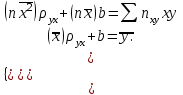 (11.6) (11.6)Решив эту систему, найдем параметры  и bи, следовательно, искомое уравнение: и bи, следовательно, искомое уравнение: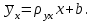 Однако более целесообразно, введя новую величину — коэффициент корреляции, написать уравнение регрессии ином виде. Найдем bиз второго уравнения (11.6):  Подставив правую часть этого равенства в уравнение 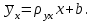 , получим: , получим: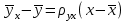 . (11.7) . (11.7)Найдем из_системы (11.4) коэффициент регрессии, учитывая, что 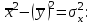 , ,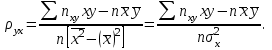 Умножим обе части равенства на дробь 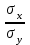 : :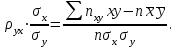 Обозначим правую часть равенства через 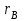 и назовем ее выборочным коэффициентом корреляции: и назовем ее выборочным коэффициентом корреляции:  или или  . .Подставив правую часть этого равенства в (11.6), окончательно получим выборочное уравнение прямой линии регрессии Yна Xвида 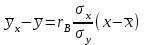 Аналогично находят выборочное уравнение прямой линии регрессии Xна Yвида 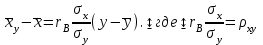 . .Выборочный коэффициент корреляции имеет важное самостоятельное значение. Как следует из предыдущего, выборочный коэффициент корреляции определяется равенством 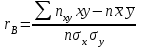 . .где х, у — варианты (наблюдавшиеся значения) признаков Xи Y 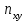 — частота наблюдавшейся пары вариант (х, у); — частота наблюдавшейся пары вариант (х, у);'п —объем выборки (сумма всех частот);  — выборочные средние; — выборочные средние; 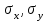 — выборочные средние квадратические отклонения — выборочные средние квадратические отклоненияВыборочный коэффициент корреляции служит для оценки тесноты линейной корреляционной зависимости. 1. Абсолютная величина выборочного коэффициента корреляции не превосходит единицы. 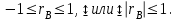 2. Если выборочный коэффициент корреляции равен нулю и выборочные линии регрессии — прямые, то X и У не связаны линейной корреляционной зависимостью. Если выборочный коэффициент корреляции равен нулю, то признаки X и Y могут быть связаны нелинейной корреляционной или даже функциональной зависимостью 3. Если абсолютная величина выборочного коэффициента корреляции равна единице, то наблюдаемые значения признаков связаны линейной функциональной зависимостью. 4. С возрастанием абсолютной величины выборочного коэффициента корреляции линейная корреляционная зависимость становится более тесной и при  =1 переходит в функциональную зависимость. =1 переходит в функциональную зависимость.Из приведенных свойств вытекает смысл 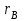 : выборочный коэффициент корреляции характеризует тесноту линейной связи между количественными признаками в выборке: чем ближе : выборочный коэффициент корреляции характеризует тесноту линейной связи между количественными признаками в выборке: чем ближе  к 1, тем связь сильнее; чем ближе к 1, тем связь сильнее; чем ближе к 0, тем связь слабее. к 0, тем связь слабее.Если выборка имеет достаточно большой объем и хорошо представляет генеральную совокупность (репрезентативна), то заключение о тесноте линейной зависимости между признаками, полученное по данным выборки, в известной степени может быть распространено и на генеральную совокупность. Например, для оценки коэффициента корреляции 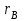 нормально распределенной генеральной совокупности (при n>50) можно воспользоваться формулой нормально распределенной генеральной совокупности (при n>50) можно воспользоваться формулой Знак выборочного коэффициента корреляции совпадает со знаком выборочных коэффициентов регрессии что следует из формул: 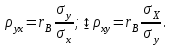 Выборочный коэффициент корреляции равен среднему геометрическому выборочных коэффициентов регрессии. Действительно, перемножив левые и правые части равенств (*) получим: 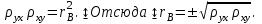 Знак при радикале, в соответствии с замечанием 1, должен совпадать со знаком коэффициентов регрессии Если график регрессии 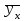 =f(x) или =f(x) или  =φ(у) изображается кривой линией, то корреляцию называют криволинейной. =φ(у) изображается кривой линией, то корреляцию называют криволинейной. Например, функции регрессии У на Xмогут иметь вид: 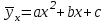 (параболическая корреляция второго порядка); (параболическая корреляция второго порядка); (параболическая корреляция третьего порядка); (параболическая корреляция третьего порядка); 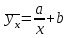 9. Сформулируйте теорему о вероятности произведения двух событий. 9. Сформулируйте теорему о вероятности произведения двух событий.10. Как (гиперболическая корреляция). Теория криволинейной корреляции решает те же задачи, что и теория линейной корреляции (установление формы и тесноты корреляционной связи). Контрольные вопросы к разделу 3. 1. Что называют событием? . Какие виды событий вы знаете? Дайте им определение. 2. Что называют полной группой событий? Чему равна сумма вероятностей событий, образующих полную группу? 3. Чему равна сумма вероятностей противоположных событий? 4. Сформулируйте формулу Байеса. Укажите когда она применяется. 5. Какими должны быть испытания, чтобы можно было применять формулу Бернулли? При каком условии используют теорему Пуассона? При каком условии используют теоремы Муавра–Лапласа? 6. Как вычисляются числовые характеристики дискретных и непрерывных случайных величин. 7. Какая задача решается с помощью критерия Пирсона? 8. Для чего служит выборочный коэффициент корреляции и в каких пределах он изменяется? Тестовые задания для самопроверки к разделу 3 1. Пусть вероятность для студента третьего курса дать правильный ответ на один вопрос равна 0,5. Тогда вероятность того, что из 5-ти предложенных студенту вопросов правильные ответы будут даны на 3 вопроса, равна 1. 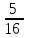 2. 0,3125 3. 2. 0,3125 3. 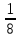 4. 4. 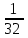 2. Случайная величина задана законом распределения:
Тогда Р(2) и математическое ожидание случайной величины  соответственно равны соответственно равны 1. 0,3 и 6 2. 0,4 и 4 3. 0,4 и 6,4 4. 0,6 и 5,76 3. Пусть событие  – попадание в цель при первом выстреле, – попадание в цель при первом выстреле, 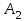 – попадание – попаданиев цель при втором выстреле. Тогда что означает событие 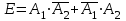 ? ?1. Попадание в цель хотя бы при одном выстреле 2. Попадание в цель только в одном выстреле 3. Попадание в цель при двух выстрелах 4. Попадание в цель не более одного раза 4. События А и В называются попарно независимыми, если 1. Р(А) = Р(В) 2. РВ(А) = Р(А); РА(В) = Р(В) 3. Р(А)+Р(В) = 1; 4. Р(АВ) = 0. 5. Сумма событий  происходит тогда, когда происходят: происходит тогда, когда происходят:1. И событие  , и событие , и событие 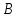 2. Либо событие  , либо событие , либо событие 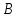 3. Либо событие  , либо событие , либо событие 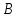 , либо оба вместе , либо оба вместе4. Только одно из этих двух событий ЗАКЛЮЧЕНИЕВ учебном пособии изложены теоретические основы дисциплины, приведены примеры решения типовых задач, представлены вопросы для самоконтроля, а также тестовые задания. Успешное овладение теоретическими основами дисциплины «Математика в экономике» позволит экономисту разрабатывать математические модели экономических процессов, приобрести необходимые базовые навыки для успешного освоения экономических и финансовых дисциплин. В целом при изложении материала применялись традиционные обозначения и терминология, что позволит студентам более свободно ориентироваться в терминах и определениях, а также способствует лучшему восприятию изучаемого теоретического материала В учебном пособии представлены основные вопросы программы курса дисциплины. Учебное пособие рекомендуется студентам очного и заочного обучения, с целью помочь им в подготовке к зачету, лекционным и практическим занятиям, выполнении домашних работ, контрольных. Использование учебного пособия в учебном процессе позволит сформировать у студентов базовые знания и навыки по данной дисциплине. БИБЛИОГРАФИЧЕСКИЙ СПИСОК 1. Антонов В.И., Лагунова М.В., Лобкова Н.И. Линейная алгебра и аналитическая геометрия: Опорный конспект: Учебное пособие. М.: Проспект, 2011. 2. Бортаковский А.С. Линейная алгебра в примерах и задачах: Учебное пособие – 2-е изд., стер. – («Прикладная математика для ВТУЗов). М.: Высшая школа, 2011. 3. Бугров, Я. С. Высшая математика в 3 т. Т. 2. Элементы линейной алгебры и аналитической геометрии : учебник для академического бакалавриата / Я. С. Бугров, С. М. Никольский. — 7-е изд., стер. — М. : Издательство Юрайт, 2017. «ЭБС ЮРАЙТ» 4. Бурмистрова. Е. Б. Линейная алгебра [Текст]: учебник и практикум для бакалавров / Е. Б. Бурмистрова, С. Г. Лобанов ; Нац. исслед. ун-т «Высш. шк. экономики». - М. : Юрайт, 2015. (ЭБ РТА). 5. Власов М. П., Шимко П. Д. Моделирование экономических систем и процессов: учеб. пособие. М.: ИНФРА-М, 2016. 336 с. 6. Гмуран, В.Е. Теория вероятностей и математическая статистика: [электронный ресурс]: учебник для прикладного бакалавриата / В.Е. Груман. – 12-е изд. – Электрон.копия печатного издания (файла: 91092 Кбайта). – М.: Юрайт, 2019. 7. Сборник задач по курсу «Математика в экономике». В 3-х ч. Ч.1 Линейная алгебра, аналитическая геометрия и линейное программирование: учебное пособие. М.: ИНФРА-М, ФиС, 2010. 8. Хуснутдинов Р. Ш. Экономико–математические методы и модели: учеб. пособие. М.: ИНФРА-М, 2017. 224 с. 9. Цвиль М. М. Математические методы и модели в управлении: учеб. пособие. Ростов н/Д.: Российская таможенная академия, Ростовский филиал, 2015. 221 с. 10. Цвиль М. М., Ширкунова Н.В., Ларькина Е.В. Математические модели в экономике: учеб. пособие. Ростов н/Д: Российская таможенная академия, Ростовский филиал, 2018. 210 с. |