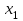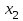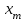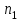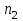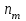Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
Пример 5. Нормально распределенная случайная величина Х задана своими параметрами – а =2 – математическое ожидание и = 1 – среднее квадратическое отклонение. Требуется написать плотность вероятности и построить ее график, найти вероятность того, Х примет значение из интервала (1; 3), найти вероятность того, что Х отклонится (по модулю) от математического ожидания не более чем на 2. Плотность распределения имеет вид: 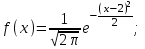 Построим график: 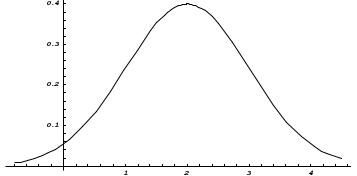 Найдем вероятность попадания случайной величины в интервал (1; 3). 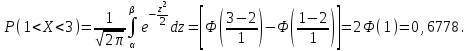 z zНайдем вероятность отклонение случайной величины от математического ожидания на величину, не большую чем 2. 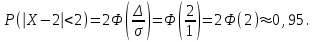 Тот же результат может быть получен с использованием нормированной функции Лапласа. Равномерное распределение Определение. Непрерывная случайная величина имеет равномерное распределение на отрезке [a, b], если на этом отрезке плотность распределения случайной величины постоянна, а вне его равна нулю. 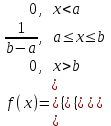 (8.17) (8.17)Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения.  f(x) f(x)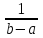 0 abx Рисунок 8.9. Функция плотности распределения. Найдем функцию распределения F(x) на отрезке [a,b]. 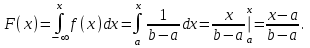 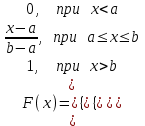 F(x) 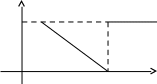 1 0 abx Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения. 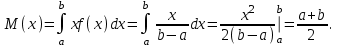 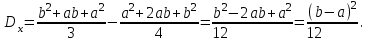 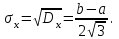 Вероятность попадания случайной величины в заданный интервал: 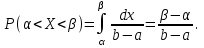 (Студентам предлагается самостоятельно изучить показательное распределение.) 8.5. Закон больших чисел и центральная предельная теорема теории вероятностей. На практике сложно сказать какое конкретное значение примет случайная величина, однако, при воздействии большого числа различных факторов поведение случайных величин практически утрачивает случайный характер. При изучении результатов наблюдений над реальными случайными массовыми явлениями имеют место некоторые закономерности. Они обладают свойством устойчивости. Это основано на том, что конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате большой массы подобных явлений, а характеристики случайных событий и случайных величин при неограниченном увеличении числа испытаний становятся практически не случайными. Этот факт очень важен на практике, так как позволяет предвидеть результат опыта при воздействии большого числа случайных факторов. Предельные теоремы вероятностей устанавливают зависимость между случайностью и необходимостью. По смыслу их можно разбить на две группы, одна из которых называется законом больших чисел, а другая —центральной предельной теоремой. Неравенство Чебышева. (Чебышев Пафнутий Львович (1821 – 1894) – русский математик Теорема 8.6. Для любой случайной величины Х, имеющей дисперсию D(X), при любом >0 справедливо неравенство 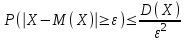 Неравенство позволяет оценить вероятность того, что отклонение случайной величины от ее математического ожидания не превышает по абсолютной величине положительного числа 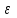 . Если . Если 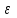 достаточно мало, то мы оценим, таким образом, вероятность того, что X примет значения, достаточно близкие к своему математическому ожиданию. Справедлива так же теорема, определяющая вероятность противоположного события. достаточно мало, то мы оценим, таким образом, вероятность того, что X примет значения, достаточно близкие к своему математическому ожиданию. Справедлива так же теорема, определяющая вероятность противоположного события.Теорема 8.7. Вероятность того, что отклонение случайной величины Х от ее математического ожидания по абсолютной величине меньше положительного числа e, не меньше чем 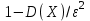 . .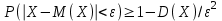 (8.18) (8.18)С помощью этого неравенства доказываются теоремы и делаются практические выводы. Теорема Чебышева Теорема 8.8. Если Х1, Х2, …, Хn- попарно независимые случайные величины, имеющие математическое ожидание М(Х1), М(Х2), М(Хп) причем дисперсии их равномерно ограничены (не превышают постоянного числа С), то, как бы мало не было положительное число , вероятность неравенства 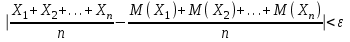 (8.19) (8.19)будет сколь угодно близка к единице, если число случайных величин достаточно велико. 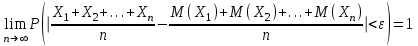 Если случайные величины имеют одно и то же математическое ожидание, то теорема Чебышева несколько упрощается: 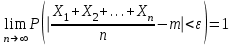 (8.20) (8.20)Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий. Теорема Бернулли Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равно р. Теорема дает возможность, оценить приблизительно относительную частоту появления события А. Теорема 8.9. Если в каждом из п независимых испытаний вероятность р появления события А постоянно, то сколь угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний р достаточно велико. 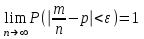 (8.21) (8.21)Центральная предельная теорема Суммирование большого числа случайных величин с самыми разными законами распределения приводит к тому, что результирующая случайная величина приближается к нормальному распределению. Указанное свойство подтверждается доказанной русским математиком Ляпуновым (1857-1918) интегральной предельной теоремой. Теорема 8.10. Если случайная величина Х представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, все величины имеют конечные математические ожидания и дисперсии, то случайная величина Х имеет распределение, близкое к нормальному. На практике для большинства случайных величин выполняются условия теоремы Ляпунова. Центральная предельная теорема имеет огромное значение для практики. При достаточно большом количестве испытаний, поставленных в одинаковых условиях, характеристики случайных событий и случайных величин становятся почти неслучайными. Это позволяет использовать результаты наблюдений случайных событий для предсказания исхода того или иного опыта. Однако следует иметь в виду, что при усилении влияния отдельных факторов могут появляться отклонения от нормального распределения результирующего параметра, например может возникать асимметрия или эксцесс. Поэтому большое значение на практике уделяется экспериментальной проверке выдвинутых гипотез, в том числе и гипотезы о нормальном распределении. Частным случаем центральной предельной теоремы для дискретных случайных величин являются теоремы Лапласа. Глава 9. Основные понятия математической статистики. Статистические оценки параметров распределения 9.1 Понятие генеральной совокупности. Математическая статистика — наука, изучающая методы обработки результатов наблюдений массовых случайных явлений, обладающих статистической устойчивостью, закономерностью, с целью выявления этой закономерности. Предметом математической статистики является изучение случайных величин (или случайных событий) по результатам наблюдений. Математическая статистика опирается на результаты наблюдений случайных явлений. Для изучения совокупности может проводится сплошное обследование, то есть обследуют каждый из объектов совокупности относительно изучаемого признака. На практике, однако, сплошное обследование применимо не всегда. Например, если совокупность содержит очень большое число объектов, или обследование объекта связано с его уничтожением, требуются большие материальные затраты, то проводить сплошное обследование практически не рационально. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению. Определение. Выборочной совокупностью, или просто выборкой,называют совокупность случайно отобранных объектов. Определение. Генеральной совокупностьюназывают совокупность объектов, из которых производится выборка. Определение. Объемомсовокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деклараций отобрано для обследования 100, то объем генеральной совокупности N=1000, а объем выборки п= 100. Генеральную совокупность будем называть конечной или бесконечной в зависимости от того, конечна или бесконечна совокупность составляющих ее элементов. При составлении выборки можно поступить двумя способами: после того, как объект отобран и над ним произведено наблюдение, он либо возвращается, либо не возвращен в генеральную совокупность. В соответствии с этим, выборки подразделяют на повторные и бесповторные. Определение. Повторнойназывают выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. Определение. Бесповторнойназывают выборку, при которой отобранный объект в генеральную совокупность не возвращается. На практике обычно пользуются бесповторным случайным отбором. Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем нас признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли. Это требование коротко формулируют так: выборка должна быть репрезентативной (представительной). В силу закона больших чисел можно утверждать, что выборка будет репрезентативной, если ее осуществить случайно: каждый объект выборки отобран случайно из генеральной совокупности, если все объекты имеют одинаковую вероятность попасть в выборку. Если объем генеральной совокупности достаточно велик, а выборка составляет лишь незначительную часть этой совокупности, то различие между повторной и бесповторной выборками стирается; в предельном случае, когда рассматривается бесконечная генеральная совокупность, а выборка имеет конечный объем, это различие исчезает. Способы отбора На практике применяются различные способы отбора. Принципиально эти способы можно подразделить на два вида: 1. Отбор, не требующий расчленения генеральной совокупности на части: а) простой случайный бесповторный отбор; б) простой случайный повторный отбор. 2. Отбор, при котором генеральная совокупность разбивается на части: а) типический отбор; б) механический отбор; в) серийный отбор. 9.2. Вариационный ряд. Графическое изображение вариационных рядов. Эмпирическая функция распределения выборки Полученные наблюдаемые значения признака представляют собой совокупность чисел, расположенных в беспорядке. Для изучения закономерностей случайной величины опытные данные подвергают обработке. Определение. Расположение значений случайной величины в порядке не убывания, называется ранжированием опытных данных. После проведения операции ранжирования опытные данные нетрудно объединить в группы. Пусть из генеральной совокупности извлечена выборка, объема п. Причем значение x1наблюдалось п1, раз, х2 — п2 раз, xk— nkраз. Определение. Значение случайной величины, соответствующее отдельной группе сгруппированного ряда наблюдаемых данных, называется вариантом, а изменение этого значения — варьированием. Варианты будем обозначать малыми буквами латинского алфавита с соответствующими порядковому номеру группы индексами хi,, где 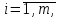 . .Определение. Число, которое показывает, сколько раз встречается соответствующий вариант в выборочной совокупности, называют частотой вариантаи обозначают nk, где i—индекс варианта. Определение. Отношение частоты данного варианта к общей сумме частот всех вариантов называется частостью fk или относительной частотой. 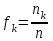 (9.1) (9.1)Представив варианты и соответствующие им частоты или относительные частоты в виде таблицы, получают вариационный ряд. Определение. Вариационным рядомназывается ряд статистических данных, представляющих собой наблюдаемые значения изучаемого признака Х, расположенных в порядке их возрастания или убывания, и соответствующие им частоты (или частости). Вариационный ряд называют так же частотным рядом распределения. В зависимости от того, какой величиной является изучаемый признак (дискретной или непрерывной), различают дискретные и непрерывные вариационные ряды. В общем виде вариационный ряд задается в виде таблицы. Определение. Дискретным вариационным рядом распределения называется ранжированная совокупность вариантов xk с соответствующими им частотами nk или частостями fk.
Определение. Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с соответствующими частотами или частостями попаданий в каждый из них значений величины.
В целях наглядности строят различные графики статистического распределения и, в частности, полигон и гистограмму. Определение. Полигоном частотназывают ломаную, отрезки которой соединяют последовательно точки (x1, п1), (х2, п2), ..., (xk, пк). Для построения полигона частот на оси абсцисс откладывают варианты xk, а на оси ординат — соответствующие им частоты пкТочки (xk, пк) соединяют последовательными отрезками.
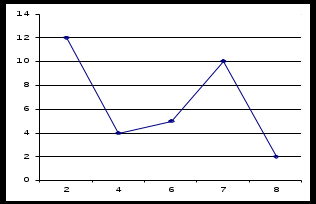 Полигоном относительных частот называют ломаную, отрезки которой соединяют точки (x1,fk), (х2, f2), ..., (хк, fk). Для построения полигона относительных частот на оси абсцисс откладывают варианты хк, а на оси ординат соответствующие им относительные частоты fk. Точки (хк,fk)соединяют отрезками и получают полигон относительных частот. Если возможные значения признака принадлежат интервалу (а;b), то целесообразно строить гистограмму частот (гистограмму частостей). Определение.Гистограммой частотназывают ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны частоте (частостям или плотности частоты п2/h) |