Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
9.3. Эмпирическая функция распределения Пусть известно статистическое распределение частот количественного признака X. Обозначим: пх— число наблюдений, при которых наблюдалось значение признака меньшее х, п — общее число наблюдений (объем выборки). Относительная частота события Х<х равна — пх/п. Определение. Эмпирической функцией распределения(функцией распределения выборки) называют функцию F*(x), определяющую для каждого значения х относительную частоту события Х<х. По определению 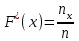 (9.2) (9.2)Таким образом, для того чтобы найти, например F*(x2), надо число вариант, меньших х2, разделить на объем выборки: 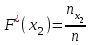 В отличие от эмпирической функции распределения выборки, интегральную функцию F(x) распределения генеральной совокупности называют теоретической функцией распределения. Различие между эмпирической и теоретической функциями состоит в том, что теоретическая функция F(x) определяет вероятность события Х<.х, а эмпирическая функция F*(x) определяет относительную частоту появления события в проведенных испытаниях. Из теоремы Бернулли следует, что относительная частота события Х<х, т. е. F*(x) стремится по вероятности к вероятности F(x) этого события. Поэтому можно использовать эмпирическую функцию распределения выборки для приближенного представления теоретической (интегральной) функции распределения генеральной совокупности. ФункцияF*(x) обладает всеми свойствами F(x). Свойства эмпирической функции распределения 1) значения эмпирической функции принадлежат отрезку [0,1]; 2) F*(x) — неубывающая функция; 3) если x1— наименьшая варианта, то F*(x)=0 при 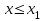 . .если xk— наибольшая варианта, то F*(x)=1 при x>xk. Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения генеральной совокупности. Если на оси Ох отложить значения вариант дискретного ряда, а по оси Оу накопленные частости, полученные точки последовательно соединить отрезками, то полученный график функции называют кумулятивной кривой. 9.4. Числовые характеристики случайной выборки Для изучения генеральной совокупности относительно количественного признака X извлечена выборка объема n. Определение. Выборочной средней 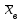 называют среднее арифметическое значение признака выборочной совокупности. называют среднее арифметическое значение признака выборочной совокупности. Если все значения 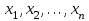 признака выборки объема n различны, то выборочная средняя рассчитывается по средней арифметической простой признака выборки объема n различны, то выборочная средняя рассчитывается по средней арифметической простой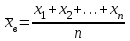 . (9.3) . (9.3)Если же значения признака 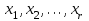 . имеют соответственно частоты . имеют соответственно частоты 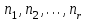 , то выборочная средняя рассчитывается по средней арифметической взвешенной , то выборочная средняя рассчитывается по средней арифметической взвешенной  (9.4) (9.4)Для того чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки вокруг своего среднего значения 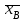 вводят сводную характеристику — выборочную дисперсию. вводят сводную характеристику — выборочную дисперсию.Определение. Выборочной дисперсией DB называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения 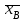 . .Если все значения 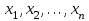 признака выборки объема n различны, то применяется формула признака выборки объема n различны, то применяется формула 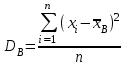 . (9.5) . (9.5)Если же значения признака 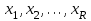 имеют соответственно частоты имеют соответственно частоты 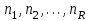 причем причем 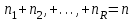 , то расчет, удобно проводит по формуле: , то расчет, удобно проводит по формуле: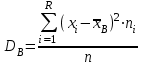 (9.6) (9.6)Пример 1. Выборочная совокупность задана таблицей распределения 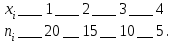 Найти выборочную дисперсию. Решение. Найдем выборочную среднюю: 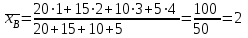 . . Найдем выборочную дисперсию: 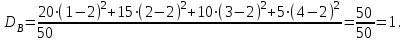 Кроме дисперсии, для характеристики рассеяния значений признака выборочной совокупности вокруг своего среднего значения пользуются сводной характеристикой — средним квадратическим отклонением. Выборочным средним квадратическим отклонением (стандартом) называют квадратный корень из выборочной дисперсии: 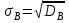 . (9.7) . (9.7)Вычисление выборочной дисперсии можно упростить, используя свойство дисперсии. Теорема 1. Дисперсия равна разности между средним значением квадратов значений признака и квадратом среднего значения признака 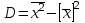 . (9.8) . (9.8)Вычислим дисперсию ранее рассмотренного примера по данной теореме. (Студентам предлагается самостоятельно изучить свойства среднего значения и свойства дисперсии. Сравнить их со свойствами математического ожидания) Определение. Коэффициентом вариации V называют выраженное в процентах отношение выборочного среднего квадратического отклонения к выборочной средней: 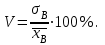 Коэффициент вариации служит для сравнения величин рассеяния двух вариационных рядов: тот из рядов имеет большее рассеяние, у которого коэффициент вариации больше. Гистограмма строится только для интервальных вариационных рядов и представляет собой ступенчатую фигуру из прямоугольников с основаниями, равными интервалам значений признака, и высотами, равными частотам интервалов. Если соединить середины верхних оснований прямоугольников отрезками прямой, то можно получить полигон распределения. 9.5. Понятие статистической оценки. Свойства точечных оценок. Для решения практических задач требуется изучить количественный признак генеральной совокупности. Из теоретических соображений удалось установить, какое распределение имеет признак. Возникает необходимость в оценке параметров, которыми определяется это распределение. Например, если установлено, что изучаемый признак распределен в генеральной совокупности нормально, то необходимо оценить (приближенно найти) математическое ожидание и среднеквадратическое отклонение, так как эти два параметра полностью определяют нормальное распределение. Приближенные значения параметров 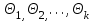 распределения, рассчитанные по результатам наблюдения (по собранной исследователем статистике), являются статистическими оценками параметров. распределения, рассчитанные по результатам наблюдения (по собранной исследователем статистике), являются статистическими оценками параметров.Определение.Выборочная характеристика, используемая в качестве приближенного значения неизвестной генеральной характеристики, называется ее точечной статистической оценкой. Точечная оценка означает, что оценка представляет собой некоторое число. Пусть 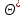 есть статистическая оценка неизвестных параметров теоретического распределения. Допустим, что по выборке объема n найдена оценка есть статистическая оценка неизвестных параметров теоретического распределения. Допустим, что по выборке объема n найдена оценка 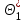 . Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку . Повторим опыт, т. е. извлечем из генеральной совокупности другую выборку того же объема и по ее данным найдем оценку 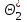 . Повторяя опыт многократно, получим числа . Повторяя опыт многократно, получим числа 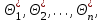 которые, вообще говоря, будут различны между собой. Таким образом, оценку которые, вообще говоря, будут различны между собой. Таким образом, оценку 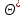 можно рассматривать как случайную величину, а числа можно рассматривать как случайную величину, а числа 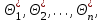 — как ее возможные значения. Так как параметр — как ее возможные значения. Так как параметр 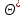 есть случайная величина, то можно говорить о ее математическом ожидании и дисперсии. Интерпретация оценки как случайной величины позволяет сформулировать свойства, которыми должно обладать оценка, чтобы ее можно было считать хорошим приближением к неизвестной генеральной характеристике. есть случайная величина, то можно говорить о ее математическом ожидании и дисперсии. Интерпретация оценки как случайной величины позволяет сформулировать свойства, которыми должно обладать оценка, чтобы ее можно было считать хорошим приближением к неизвестной генеральной характеристике.Свойства точечных оценок Определение. Несмещенной называют статистическую оценку 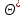 , математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, т. е. , математическое ожидание которой равно оцениваемому параметру при любом объеме выборки, т. е.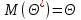 (9.9) (9.9)Смещенной называют точечную оценку Q*, математическое ожидание которой не равно оцениваемому параметру Q. Определение.Эффективнойназывают точечную оценку Q*, которая при заданном объеме выборки n имеет наименьшую дисперсию: если 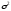 ( (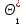 )< )<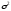 ( (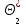 ), то оценка ), то оценка 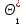 – эффективная оценка параметра – эффективная оценка параметра 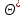 . .При рассмотрении выборок большого объема (n велико!) к статистическим оценкам предъявляется требование состоятельности. Определение. Состоятельной называют точечную оценку, которая при n стремится по вероятности к оцениваемому параметру. Например, если дисперсия несмещенной оценки при n стремится к нулю, то такая оценка оказывается и состоятельной. Оценка генеральной средней и генеральной дисперсии Изучению подвергается генеральная совокупность относительно количественного признака X. Определение. Генеральной средней 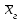 называют среднее арифметическое значений признака генеральной совокупности. называют среднее арифметическое значений признака генеральной совокупности. Если все значения 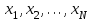 признака генеральной совокупности объема N различны, то признака генеральной совокупности объема N различны, то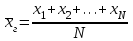 . (9.10) . (9.10)Если же значения признака 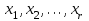 имеют соответственно частоты имеют соответственно частоты 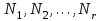 , причем , причем 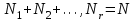 , то генеральная средняя рассчитывается по формуле , то генеральная средняя рассчитывается по формуле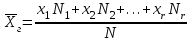 (9.11) (9.11)Для того чтобы охарактеризовать рассеяние значений количественного признака X генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию. Определение. Генеральной дисперсией D, называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения 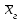 . . Если все значения 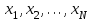 признака генеральной совокупности объема N различны, то признака генеральной совокупности объема N различны, то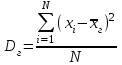 . (9.12) . (9.12)Если же значения признака 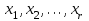 имеют соответственно частоты имеют соответственно частоты 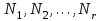 , причем , причем 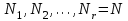 , то генеральная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам. , то генеральная дисперсия есть средняя взвешенная квадратов отклонений с весами, равными соответствующим частотам.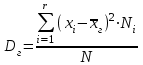 . (9.13) . (9.13)Кроме дисперсии, для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются характеристикой — средним квадратическим отклонением. Определение. Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии: 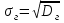 (9.14) (9.14)Практика показывает, что чаще всего при изучении генеральная совокупность относительно количественного признака X нам неизвестны все значения признака, в связи с этим рассчитать числовые характеристики (параметры) генеральной совокупности невозможно. Поэтому используют оценки этих параметров по данным выборки. Пусть из генеральной совокупности (в результате независимых наблюдений над количественным признакам X) извлечена выборка объема п со значениями признака 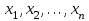 . Пусть генеральная средняя . Пусть генеральная средняя 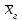 неизвестна и требуется оценить ее по данным выборки. В качестве оценки генеральной средней принимают выборочную среднюю. Выборочная средняя арифметическая неизвестна и требуется оценить ее по данным выборки. В качестве оценки генеральной средней принимают выборочную среднюю. Выборочная средняя арифметическая 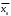 является несмещенной, состоятельной и эффективной оценкой генеральной средней. Можно показать, что является несмещенной, состоятельной и эффективной оценкой генеральной средней. Можно показать, что 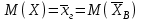 . .Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к систематическим ошибкам, давая заниженное значение генеральной дисперсии. Объясняется это тем, что выборочная дисперсия является смещенной оценкой Dг, то есть математическое ожидание выборочной дисперсии не равно оцениваемой генеральной дисперсии, а равно 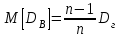 . . Легко «исправить» выборочную дисперсию так, чтобы ее математическое ожидание было равно генеральной дисперсии. Достаточно для этого умножить DB на дробь 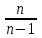 . .Исправленная дисперсия s2 является несмещенной оценкой генеральной дисперсии : 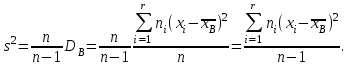 (9.15) (9.15)Для оценки среднего квадратического отклонения генеральной совокупности используют «исправленное» среднее квадратическое отклонение, которое равно квадратному корню из исправленной дисперсии: 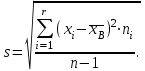 (9.16) (9.16)Сравнивая формулы 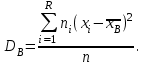 и и 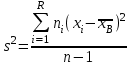 Можно заметить, что они отличаются лишь знаменателями. Очевидно, при достаточно больших значениях п объема выборки, выборочная и исправленная дисперсия различаются мало. На практике пользуются исправленной дисперсией, если примерно п < 30. 9.6. Интервальные оценки. Понятие доверительного интервала Все оценки, рассмотренные выше — точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т. е. приводить к. грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками. Определение. Интервальной называют оценку, которая определяется двумя числами- концами интервала, покрывающего оцениваемый параметр Θ. Пусть, найденная по данным выборки, статистическая характеристика 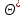 служит оценкой неизвестного параметра Θ. Будем считать Θ постоянным числом. Ясно, что служит оценкой неизвестного параметра Θ. Будем считать Θ постоянным числом. Ясно, что 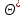 тем точнее определяет параметр Θ, чем меньше абсолютная величина разности тем точнее определяет параметр Θ, чем меньше абсолютная величина разности 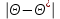 . Другими словами, если >0 и . Другими словами, если >0 и 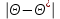 <, то, чем меньше , тем оценка точнее. Таким образом, положительное число характеризует точность оценки. <, то, чем меньше , тем оценка точнее. Таким образом, положительное число характеризует точность оценки.Однако статистические методы не позволяют категорически утверждать, что оценка 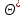 удовлетворяет неравенству удовлетворяет неравенству 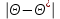 <; можно лишь говорить о вероятности γ, с которой это неравенство осуществляется. <; можно лишь говорить о вероятности γ, с которой это неравенство осуществляется.Определение. Надежностью (доверительной вероятностью) оценки Θ по 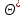 называют вероятность γ, с которой осуществляется неравенство называют вероятность γ, с которой осуществляется неравенство 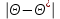 < < Обычно надежность оценки задается наперед, причем в качестве γ берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999. Пусть вероятность того, что 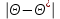 < равна γ: < равна γ: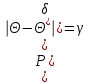 . .Заменив неравенство 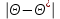 < равносильным ему двойным неравенством < равносильным ему двойным неравенством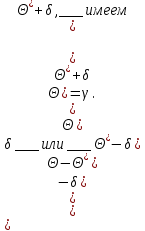 Это соотношение следует понимать так: вероятность того, что интервал ( 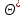 - , - , 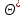 +) заключает в себе (покрывает) неизвестный параметр Θ, равна γ. +) заключает в себе (покрывает) неизвестный параметр Θ, равна γ.Определение. Доверительным называют интервал ( 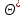 - , - , 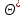 + ), который покрывает неизвестный параметр с заданной надежностью γ. + ), который покрывает неизвестный параметр с заданной надежностью γ. Интервал ( 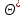 - , - , 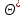 +) имеет случайные концы (их называют доверительными границами). +) имеет случайные концы (их называют доверительными границами). Доверительные интервалы для оценки математического ожидания нормального распределения при известном а. Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение σ этого распределения известно. Требуется оценить неизвестное математическое ожидание апо выборочной средней 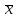 . . С надежностью γ можно утверждать, что доверительный интервал 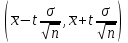 покрывает неизвестный параметр а, точность оценки 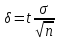 . .Число t определяется из равенства 2Ф(t)=γ, или Ф(t)= 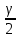 ; по таблице функции Лапласа находят аргумент t, которому соответствует значение функции Лапласа, равное ; по таблице функции Лапласа находят аргумент t, которому соответствует значение функции Лапласа, равное 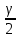 . .Глава 10. Проверка статистических гипотез 10.1. Понятие статистической гипотезы. Нулевая и конкурирующая, простая и сложная гипотезы. Пред исследователем стоит задача определить закон распределения генеральной совокупности. Если закон распределения неизвестен, но имеются основания предположить, что он имеет определенный вид, выдвигают гипотезу: генеральная совокупность распределена по закону Н. Таким образом, в этой гипотезе речь идет о виде предполагаемого распределения. Перед исследователем может стоять другая задача: закон распределения известен, а его параметры неизвестны. Если есть основания предположить, что неизвестный параметр Θ равен определенному значению 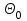 , выдвигают гипотезу: Н = , выдвигают гипотезу: Н =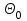 .- Таким образом, в этой гипотезе речь идет о предполагаемой величине параметра одного известного распределения. .- Таким образом, в этой гипотезе речь идет о предполагаемой величине параметра одного известного распределения.Определение.Статистическойгипотезой называют всякое высказывание о генеральной совокупности (о виде неизвестного распределения или о параметрах известных распределений), случайной величине, проверяемое по выборки (по результатам наблюдения). Например, статистическими будут гипотезы: 1) генеральная совокупность распределена по закону Пуассона; 2) дисперсии двух нормальных совокупностей равны между собой. Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза. По этой причине эти гипотезы целесообразно различать. Нулевой (основной) называют выдвинутую гипотезу 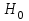 . .Конкурирующей (альтернативной) называют гипотезу 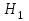 , которая противоречит нулевой. , которая противоречит нулевой.Например, если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 10, то конкурирующая гипотеза, в частности, может состоять в предположении, что а≠10. Коротко это записывают так: 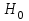 : а=10; : а=10; 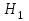 : а≠10. : а≠10.Различают гипотезы, которые содержат только одно и более одного предположений. Определение.Простойназывают гипотезу, содержащую только одно предположение. Например, если 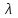 — параметр показательного распределения, то гипотеза — параметр показательного распределения, то гипотеза 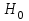 : : 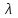 =5 — простая. =5 — простая. Гипотеза 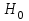 : математическое ожидание нормального распределения равно 3 (σ известно) — простая. : математическое ожидание нормального распределения равно 3 (σ известно) — простая.Определение. Сложнойназывают гипотезу, которая состоит из конечного или бесконечного числа простых гипотез. Например, сложная гипотеза Н: 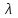 >5 состоит из бесчисленного множества простых вида >5 состоит из бесчисленного множества простых вида 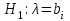 , где , где 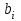 — любое число, большее 5. Гипотеза — любое число, большее 5. Гипотеза 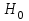 : математическое ожидание нормального распределения равно 3 (σ неизвестно) — сложная. : математическое ожидание нормального распределения равно 3 (σ неизвестно) — сложная. |
