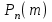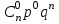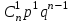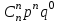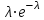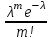Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
Найти математическое ожидание случайной величины. Решение. Математическое ожидание случайной величины равно: 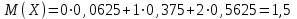 Определение. Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл 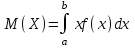 (8.6) (8.6)Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле: 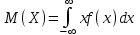 При этом, конечно, предполагается, что несобственный интеграл сходится. Свойства математического ожидания 1) Математическое ожидание постоянной величины равно самой постоянной. 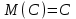 2) Постоянный множитель можно выносить за знак математического ожидания. 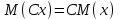 3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий. 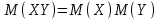 Это свойство справедливо для произвольного числа случайных величин. Случайные величины называются взаимно независимыми, если закон распределения любой из них не зависит от того, какие значения приняли какие- либо другие, рассматриваемые величины. 4) Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий слагаемых. 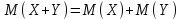 Это свойство также справедливо для произвольного числа случайных величин. 5) Математическое ожидание отклонения 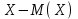 случайной величины Х от ее математического ожидания случайной величины Х от ее математического ожидания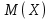 равно нулю равно нулю 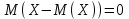 Пусть производится п независимых испытаний, вероятность появления события А в которых равна р. Справедлива следующая теорема. Теорема 8.2. Математическое ожидание М(Х) числа появления события А в п независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании. 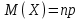 Математическое ожидание не может полностью характеризовать случайный процесс. На практике часто необходимо оценить рассеивание возможных значений случайной величины от математического ожидания. Определение. Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания. 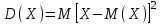 (8.7) (8.7)Если непрерывная случайная величина Х задана функцией распределения f(x) и все возможные значения случайной величины принадлежат отрезку [a,b], то дисперсия рассчитывается следующим образом. Теорема 8.3. Дисперсия равна разности между математическим ожиданием квадрата случайной величины Х и квадратом ее математического ожидания. 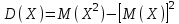 (8.8) (8.8)Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения. 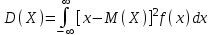 (8.9) (8.9)По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула: 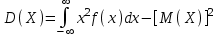 Свойства дисперсии 1) Дисперсия постоянной величины равна нулю. 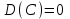 2) Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат.  3) Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин. 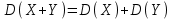 4) Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин. 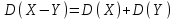 Теорема 8.4. Дисперсия числа появления события А в п независимых испытаниях, в каждом из которых вероятность р появления события постоянна, равна произведению числа испытаний на вероятности появления и не появления события в каждом испытании. 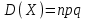 Определение. Средним квадратическим отклонением случайной величины Х называется квадратный корень из дисперсии. 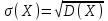 (8.10) (8.10)Наряду с дисперсии и среднеквадратическим отклонением мерой разброса (вариации) случайной величины относительно своего центра является относительное стандартное отклонение, или коэффициент вариации. Определение. Относительное стандартное отклонение, или коэффициент вариации определяет разброс значений случайной величины на единицу математического ожидания, определяется путем деления среднеквадратического отклонения случайной величины на ее математическое ожидание: 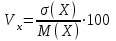 . (8.11) . (8.11)Если величина коэффициента вариации менее 33%, то совокупность однородна. Определение. Модой М0 дискретной случайной величины называется ее наиболее вероятностное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой функция плотности распределения достигает максимума. 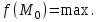 Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным. Если распределение имеет минимум, но не имеет максимума, то оно называется антимодальным. Определение. Медианой MD случайной величины Х называется такое ее значение, относительно которого справедливо равенство 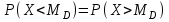 (8.12) (8.12)Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам. Определение. Начальным моментом порядка kслучайной величины Х называется математическое ожидание величины Хk. 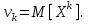 Для дискретной случайной величины: 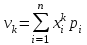 . .Для непрерывной случайной величины:  . .Начальный момент первого порядка равен математическому ожиданию. 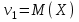 . .Определение. Центральным моментом порядка k случайной величины Х называют математическое ожидание случайной величины 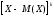 : :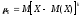 . .Для дискретной случайной величины: 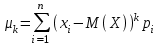 . .Для непрерывной случайной величины: 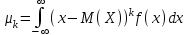 . .Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. 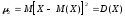 . .Центральный момент третьего порядка характеризует асимметрию распределения. Для вычисления центральных моментов используют формулы: 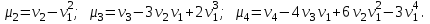 Определение. Отношение центрального момента третьего порядка к среднему квадратическому отклонению в третьей степени называется коэффициентом асимметрии. 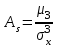 (8.13) (8.13)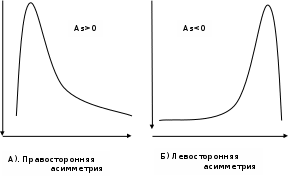 Рисунок 8.5. Асимметрия кривой распределения Для характеристики островершинности или плосковершинности распределения используется величина, называемая эксцессом. Определение. Эксцессом называется величина равная 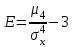 . (8.14) . (8.14)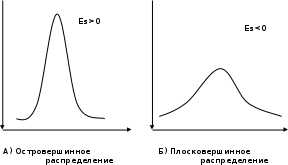 Рисунок 8.6. Эксцесс кривой распеределения. 8.4. Основные законы распределения Биноминальное распределение Если производится п независимых испытаний, в каждом из которых событие А может появиться с одинаковой вероятностью р в каждом из испытаний, то вероятность того, что событие не появится, равна q = 1 – p. Примем число появлений события в каждом из испытаний за некоторую случайную величину Х. Определение. Дискретная случайная величина Х, которая может принимать только целые неотрицательные значения 0,1,2,3, …,п с вероятностью 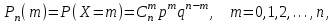 (8.15) (8.15)p+q=1, p>0, q>0 называется распределенной по биномиальному закону, где р- параметром биномиального распределения. Ряд распределения случайной величины представляется в виде
Функция распределения в этом случае определена формулой  . .Числовые характеристики биномиального распределения. 1. Математическое ожидание случайной величины: 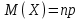 . .2. Дисперсия случайной величины 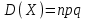 . .3. Среднее квадратическое отклонение  . .Распределение Пуассона. (Симеон Дени Пуассон (1781 – 1840) – французский математик) Определение. Дискретная случайная величина Х, которая может принимать только целые неотрицательные значения 0,1,2,3, …,т, …(бесконечное, но счетное множество значений) с вероятностью 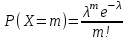 , где , где (8.16) (8.16)называется распределенной по закону Пуассона, где - параметр распределения. Ряд распределения случайной величины представляется в виде
Числовые характеристики распределения Пуассона. 1. Математическое ожидание случайной величины: 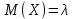 . .2. Дисперсия случайной величины 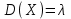 . .3. Среднее квадратическое отклонение 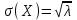 . .Если число испытаний п достаточно велико, а вероятность появления события в каждом испытании мала (p0,1), при условии, что 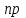 постоянная величина, то закон распределения Пуассона является приближением биномиального распределения. постоянная величина, то закон распределения Пуассона является приближением биномиального распределения. (Студентам предлагается самостоятельно рассмотреть геометрическое распределение и гипергеометрическое распределение) Нормальный закон распределения Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности 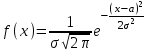 (8.16) (8.16)Нормальный закон распределения также называется законом Гаусса. Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения. Можно легко показать, что параметры a и  , входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х , входящие в плотность распределения являются соответственно математическим ожиданием и средним квадратическим отклонением случайной величины Х 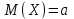 , σ(Х)= , σ(Х)= , дисперсия равна D(X)= , дисперсия равна D(X)= , коэффициент асимметрии , коэффициент асимметрии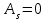 , эксцесс равен , эксцесс равен  . .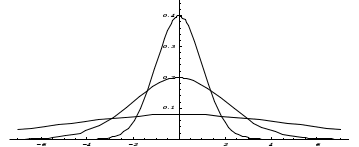 Рисунок 8.7. График функции плотности распределения. Построены графики (рис.8.7) при a =0 и трех возможных значениях среднего квадратичного отклонения = 1, = 2 и = 7. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается. Если а> 0, то график сместится в положительном направлении, если а< 0 – в отрицательном. При а = 0 и = 1 кривая называется нормированной. Уравнение нормированной кривой: 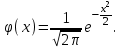 Функция распределения нормального закона F(x) имеет вид 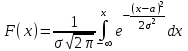 Функция распределения нормированного нормального закона F(x) имеет вид 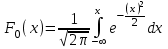 Интеграл относится к классу не берущихся интегралов в элементарных функциях, поэтому для нахождения функции распределения случайной величины, вероятности ее попадания на некоторый промежуток используют функцию Лапласа (интегралом вероятностей) 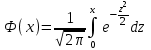 . .Найдем вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.  Обозначим 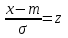 . . Тогда 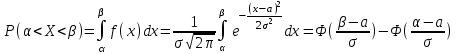 / /Вероятность попадания случайной величины в интервал (0;х) можно найти, используя функцию Лапласа (интеграл вероятностей) 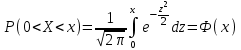 . Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах. . Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.Учитывая свойства, описанные ранее (студентам рекомендуется определить эти свойства) 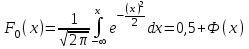 Функция Лапласа обладает следующими свойствами: 1) Ф(0) = 0; 2) Ф(-х) = - Ф(х); 3) Ф() = 0,5. Ниже показан график нормированной функции Лапласа. 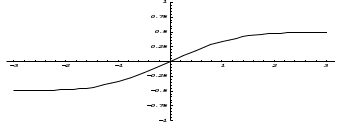 Рисунок 8.8. График нормированной функции Лапласа При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм. Рассмотрим вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины : 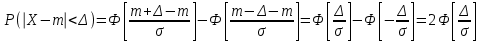 Если принять = 3, то получаем с использованием таблиц значений функции Лапласа:  Правило трех сигм Если случайная величина Х имеет нормальный закон распределения с параметрами а и  , то вероятность того что ее значения заключены в интервале , то вероятность того что ее значения заключены в интервале 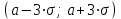 равна 0,9973. равна 0,9973.Т.е. вероятность того, что случайная величина отклонится по абсолютной величине от своего математического ожидание на величину, большую чем утроенное среднее квадратичное отклонение, практически равна нулю. Не практике считается, что если для какой – либо случайной величины выполняется правило трех сигм, то эта случайная величина имеет нормальное распределение. |