Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
|
Государственное казенное образовательное учреждение высшего образования «Российская таможенная академия» Ростовский филиал Н.В. Ширкунова, М.М. Цвиль, Г.О. Вафодорова МАТЕМАТИКА В ЭКОНОМИКЕ Учебное пособие Ростов-на-Дону 2019 Государственное казенное образовательное учреждение высшего образования «Российская таможенная академия» Ростовский филиал Н.В. Ширкунова, М.М. Цвиль, Г.О. Вафодорова МАТЕМАТИКА В ЭКОНОМИКЕ Учебное пособие Ростов-на-Дону 2019 Допущено Учебно-методическим советом Российской таможенной академии в качестве учебного пособия для обучающихся по направлению подготовки 38.05.02 Таможенное дело Рецензенты: И.В. Добрынина доктор физ.-мат. наук, профессор кафедры высшей математики АГЗ МЧС России ; Г.Ю. Рябых, профессор кафедры прикладной математики ДГТУ, канд. физ.-мат.наук, доцент Ширкунова Нина Васильевна, зав.кафедрой таможенной статистики РТА , канд. экон. наук, доцент, Цвиль Мария Михайловна, доцент кафедры информатики и информационных таможенных технологий Ростовского филиала РТА канд. физ.-мат. наук, доцент, Вафодорова Гулпари Одинаевна доцент кафедры таможенной статистики РТА канд. физ.-мат. наук Ширкунова Н.В., Цвиль М. М., Вафодорова Г.О. Математика в экономике: учебное пособие/ Н.В. Ширкунова, М.М. Цвиль, Г.О. Вафодорова – Ростов н/Д: Российская таможенная академия, Ростовкий филиал, 2019. В учебном пособии изложены теоретические основы дисциплины «Математика в экономике» необходимые студентам Академии для успешного освоения дисциплины. Рассмотрены основные положения матричного анализа, систем линейных уравнений, линейного программирования, теории вероятностей и математической статистики. Материал каждого раздела проиллюстрирован примерами. Учебное пособие рассчитан на студентов Российской таможенной академии специальности «Таможенное дело», а также рекомендуется в качестве дополнительной литературы студентам, обучающимся по направлению подготовки «Менеджмент», «Экономика» © Российская таможенная академия, 2019  СОДЕРЖАНИЕ Предисловие РАЗДЕЛ 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ Глава 1. Матрицы и определители Глава 2. Решение систем линейных уравнений Глава 3. Модель Леонтьева многоотраслевой экономики Контрольные вопросы к разделу 1 Тестовые задания для самопроверки к разделу 1 РАЗДЕЛ 2. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ Глава 4. Общая задача линейного программирования. Методы решения задач линейного программирования: графические и аналитические Глава 5. Транспортная задача линейного программирования и ее решение. Двойственные задачи линейного программирования Контрольные вопросы к разделу 2 Тестовые задания для самопроверки к разделу 2 РАЗДЕЛ 3. ЭЛЕМЕНТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ Глава 6. Основные понятия теории вероятностей. Случайные события Глава 7. Основные теоремы теории вероятностей Глава 8. Случайные величины Глава 9. Основные понятия математической статистики. Статистические оценки параметров распределения Основные элементы сетевого планирования Глава 10. Проверка статистических гипотез Глава 11.Корреляция и регрессия Контрольные вопросы к разделу 3 Тестовые задания для самопроверки к разделу 3 Заключение Библиографический список ПРЕДИСЛОВИЕСовременная экономическая наука предполагает широкое использование математики. Математика являются основой для разработки методов и моделей любой экономической науки, включая и экономическую теорию. Использование аппарата математики позволяет проводить глубокий анализ функционирования экономических систем. Целью подготовки данного пособия является формирование у студентов способности использовать основы математических знаний при оценке эффективности результатов деятельности в различных сферах и анализировать тенденции развития российской и мировой экономик. Учебное пособие разработано в соответствии с требованиями ФГОС ВО и рабочей программой дисциплины «Математика в экономике» по специальности «Таможенное дело». При подготовке учебного пособия авторы руководствовались принципом повышение уровня фундаментальной математической подготовки студентов. В каждой главе учебного пособия приводится теоретический материал (основные определения, свойства, теоремы и соответствующие формулы), и рассматривается решение типовых задач. Все разделы содержат тестовые задания и контрольные вопросы. Учебное пособие позволит студентам успешно освоить дисциплину «Математика в экономике». Авторы учебного пособия Нина Васильевна Ширкунова, зав.кафедрой таможенной статистики РТА, канд. экон. наук, доцент– раздел 1 глава 3, раздел 3. Мария Михайловна Цвиль, доцент кафедры информатики и информационных таможенных технологий Ростовского филиала РТА, канд. физ.-мат. наук, доцент – раздел 2. Гулпари Одинаевна Вафодорова доцент кафедры таможенной статистики РТА канд. физ.-мат. наук – раздел 1 глава1,2. РАЗДЕЛ 1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ Глава 1. Матрицы и определители 1.1. Виды матриц Определение.Матрицей c размерами mxnназывается прямоугольная таблица чисел, содержащая m строк и nстолбцов. Числа, составляющие матрицу, называются элементами матрицы. Матрицы обычно обозначаются прописными буквами латинского алфавита, например A, B, C,…, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: aij , i - номер строки, j- номер столбца. Индексы i и j определяют расположение элемента aij в матрице A и играют роль координат этого элемента в прямоугольной таблице чисел. Например, матрица 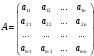 имеет mстрок, nстолбцов. Матрица, состоящая из одной строки, 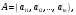 называется матрицей - строкой, или вектором. называется матрицей - строкой, или вектором.Матрица, состоящая из одного столбца 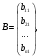 называется матрицей столбцом, или вектором называется матрицей столбцом, или вектором Определение. Если в матрице А размера 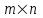 число строк равно числу столбцов (т.е. m = n), то матрица A называется квадратной матрицей n-го порядка, а число n–порядком матрицы A. число строк равно числу столбцов (т.е. m = n), то матрица A называется квадратной матрицей n-го порядка, а число n–порядком матрицы A. Определение. Если в матрице А размера 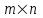 число строк не равно числу столбцов (т.е. m ≠n), то матрица A называется прямоугольной матрицей число строк не равно числу столбцов (т.е. m ≠n), то матрица A называется прямоугольной матрицей 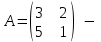 квадратная матрица второго порядка, квадратная матрица второго порядка,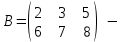 прямоугольная матица размера прямоугольная матица размера 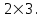 Определение. Матрица 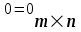 называется нулевой матрицей размера называется нулевой матрицей размера 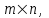 если все ее элементы равны нулю, т.е если все ее элементы равны нулю, т.е 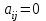 ( i=1,2,3,…,m; j=1,2,…,n). ( i=1,2,3,…,m; j=1,2,…,n).Элементы квадратной матрицы 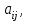 у которых номер строки совпадает с номером столбца, называются диагональнымии образуют главную диагональ. Квадратная матрица E называется единичной, если по главной диагонали стоят единицы, остальные элементы равны нулю. у которых номер строки совпадает с номером столбца, называются диагональнымии образуют главную диагональ. Квадратная матрица E называется единичной, если по главной диагонали стоят единицы, остальные элементы равны нулю. Определение. Если диагональные элементы матрицы не равны нулю, а все элементы, стоящие ниже главной диагонали, равны нулю, то матрица называется трапециевидной или ступенчатой. 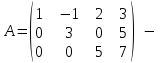 трапециевидная (ступенчатая) матрица размера трапециевидная (ступенчатая) матрица размера 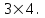 Произвольная матрица вида 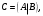 составленная из двух матриц, разделенных вертикальной чертой, называется расширенной. составленная из двух матриц, разделенных вертикальной чертой, называется расширенной. Например, матрица 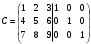 является расширенной. Она составлена из квадратной матрицы третьего порядка и единичной матрицы третьего порядка. 1.2. Операции над матрицами Определение. Суммой матриц A и B размера 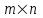 называется матрица C=A+B того же размера такая, что называется матрица C=A+B того же размера такая, что 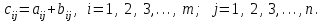 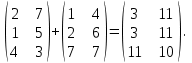 Определение. Произведением матрицы A размера 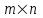 на число на число 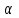 называется матрица называется матрица 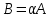 того же размера такая, что того же размера такая, что 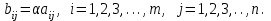 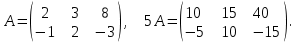 Из определения произведения матрицы на число следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы.  Определение. Разностьюматриц B и A называется матрица X такая, что A+X=B. Разность матриц B и A всегда одна, находится по формуле X=B+(-1)A и обозначается B-A. Операции сложения матриц и умножения матриц на число обладают следующими свойствами: 1. A+B=B+A 2. (A+B)+C=A+(B+C) 3.  4.  5.  6. 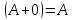 (0- нулевая матрица). (0- нулевая матрица).7. 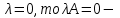 нулевая матрица нулевая матрицаЗдесь A, B, C, 0 – матрицы одного типа, 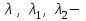 числа. числа.Операция умножения матрицы А на матрицу B определена, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц 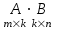 называется такая матрица называется такая матрица 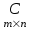 , каждый элемент , каждый элемент 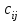 которой равен сумме произведений элементов которой равен сумме произведений элементов 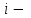 й строки матрицы A на соответствующие элементы й строки матрицы A на соответствующие элементы 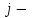 го столбца матрицы B: го столбца матрицы B: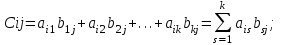 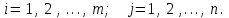 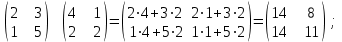 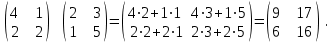 Определение. Если AB=BA, то матрицы A и B называются перестановочнымиили коммутирующими. Особую роль при умножении матриц играет единичная матрица E, она по своим свойствам очень похожа на обычную числовую единицу. Легко проверить, что при умножении любой прямоугольной матрицы A размера 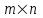 на единичную матрицу Em слева и на единичную матрицу En на единичную матрицу Em слева и на единичную матрицу En справа, матрица A не меняется, т.е. справа, матрица A не меняется, т.е.EmA=AEn= A. Кроме того, очевидно, что 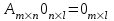 и и 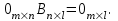 Интересно, однако, что из равенства AB=0 не следует, что A=0 или B=0. 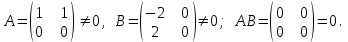 Умножение матриц обладает следующими свойствами: 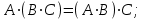 2) 2) 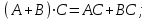 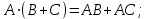 4) 4) 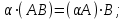 Транспонирование матрицы Определение. Пусть A – матрица 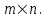 Матица Матица 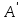 или или 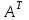 размера размера 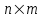  называется транспонированной к A, если называется транспонированной к A, если 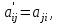 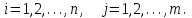 Очевидно, что матрица 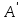 получается поворотом вокруг главной диагонали матрицы A. При этом повороте i-й столбец матрицы A преобразуется в i-ю строку матрицы получается поворотом вокруг главной диагонали матрицы A. При этом повороте i-й столбец матрицы A преобразуется в i-ю строку матрицы 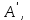 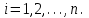  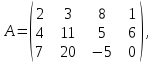 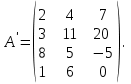 Если A-вектор- строка, то 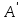 -вектор-столбец. -вектор-столбец.A=(1 2 3 4 5), 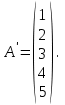 Операция транспонирования обладает следующими свойствами: 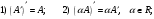 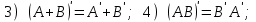 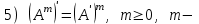 целое. целое. Возведение в степень. Целой положительной степенью 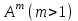 квадратной матрицы A называется произведение квадратной матрицы A называется произведение 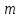 матриц, равных A, т.е. матриц, равных A, т.е.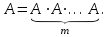 Заметим, что операция возведения в степень определяется только для квадратных матриц. По определению полагают 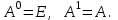 Нетрудно показать, что Нетрудно показать, что 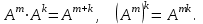 Пример 1. Найти 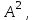 где где 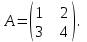 Решение. 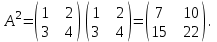 1.3 Понятие определителя квадратной матрицы. Свойства определителей. Вычисление определителей. Любой квадратной матрице A по определенному правилу можно сопоставить некоторое число, которое называется определителем (детерминантом) матрицы A и обозначается det (A) или  . Если A – матрица n-го порядка . Если A – матрица n-го порядка 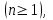 то вместо слов определитель матрицы A часто говорят определитель n-го порядка. то вместо слов определитель матрицы A часто говорят определитель n-го порядка. Определитель  матрицы 1-го порядка матрицы 1-го порядка 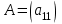 есть элемент матрицы 1-го порядка: есть элемент матрицы 1-го порядка: 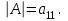 Определитель  матрицы 2-го порядка матрицы 2-го порядка 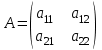 есть число есть число 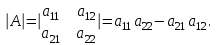 Определителем матрицы 3-го порядка  называется число называется число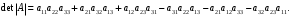 Минором 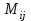 элемента aijматрицы An–го порядка называется определитель (n-1)-го порядка, полученный из матрицы A вычеркиванием i-й строки и j-го столбца. Например, минор элемента a23 матрицы третьего порядка получается вычеркиванием из матрицы второй строки и третьего столбца. элемента aijматрицы An–го порядка называется определитель (n-1)-го порядка, полученный из матрицы A вычеркиванием i-й строки и j-го столбца. Например, минор элемента a23 матрицы третьего порядка получается вычеркиванием из матрицы второй строки и третьего столбца.Алгебраическим дополнением Aij элемента aij матрицы A n-го порядка называется минор 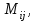 взятый со знаком (-1)1+j. взятый со знаком (-1)1+j.Пример 2. Вычислить определитель 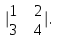 Решение. 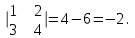 Пример 3. Вычислить определитель 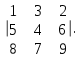 Решение. 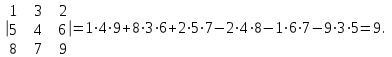 Определители матриц n- го порядка ( 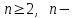 целое) целое)Определение. Строка S=(s1 s2 … sn) называется перестановкойчисел 1, 2, …, n, если все элементы строки S попарно различны и для любого k, (k=1, 2, …, n) sk равно одному из чисел 1, 2, …, n. Коротка говоря, строка S получается из строки (1 2 3… n) перестановкой элементов. Из комбинаторики известно, что число всех таких перестановок чисел 1, 2, …, n, равно n!=1∙2∙3∙…∙n. Определение. Говорят, что элементы 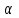 и и 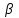 в перестановке S образуют инверсию(беспорядок), если в перестановке S образуют инверсию(беспорядок), если 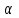 стоит левее стоит левее 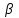 и и 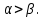 Число всех инверсий в перестановке S обозначается k(S). Число всех инверсий в перестановке S обозначается k(S).Определение. Пусть дана матрица n-го порядка 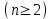 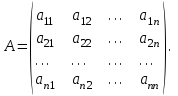 Введем число det (A), которое вычисляется по правилу: 1) найдем все n! перестановок чисел 1, 2, 3,…, n; 2) для каждой перестановки S=(s1 s2 … sn) составим произведение 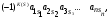 где k(S)- число инверсий перестановки S; где k(S)- число инверсий перестановки S;3) сложим все n! произведений из предыдущего пункта и получим число det (A). Число det(A) называется определителем матрицы A. Свойства определителей 1) Если все элементы какой – либо строки или столбца равны нулю, то определитель равен нулю. 2) Если элементы двух строк или столбцов равны или пропорциональны, то определитель равен нулю. 3) При транспонировании матрицы величина определителя не меняется. 4) Если к элементам одной строки прибавить умноженные на одно и то же не равное нулю число элементы другой строки, величина определителя не изменится. 5) При перестановке строк или столбцов местами определитель меняет знак. 6) Если элементы какой – либо строки или столбца умножить на одно и то же число, то определитель умножится на это число. Разложение определителя по строке или столбцу Верны следующие формулы, которые позволяют свести вычисление определителя n-го порядка к вычислению определителей порядка n-1: 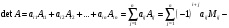 разложение определителя по i-й строке. разложение определителя по i-й строке. Каждый элемент i-й строки aij умножается на свое алгебраическое дополнение Aij(вычеркиваются i-я строка и j-й столбец, то есть строка и столбец, содержащие элемент aij, вычисляется определитель полученной матрицы и умножается на (-1)i+j ), полученные произведения суммируются. 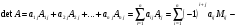 разложения определителя поj-му столбцу. Каждый элементj-го столбца aijумножается на свое алгебраическое дополнение Aij (вычеркиваются i- я строка и j–й столбец, то есть строка и столбец, содержащие элемента aij , вычисляется определитель полученной матрицы и умножается на (-1)i+j),полученные произведения суммируются. разложения определителя поj-му столбцу. Каждый элементj-го столбца aijумножается на свое алгебраическое дополнение Aij (вычеркиваются i- я строка и j–й столбец, то есть строка и столбец, содержащие элемента aij , вычисляется определитель полученной матрицы и умножается на (-1)i+j),полученные произведения суммируются.Пример 4. Разложим определитель по 1-й строке. 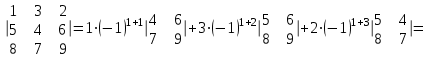 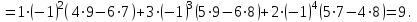 Разложим определитель по 1-му столбцу. 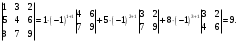 Независимо от способа разложения всегда получается один и тот же ответ. Вычисление определителей Выбирается строка (или столбец) определителя, содержащая больше всего нулей. Используя свойство (4), зануляют в этой строке (или столбце) все элементы, кроме одного. После чего разлагают определитель по строке (или столбцу). К полученному определителю применяют эту же схему. Вычислить определитель пятого порядка 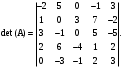 Прибавляя ко второй строке утроенную пятую и вычитая из четвертой строки учетверенную пятую, получим: 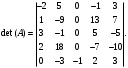 Разложив этот определитель по третьему столбцу, содержащему лишь один не равный нулю элемент (с суммой индексов 5+3, т.е. четной), получим 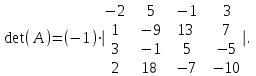 Преобразуем вновь полученный определитель, прибавляя к первой строке удвоенную вторую и вычитая из третьей строки утроенную вторую, а из четвертой – удвоенную вторую: 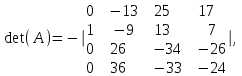 а затем разложим его по первому столбцу, причем заметим, что единственному не равному нулю элементу этого столбца соответствует нечетная сумма индексов, получим: 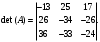 Вычислим этот определитель третьего порядка, предварительно разложив его по третьей строке: 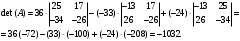 С теоретической точки зрения при вычислении определителя безразлично, какую строку или столбец взять для разложения. С практической точки зрения лучше брать линию, которая содержит нулевые элементы, и чем их больше, тем лучше. 1.4. Понятие обратной матрицы. Теорема о существовании обратной матрицы. Свойства обратных матриц. Пусть A – квадратная матрица n-го порядка, 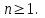 Определение. Матрица A-1 называется обратной к квадратной матрице A, если выполняется равенство 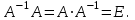 Если det(A) ≠ 0, то квадратная матрица A называется невырожденной или неособенной. Если det (A) = 0, то квадратная матрица A называется вырожденной или особенной. Теорема 1.1. (о существовании обратной матрицы). Обратная матрица A-1 существует и единственна тогда и только тогда, когда исходная матрица невырожденна. Алгоритм вычисления обратной матрицы. 1 Находим определитель исходной матрицы. Если 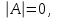 то матрица A вырожденная и обратной матрицы A-1 не существует. Если то матрица A вырожденная и обратной матрицы A-1 не существует. Если 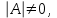 то матрица A невырожденная и обратная матрица существует. то матрица A невырожденная и обратная матрица существует.2. Находим матрицу 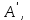 транспонированную к A. транспонированную к A.3. Находим алгебраические дополнения элементов транспонированной матрицы 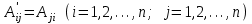 и составляем из них присоединенную матрицу и составляем из них присоединенную матрицу 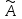 : : 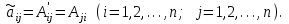 4. Вычисляем обратную матрицу по формуле 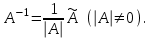 5. Проверяем правильность вычисления обратной матрицы A-1 , исходя из ее определения: 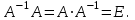 Свойства обратных матриц 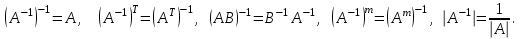 Пример 5. Для матрицы 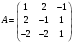 найти обратную A-1 . найти обратную A-1 .Решение. 1 Способ- метод присоединенной матрицы. Обратную матрицу будем искать, делая следующие шаги: находим определитель матрицы A. Его величина 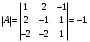 Следовательно, обратная матрица существует. находим транспонированную к A матрицу 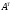 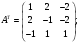 находим алгебраические дополнения к элементам матрицы 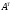 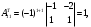 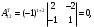 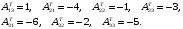 Выписываем присоединенную матрицу: 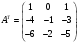 вычисляем обратную матрицу: 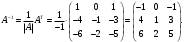 Другой способ вычисления обратной матрицы дает метод Жордана. 2 способ метод Гаусса-Жордана. Составим расширенную матрицу из исходной и единичной. Посредством элементарных преобразований преобразуем расширенную матрицу так, чтобы исходная матрица превратилась в единичную. Тогда на месте единичной матрицы образуется обратная. Делаем следующие элементарные преобразования: 1) складываем элементы 1-й строки с элементами 3-й и размещаем на месте 3-й строки; 2) умножаем 2-ю строку на 2 и складываем с 3-й, предварительно умноженной на 3, результат размещаем на месте 3-й строки, левая часть матрицы стала треугольной; 3) образуем треугольник нулей выше главной диагонали, для чего умножаем 3-ю строку на -3 и складываем со 2-й, результат размещаем на месте 2-й строки; 4) умножаем 3-ю строку на 2 и складываем с 1-й, результат размещаем на месте 1-й строки; 5) складываем 2-ю строку с 1-й и размещаем на месте 1-й строки; 6) умножаем 3-ю строку на -1, 2-ю строку на -0,5. Таким образом, слева удалось получить единичную матрицу, но тогда справа образовалась обратная. 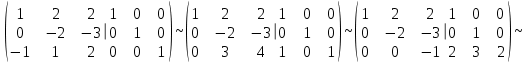 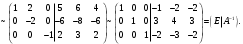 Видно, что 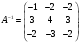 1.5. Определение ранга матрицы. Теорема о ранге матрицы при элементарных преобразованиях. Определение. Рангом матрицы называется наивысший порядок отличных от нуля миноров этой матрицы. Ранг матрицы A обозначается rang A, или r(A). Свойства ранга: Ранг нулевой матрицы считается равным нулю. rang A ≤ min(m,n). r (A) =n у матрицы n- го порядка тогда и только тогда, когда |A|≠0. Теорема 1.2. (о ранге матрицы при элементарных преобразованиях) Элементарные преобразования не изменяют ранг матрицы: изменение порядка строк или столбцов; умножение элементов одной строки или столбца на любое не равное нулю число; сложение строк с предварительным умножением любой из них на произвольное не равное нулю число; отбрасывание нулевой строки или столбца; транспонирование. Метод 1. Нахождения ранга матрицы по определению. Этот метод требует, как правило, вычисления большого количества миноров, что приводит к значительным трудностям. Пример 6 . Вычислить ранг матрицы 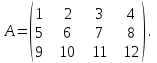 Решение. Эта матрица прямоугольная ( m=3, n=4). Наивысший порядок определителей, входящих в матрицу, равен трем. Эти определители могут быть получены только вычеркиванием одного столбца (m 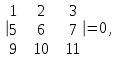 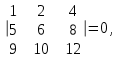 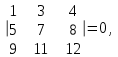 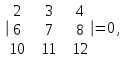 Все определители третьего порядка равны нулю, поэтому rangA ≤ 2.Переходим к рассмотрению определителей второго порядка. Вычеркнем, например, 3-ю строку и 3-й и 4-й столбцы. Тогда имеем определитель: 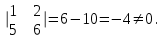 Следовательно, высший порядок отличных от нуля определителей, входящих в матрицу, есть 2, а поэтому rang A=2. Метод 2. Метод элементарных преобразований. Элементарные преобразования не меняют ранга матрицы. Применяя элементарные преобразования, можно привести матрицу к такому виду, когда все элементы, кроме 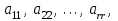 равны нулю. Число отличных от нуля элементов преобразованной матрицы, очевидно, равно рангу матрицы. равны нулю. Число отличных от нуля элементов преобразованной матрицы, очевидно, равно рангу матрицы.Пример 7. Найти ранг матрицы 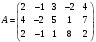 Решение: Ко второй строке прибавим первую, предварительно умноженную на -2, к третьей строке прибавим первую, предварительно умноженную на -1. Получим 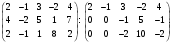 К третьей строке прибавим вторую, предварительно умноженную на -2: 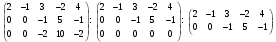 Числено ненулевых строк равно 2. Тогда rang A=2. При ином обосновании выделим из матриц минор максимального порядка, не равны нулю. Это, например, 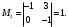 Тогда rang A=2. Тогда rang A=2. |
