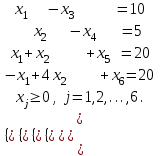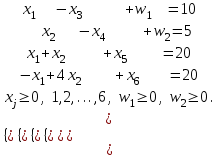Курсовая. Матем-ка в эк-ке Цвиль М.М (1). Математика в экономике
 Скачать 2.11 Mb. Скачать 2.11 Mb.
|
4.5. Метод искусственного базисаМетод искусственного базиса применяется для решения задач ЛП в случае, когда задача не имеет начального опорного решения с базисом из единичных векторов [3]. Пусть задана задача ЛП в канонической форме, то есть имеет вид (4.7) – (4.8), и в ней отсутствует единичный базис. К этой задаче строим вспомогательную задачу (ВЗ): 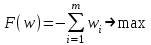 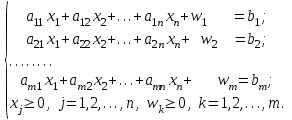 Здесь w1, w2,…, wm – искусственные переменные. Запишем ограничения в векторном виде: A1x1+A2x2+…+Anxn+An+1w1+…+An+mwm =B, где  , , 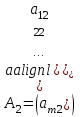 , …, , …, 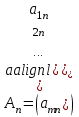 , , 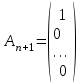 , , 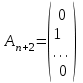 , …, , …, 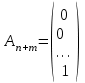 , , 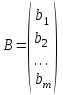 . Таким образом, вектора . Таким образом, вектора 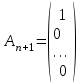 , , 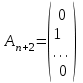 , …, , …, 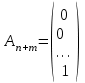 образуют единичный базис в Rm, и все искусственные переменные соответствующие этим векторам будут базисными. Далее строится обычная симплекс-таблица. Если ВЗ не имеет решения в силу неограниченности целевой функции, то исходная задача также не имеет решения по той же причине. Пусть в результате знакомых по симплекс-методу необходимых преобразований получили оптимальную симплекс-таблицу к ВЗ. Очевидно, что максимальное значение целевой функции ВЗ равно 0, то есть maxF=0. Если же maxF<0, то исходная задача ЛП не имеет решения в силу несовместности системы ограничений. Предположим, что maxF=0. Тогда возможны такие ситуации: образуют единичный базис в Rm, и все искусственные переменные соответствующие этим векторам будут базисными. Далее строится обычная симплекс-таблица. Если ВЗ не имеет решения в силу неограниченности целевой функции, то исходная задача также не имеет решения по той же причине. Пусть в результате знакомых по симплекс-методу необходимых преобразований получили оптимальную симплекс-таблицу к ВЗ. Очевидно, что максимальное значение целевой функции ВЗ равно 0, то есть maxF=0. Если же maxF<0, то исходная задача ЛП не имеет решения в силу несовместности системы ограничений. Предположим, что maxF=0. Тогда возможны такие ситуации:1) все искусственные переменные стали свободными и были исключены из таблицы. В этом случае вычеркиваем столбцы, соответствующие искусственным переменным и последнюю строку. Вместо неё приписываем новую строку оценок, но с использованием исходной целевой функции Z(X). Тем самым получена начальная симплекс-таблица для исходной задачи ЛП, к которой применяем симплекс-метод; 2) в оптимальном решении ВЗ хотя бы одна искусственная переменная осталась базисной. Тогда: а) либо все числа в строках, соответствующих оставшимся базисным искусственным переменным, равны 0; б) либо есть хоть одно отличное от 0. В первом случае, поступаем также как и пункте 1). Во втором, выбираем любой ненулевой элемент в качестве ведущего и делаем шаг жордановых исключений. Через конечное число шагов мы придем или к пункту 1), или к пункту 2а). Заметим, что если среди векторов Aj , j=1,2,…,n, были вектора, которые могли бы войти в базис, то искусственные переменные вводят только в те уравнения системы ограничений, в которых отсутствует базисная переменная. Пример 4. Минимизировать функцию 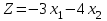 при ограничениях при ограничениях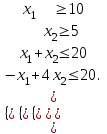 Решение: Если ввести дополнительные неотрицательные переменные 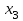 , , 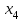 , , 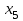 , , 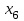 , и перейти к задаче на нахождение максимума целевой функции, то исходная задача примет вид: , и перейти к задаче на нахождение максимума целевой функции, то исходная задача примет вид:Z1= 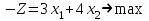
По виду ограничений (4.14) следует, что очевидного базисного допустимого решения нет. Для порождения базисного допустимого решения применим метод искусственного базиса. Изменим первые два ограничения (два других не создают проблем) введением в левую часть искусственных переменных w1 и w2 (w1,w2 0). Решаем ВЗ: F=-w1-w2max
Базисное решение (допустимый план) будет иметь вид: 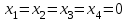 , а , а 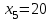 , , 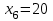 , w1=10, w2=5. Строим симплекс-таблицу к ВЗ, соответствующую начальному опорному плану: , w1=10, w2=5. Строим симплекс-таблицу к ВЗ, соответствующую начальному опорному плану:
Проводя преобразования по методу Жордана-Гаусса, на втором шаге будем иметь оптимальную симплекс-таблицу для ВЗ (4.15). Вычеркивая столбцы, соответствующие искусственным переменным и последнюю строку, и приписывая новую строку оценок с использованием целевой функции Z1(X), получим начальную симплекс-таблицу для задачи :
Преобразования по методу Жордана-Гаусса с последней таблицей приведены ниже:
Все оценки стали положительными, и, следовательно, 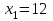 , , 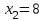 , , 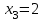 , , 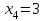 , x5=x6=0. Так как , x5=x6=0. Так как 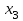 и и 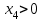 , то ограничения, в которые эти переменные входят, превращаются в строгие неравенства. При этом, Z1max=Z1(12;8;2;3;0;0)=68, а Zmin= -Z1max=-68. , то ограничения, в которые эти переменные входят, превращаются в строгие неравенства. При этом, Z1max=Z1(12;8;2;3;0;0)=68, а Zmin= -Z1max=-68.4.6. Решение оптимизационных задач с помощью надстройки «Поиск решения» в среде Excel. Поиск решения – это надстройка Excel, которая позволяет решать оптимизационные задачи. После выбора команды Поиск решения появится диалоговое окно Параметры поиска решения, в котором есть три основных поля: 1) оптимизировать целевую функцию; 2) изменяя ячейки переменных; 3) в соответствии с ограничениями. Сначала нужно заполнить поле − Оптимизировать целевую Функцию. Целевая ячейка должна содержать формулу. Можно выбрать поиск наименьшего или наибольшего значения для целевой ячейки или установить конкретное значение. В поле − Изменяя ячейки переменных следует ввести имена для каждого диапазона ячеек переменных или ссылки на них. В поле в соответствии с ограничениями вводятся любые необходимые ограничения. Пример 5. Найдем решение задачи о производстве изделий двух видов (см. пример1), используя «Поиск решения» в среде Excel: 1. Заполним рабочий лист MS Excel согласно рис.4.2.  Рис. 4.2. Начальные данные 2. Перейдем к решению данной задачи. 2.1. Запустите инструмент "поиск решения" (Office – Параметры Excel – Надстройки – в раскрывающемся списке Управление – Надстройки Excel – Перейти – установить флажок Поиск решения). Далее вкладка Данные, панель Анализ. Выполним команду Поиск решения. В появившемся диалоговом окне заполним поля согласно рис. 4.3. При добавлении ограничений воспользуемся кнопкой Добавить. 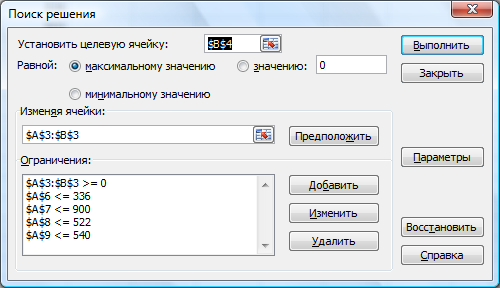 Рис. 4.3. Окно Поиск решения 2.2. После занесения данных нажать на кнопку Выполнить. 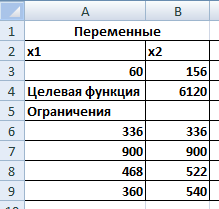 Рис. 4.4. Найденное решение Если все сделано правильно, Excel сообщит о том, что решение найдено и удовлетворяет ограничениям (см. рис.4.4). Оптимальный план производства, дающий максимальную прибыль составляет 60 число изделий первого вида и 156 число изделий второго вида. Этот объем производства принесет 6120 тыс. руб. прибыли. Глава 5. Двойственные задачи линейного программирования. Транспортная задача линейного программирования и ее решение. |