Методы интерполяции и аппроксимации
 Скачать 93.46 Kb. Скачать 93.46 Kb.
|
МЕТОДЫ ИНТЕРПОЛЯЦИИ И АППРОКСИМАЦИИИнтерполяция Интерполяция – способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений. Пусть в ходе эксперимента при изменении входной величины х(x0, x1, x2,..., xn) получены значения функции y=f(x) (y0,y1,y2 yn) (табл. 1). Таблица 1 Вид таблицы экспериментальных данных
Интерполяцию функций применяют в случае, когда требуется найти значение функции y(х) при значении аргумента xi, принадлежащего интервалу [x0, …, xn], но не совпадающего по значению ни с одним значением, приведенным в таблице 1. Данная задача, а именно интерполяция функций, часто встречается при ограниченности возможностей при проведении эксперимента. В частности из-за дороговизны и трудоемкости проведения эксперимента размер выборки (x0, x1, x2,..., xn) может быть достаточно мал. При этом во многих случаях аналитическое выражение функции y(x) не известно и получить его по таблице ее значений (табл. 1) в большинстве случаев невозможно. Поэтому вместо нее строят другую функцию, которая легко вычисляется и имеет ту же таблицу значений (совпадает с ней в точках x0, x1, x2,..., xn), что и f(x), т. е. где i= 0, 1, 2, … , n. Pn(x0)=f(x0)=y0; … (1) Pn(xi)=f(xi)=yi; Нахождение приближенной функции называется интерполяцией, а точки x0, x1, x2, …, xn– узлами интерполяции. Интерполирующую функцию ищут в виде полинома nстепени. Для каждого набора точек имеется только один интерполяционный многочлен, степени не больше n. Однозначно определенный многочлен может быть представлен в различных видах. Графически задача интерполирования заключается в том, чтобы построить такую интерполирующую функцию, которая бы проходила через все узлы интерполирования (рис. 1). 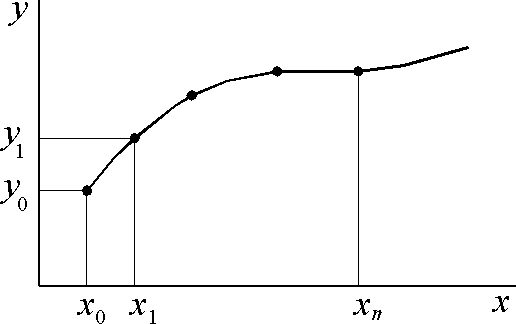 Рис. 1. Вид интерполирующей функции Рассмотрим канонический полином, линейную интерполяцию, интерполяционные многочлены Ньютона и Лагранжа. |
