Введение_в_математический_анализ. Методические указания к самостоятельной работе по дисципли не б. 1 Математика

• Название: Методические указания к самостоятельной работе по дисципли не б. 1 Математика
• Дата: 27.05.2022
• Размер: 168.01 Kb.
• Имя файла: Введение_в_математический_анализ.docx
• Тип: Методические указания; #552190
• страница: 3 из 27

Понятие сложной функции

Рассмотрим функцию y

lg x. Эта функция сконструи-

рована из двух простейших элементарных функций – логариф-

мической z=lg xи степенной

y , при этом аргумент zсте-

пенной функции

y принимает свои значения в области из-

менения логарифмической функции z=lg x. Таким образом,

функцию

y можно назвать функцией от функции. Такие

функции принято называть сложнымифункциями.

Как найти область определения сложной функции? Вер- немся к нашему примеру. Известно, что степенная функ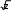ция

y определена для z 0 . Следовательно, сложная функция

y lg x

определена лишь для тех значений x, при которых

lg x 0 , то есть для x[1,) .

В общем случае, если функция z=g(x)определена на множестве X, а функция y=f(z)определена на множестве Z, то сложная функция у = f(g(х)) будет определена на множестве Хлишь тогда, когда множество значений функции g(x) будет вхо- дить в область определения функции f(z).

Сложную функцию y = f(g(x)) называют также наложением или суперпозицией функций z=g(x)и y=f(z).

Большинство функций, с которыми приходится иметь де- ло, являются сложными функциями. Например, функция

ysin x

является простейшей элементарной функцией, а функ-

ция

ysin 2x

– уже сложная функция. Она является комбинаци-

ей линейной функции z=2хи тригонометрической функции

ysin z. Сложная функция может быть суперпозицией трех и

большего числа функций. Например, функция

_{y 7}arctg

^xявляет-

ся наложением трёх простейших элементарных функций

u ,varctguи

y7^v. Так как функции

y7^v

и v arctg u

определены при любых значениях своих аргументов, то сложная

функция

_{y 7}arctg x

определена для всех x, при которых опреде-

лена функция u , то есть для x[0,) .

Понятие сложной функции позволяет значительно расши- рить множество элементарных функций. К элементарным функ- циям принято относить простейшие элементарные функции 1–7, а также все функции, которые получаются из простейших с по- мощью четырех арифметических действий и суперпозиций, по- следовательно применённых конечное число раз.

Пример. Найти область определения функции

yarcsin ^x ¹ .

3
Решение. Первое слагаемое функции

yarcsin ^x ¹

3

определено при условии, что слагаемое определено, когда

1 ^x1 3

или

3 x 3 . Второе

то есть при

x²+x+2>0  (x+2)(x–1)>0,

x(,2)(1,) . Найдем значения x, при кото-

рых определены оба слагаемых:

_{–3 –2} 1 3 x

Таким образом,

x[3,2)(1,3].