Введение_в_математический_анализ. Методические указания к самостоятельной работе по дисципли не б. 1 Математика
 Скачать 168.01 Kb. Скачать 168.01 Kb.
|
ПОНЯТИЕ ПРЕДЕЛА ФУНКЦИИВ связи с чем возникло понятие предела функции?Одной из основных задач математического анализа являет- ся изучение поведения функции в достаточно малой окрестно- сти некоторой точки x0 или при x . В связи с этим возникло понятие предела функции при x x0 и при x . В зависимо- сти от поведения функции y =f(x)геометрически возможны следующие ситуации (рис. 2.1–2.4).  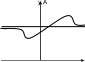 y yA 0 lim x x0 x f(x) A lim x 0 x f(x) A Рис. 2.1 Рис. 2.2   y yx lim x x0 f(x) lim x f(x) Рис. 2.3 Рис. 2.4 Определение предела функции в случаях 1–4def Определение 1. ( lim x x0 f(x) A) (ε 0 δ 0: 0 xx0 δ f(x) Aε) . Определение означает, что число A будет пределом функции y=f(x) при x x0 в том случае, если для x, попав- ших в достаточно малую проколотую (сама точка x0 не входит в окрестность, таким образом окрестность «проколота» в точке x0 ) окрестность точки x0 (0 x x0 δ) , соответствующие значе- ния f(x)попадут в сколь угодно малую окрестность числа A ( f(x) Aε) (рис. 2.1). Замечание. В определении предела не требуется, чтобы функция была определена в самой (∙)x0. Достаточно, чтобы функция была определена в проколотой окрестности (∙)x0. def Определение 2. (lim f(x) A) (ε 0 Δ 0: x x Δ f(x) A ε) . Определение означает, что для достаточно больших x x Δ соответствующие значения f(x)будут отличаться от A сколь угодно мало f(x) Aε ( рис. 2.2). def Определение 3. ( lim f(x)) (Ε 0 δ 0: x x0 0 xx0 δ f(x)) . Определение означает, что для x, попавших в достаточно малую проколотую окрестность (∙)x0 (0 xx0 δ) , соответст- вующие значения f(x) становятся сколь угодно большими ( f(x)) (рис. 2.3). def Определение 4. (lim f(x)) (Ε 0 Δ 0: x x Δ f(x) Ε) . |
