Введение_в_математический_анализ. Методические указания к самостоятельной работе по дисципли не б. 1 Математика

• Название: Методические указания к самостоятельной работе по дисципли не б. 1 Математика
• Дата: 27.05.2022
• Размер: 168.01 Kb.
• Имя файла: Введение_в_математический_анализ.docx
• Тип: Методические указания; #552190
• страница: 5 из 27

Определение односторонних пределов функции

В тех случаях, когда возникает необходимость в изучении поведения функции y = f(x) или только в левосторонней (x < x₀) или правосторонней (x > x₀) полуокрестностях точки x₀ , ис- пользуются так называемые односторонние пределы функции,

для которых приняты обозначения

lim

xx₀ 0

f(x)обозначение пре-

дела слева) и

lim

xx₀ 0

f(x)(обозначение предела справа).

def

( lim

x x₀ 0

f(x) A)  (ε  0 δ  0:

0  x₀  x δ

def

f(x) A ε) ;

( lim

x x₀ 0

f(x) A)  (ε  0 δ  0:

0  x x₀  δ

f(x) B ε) .

Из определения предела следует

^_ lim

f(x) A^_  ^_ lim

f(x)

lim f(x) A^_ .

_ x x<sub>0

 </sub> xx₀ 0

xx₀ 0 _

Пример 1. Изобразить схематично график функции

y=f(x), удовлетворяющей условиям:
D( y)(,2)(2,2 )(2,),

lim

x2

f(x),

lim f(x),

x2

lim f(x)0,

x

f(3 )0,

f(0 )0,

f(3 )0.

Решение.

lim

x2

f(x)  график функции

y f(x)

вблизи

точки x= -2 прижимается к прямой x= –2 , устремляясь вниз.

lim f(x) 

x2

график функции y=f(x)вблизи точки x

= 2 прижимается к прямой x= 2 , устремляясь вверх.

lim f(x)0 

x

мается к оси Ox.

график функции y=f(x)при x→∞ прижи-

f( 3 )0,

f(0 )0,

f(3 )0 

график функции пере-

секает ось Oxв точках

x0,x 3 . Один из возможных вариан-

тов графика такой функции имеет вид:
x

Рис. 2.6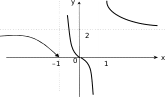

Пример 2. Используя символику теории предела, записать особенности поведения функции y = f(x), график которой изо- бражен на рис. 2.7.

Рис. 2.7