матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb.
|
|
| —10,7— 6,1 | —16,8 | 16,8 |
| 2,1 | 2,1 | 2,1 |
е) 8;
| —5,1— 1,9 | —7 | 7 |
| —2 | —2 | 2 |
) 32 И Т.Д.
На дом: №633 (в, е, и, м), 635 (в, е, и, м), 639 (ж—м).
УРОКИ 29-32. ЗАДАНИЯ 640-665
Ifenь. Создать дидактические условия для приобретения детьми опыта выполнения действий с рациональными чис- лами.
На работу с указанными выше заданиями отводится 4 урока. Рекомендуем выполнение каждого задания начи- нать с самостоятельной работы учащихся. Это позволит выяснить, как ученики усвоили материал, какие вопросы вызывают у них затруднения, на чём следует акцентировать их внимание при обсуждении результатов самостоятельной работы.
Советуем задавать на дом только те номера заданий, кото- рые обсуждались в классе. Для этого часть пунктов задания включается в классную работу, а остальные — в домашнюю. Каждое из заданий №640-665 создаёт условия для це- ленаправленного повторения ранее освоенного программ- ного материала, именно поэтому в процессе обсуждения полученных результатов советуем обращать внимание на корректное использование терминологии и правил действия
с рациональными числами.
№651, 658 — для работы в парах.
Подбирая задания к уроку, следует ориентироваться на их последовательность в учебнике, выполняя на каждом уроке не более шести номеров. Продумывая организацию деятель- ности учащихся, учитель может пользоваться методически- ми рекомендациями, данными к предшествующим урокам. На с. 146 дано определение рационального числа, для по-
нимания которого нужно выполнить №661, 662.
УPOK 33. КОНТРОЛЬНАЯ РАБОТА №7
Іfель.Проверить умения выполнять действия с рацио- нальными числами.
Примерное содержание контрольной даботы №7
ВариантI
Выполни умножение:
а) —11 0,01; 6) 18
39
Выполни деление:
—36 ; в) —7,5 (—2).
а) 9,3 (—3); 6) —
7 5
18 9 '
в) —3,8 0,1.
Найди значение выражения: а) —2,5 4 + 3 (—8);
в) —3,7 + 12 = 5,6 + 4.
б) 72 : (—9) — (—5);
Запиши каждое из чисел —7,5 и 31
2
в виде суммы двух
слагаемых: а) с одинаковыми знаками; 6) с разными знаками.
Вычисли: а) —18 — 6
—2
6) — 1+3
9 7
Запиши число —56 в виде произведения: а) двух мно- жителей; 6) трёх множителей.
Запиши число —0,2 в виде частного двух чисел.
Найди значение выражения:
а) 4 + —2.
7
6) 6 + 5 в) (—2)'; г) —4 |—5|.
ВариантМВыполни умножение:
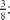а) —39 6) 0,23 (—4); в) (—2)3 0,1.Выполни деление:
а) —8,4 : (—2); 6) —54 : 6; в) —0,5 : (—0,01).
Найди значение выражения: а) (—120) : (—6) + 36 : (—12); 6) —0,03 400 + (—4,8) : (—8); в) —2,9 0 — (—75,2) + 0,2.
Запиши каждое из чисел 7,5 и —4 i
2
в виде суммы двух
слагаемых: а) с одинаковыми знаками; 6) с разными знаками.
5. Вычисли: а) —4,1+9. 6) —3— 5 .
—7 —2
Запиши число —42 в виде произведения: а) двух множителей; 6) трёх множителей.
Запиши число —0,4 в виде частного двух чисел.
Найди значение выражения:а) 8 — 1 .
—4’
6) 15 + —3. 2. г) |—2,5| (—2).
УPOK 34. АНАЛИЗ КОНТРОЛЬНОЙ РАБОТЫ №7
§ 16. Преобразование числовых и буквенных выражений
7 часов, задания 666-712
В результате изучения темы учащиеся овладеют умени- ями упрощать числовые и буквенные выражения, пользуясь правилами раскрытия скобок, свойствами сложения и умно- жения рациональных чисел; познакомятся с термином ‹по- добные слагаемые» и приобретут опыт приведения подобных слагаемых.
УPOK 35. ЗАДАНИЯ 666-673
Іfель. Познакомить учащихся с правилами раскрытия скобок в алгебраической сумме.
При выполнении заданий J"f• 666, 667, 668 школьники повторяют известные им способы преобразования числовых выражений, в основе которых лежат понятия «противопо- ложное число› и ‹алгебраическая сумма›.
he 666 обсуждается фронтально. Дети поясняют, что показывает знак «—› перед скобкой (надо записать число, противоположное числу —18,3, поэтому без скобки запишем число 18,3).
При работе с №667 и 668 ученики записывают в тетрадь выражения в виде алгебраической суммы и вычисляются их значения. При фронтальной проверке комментируются толь- ко те выражения, в которых допущены ошибки.
Дальнейшую работу учитель организует, ориентируясь на задание №669.Рекомендуем сначала выписать на доске 3-4 выражения (например: а), г), д), е)) и выяснить:
Чем похожи выражения в каждой паре?
Чем отличаются?
Чему равно значение каждого выражения?
Учащиеся обобщают результаты наблюдений и делают вывод: ‹Если в алгебраической сумме перед скобками стоит знак +, то скобки можно убрать».
Учитель ставит перед классом вопрос:
Можно ли действовать так же, если в алгебраической сумме перед скобками стоит знак ‹—» (минус)?
Ученики высказывают предположения, пытаются обосно- вать и проверить их на конкретных примерах. После этого можно открыть учебник и прочитать диалог Миши и Маши (с. 148), а таюке правила раскрытия скобок (с. 149).
№670 обсуждается устно с целью проверить, поняли ли учащиеся приведённые выше правила.
№671 (а—д), 672 (а—в), 673 (а, 6) выполняются в тетра- дях с последующей проверкой. Проверку результатов само- стоятельной работы желательно осуществлять поэтапно, то есть через каждые 2-3 выражения.
Оформляя работу в тетрадях, школьники переписывают данные в учебнике выражения, преобразуют их и находят результат. Например:
№671а) —99,8 + (17 — 19,2) = —99,8 + 17 — 19,2 = —102.
Пользуясь переместительным и сочетательным свойства- ми сложения, шестиклассники сначала устно находят сумму отрицательных чисел (—99,8 — 19,2), её значение равно —119, а затем складывают положительное и отрицательное числа 17 — 119 = —102, пользуясь соответствующим правилом.
Дети могут рассуждать и по-другому. Например, снача- ла можно выполнить действие в скобках, а затем выполнить сложение двух отрицательных чисел.
—99,8 + (17 — 19,2) = —99,8 — 2,2 = —102.
Если для некоторых детей необходимы дополнительные записи, то их можно выполнить в тетради. Например,
д) 16 — (12,2 — 3) = 16 — 12,2 + 3 = 16,8;
1) 16 + 3 = 19; 2) 19 — 12,2 = 16,8.
При работе с №673 (а) ребята сначала записывают сумму и разность данных выражений. Затем преобразуют их, поль- зуясь правилами раскрытия скобок, выполняют вычисления и затем находят значение каждого выражения при m = —0,9; п = 4,8. Запись в тетрадях выглядит так:
—3 — т+(—6 + п) = —3 — т—6 + n——9 — т+ п — —9 —
— (—0,9) + 4,8 = — 9 + 0,9 + 4,8 = —3,3.
Образец записи можно вынести на доску, рассмотрев её коллективно.
№673 (6) ученики выполняют в тетрадях самостоятельно. На дом: N671 (е—з), 672 (r—e), 673 (в, г).
УPOK 36. ЗАДАНИЯ 674-679
Іfель. Научить школьников применять правила раскры- тия скобок для преобразования числовых и буквенных вы- ранений.
После проверки домашнего задания учащиеся самостоя- тельно решают уравнения а), 6) из №674.
Применяя правило раскрытия скобок, они переписывают уравнение а) в таком виде: 4,8 — х + 6,2 — 4 = 6,8. Выполнив сложение чисел, получают уравнение 7 — х = 6,8, которое ре- шают, пользуясь соответствующим правилом.
Аналогичная работа проводится с пунктом 6).
№675 (a—r) также выполняется самостоятельно в тетра- дях. Фронтально проверяются только ответы.
В №676 (6) учащиеся повторяют понятие «модуль› (можно открыть страницу учебника и вспомнить определе- ние) и правило раскрытия скобок.
В №677 проверяется усвоение правил сложения и вы- читания рациональных чисел. Целесообразно сначала пред- ложить учащимся выполнить задание самостоятельно, затем выписать ответы на доске и обсудить их.
№678. Сначала фронтально шестиклассники анализиру- ют способ решения данного уравнения Мишей. Он приме- нил правило нахождения неизвестного вычитаемого, которое представлено в виде выражения: 4,3 — х. С этим способом учащиеся познакомились в 4 классе при решении усложнён- ных уравнений.
Маша воспользовалась новыми знаниями (правилом рас- крытия скобок).
Из уравнений, приведённых в №678 после диалога Миши и Маши, рекомендуем обсудить в классе решения уравнений 6), в), а для домашней работы — а).
№679 (а,6) — для самостоятельной работы в тетрадях. Полученные ответы выписываются на доску (как верные, так и неверные) и обсуждаются причины допущенных ошибок.
На дом: №674 (в), 676 (а), 678 (а), 679 (в, г).
УPOK 37. ЗАДАНИЯ 680-684
Lfeль. Создать дидактические условия для приобретения учениками опыта записи буквенных выражений и их преоб- разования.
После проверки домашней работы выполняется №680 (е—и). С записью буквенных выражений с числовыми коэффици- ентами дети познакомились в 5 классе, поэтому большин- ство из них сможет справиться с работой самостоятельно. Остальным учитель оказывает индивидуальную помощь (по мере необходимости).
Ученики переписывают выражения в тетрадь и, подстав- ляя значения переменных, выполняют действия с рациональ- ными числами, используя переместительное и сочетательное свойства умножения и правила умножения рациональных чисел.
№681. В процессе коллективной работы шестикласс- ники называют числовые множители, а упрощение выра- жений выполняют по вариантам: 1-й вариант — 1 столбец, 2-й вариант — 2 столбец. Результаты обсуждаются фрон- тально. Если выявляются ошибки, упрощение выражений осуществляется на доске.
№682 (a—e) выполняется самостоятельно в тетрадях. Учитель может вынести на доску ошибочные ответы, обна- руженные в некоторых тетрадях, и обсудить их.
№683. Можно организовать работу по рядам, а затем ученики каждого ряда предъявляют упрощённые выражения ребятам с других рядов, которые и оценивают результаты одноклассников.
В № 684(a—г) ученики раскрывают скобки в выражениях, пользуясь распределительным свойством умножения. Если возникают затруднения, советуем вспомнить формулировку этого свойства (умножение суммы на число или числа на сум- му) и записать несколько выражений на доске. Например:
а) —4 (2m — п) = —4 2m — 4 (—п) = —8m + 4п.
1 {b+а)
6При выполнении данного задания шестиклассники по- вторяют правила умножения рациональных чисел.
На дом: №680 (а—д), 682 (ж, и), 684 (д, е).
УPOK 38. ЗАДАНИЯ 685-691
Іfель. Познакомить учащихся с понятием «подобные сла- гаемые» и создать дидактические условия для приобретения опыта приведения подобных слагаемых.
Ориентируясь на №685, учитель записывает на доске пары выражений:
а) а(5 — 3 — 8 + 2); в) b (—10 + 4 — 5 + 1); 5п — Зп — 8п + 2п; —10b + 4b — 5b + Ь.
и обращается к ученикам:
Верно ли утверждение, что значения выражений в пун- кте а) одинаковы при любых рациональных значениях п?
Возникает проблемная ситуация. Используя распредели- тельное свойство умножения и приём аналогии, большин- ство учащихся даёт положительный ответ.
Учитель выясняет:
Как можно преобразовать первое выражение в каждом пункте?
(Сложить числа в скобках. Получаем a(—4), но так как числовой коэффициент принято писать перед буквенным множителем, запишем —4п.) Аналогичные вопросы педагог задаёт к паре выражений из пункта в).
Ориентируясь на пункты 6), г), можно вынести на доску ещё два выражения:
6) —23x + 4x — 9x + 4x; г) 3m + 8m + 15m + 9m.
и предложить ученикам записать их по-другому, используя скобки и распределительное свойство умножения. Получаем записи выражений в виде произведения двух множителей.
Теперь можно прочитать в учебнике определение подоб- ных слагаемых и правило их сложения (с. 153). Для того, что- бы понять правило и научиться применять его на практике, выполняются №686 (а—в), 687, 689 (а, 6), 690.
Советуем начинать с самостоятельной работы над каж- дым заданием. Это позволит педагогу выяснить, кто из ше- стиклассников испытывает затруднения в освоении нового материала, и скорректировать как свою деятельность, так и деятельность учащихся.
Решение уравнений в №690 учащиеся выполняют само- стоятельно в тетрадях (1 ряд — а), 2 ряд — 6), 3 ряд — в)), а затем обсуждают полученные результаты коллективно.
№691обсуждается фронтально. Дети анализируют от- веты Миши и Маши и делают вывод, что ошибку допустил
Миша, он не поменял знаки во втором и третьем слагаемых в скобках.
На дом: №686 (r—e), 688.
УPOK 39. ЗАДАНИЯ 692-696
Ifenь. Научить школьников применять правила раскры- тия скобок и приведения подобных слагаемых для преобра- зования выражений.
После проверки домашнего задания ученики выполняют самостоятельно №692 (а,6). Предварительно советуем обсу- дить план работы.
— Как будете действовать? — выясняет учитель. Примерный ответ шестиклассников:
найдём подобные члены и подчеркнём их;
приведём подобные слагаемые;
подставим значения переменных;
вычислим значение выражения.
На доску можно вынести преобразования, выполненные в п. а):
5x — 2a + 8x — За — 11х = 2x — 5п; х = —0,2; а = —0,4;
2x — 5п = 2 (—0,2) — 5 (—0,4) = —0,4 + 2 = 1,6.
№693. Уравнения а)—в) решаются самостоятельно с по- следующей проверкой результатов работы. Рекомендуем вы- полнять проверку каждого уравнения. Например:
а) (Зх — 9) + (5x — 4) = —7; Зх — 9 + 5x — 4 = —7;
8x — 13 = —7;
8x = 6;
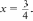
Проверка:
3 — 9) + (5 з
4 4— 4) = 9
4
— 9 + — 4 = 24
— 13 = 6 — 13 = —7.
4
№694. Сначала школьники называют в сумме каждое слагаемое и его коэффициент. Затем самостоятельно упро- щают выражения в тетрадях и переформулируют задание. (Приведи подобные слагаемые.)
Аналогично организуется деятельность класса с №695 a)—r). На дом: №687, 692 (в), 693 (r—e).
УPOK 40. ЗАДАНИЯ 697-701
Іfель. Создать дидактические условия для приобретения опыта в преобразовании буквенных выражений.
Советуем при выполнении № 697—701 ориентировать- ся на методические рекомендации, которые даны к пред- шествующим урокам темы. По своему усмотрению учитель может предложить детям проверочную работу на основе за- даний данного урока.
№697 (в, г) — в классе, (а, 6) — дома.
№701 обсуждается фронтально.
На дом: №697 (а, 6), 698 (2 столбец), 700 (2 столбец).
УРОКИ 41, 42. ЗАДАНИЯ 702-712
Іfель. Повторить ранее изученный материал (запись дробных выражений, алгебраической суммы, нахождение части от целого и т. д.)
После проверки домашнего задания обсуждается №702. Ученики анализируют записи Миши и Маши и отвечают на вопрос задания. (Маша подставила значение х в данное выражение. Миша сначала преобразовал данное выражение, а потом подставил значение х.) Вывод: можно пользоваться и одним, и другим способом. Для данного выражения эти способы равнозначны.
Рекомендуем после работы с №702 записать на доске различные выражения и обсудить, каким способом луч- ше пользоваться при вычислении их значений. Например, нужно найти значение выражения —Зх + 4-2 + 5x — 8x при х = —4. Здесь лучше сначала выполнить преобразования:
—6x + 2, а затем подставить значение х: —6 (—4) + 2 = 26.
№703 — для самостоятельной работы. Его успешное выпол- нение будет свидетельствовать о том, что школьники понима— ют, как можно получить данное выражение. В случае затруд- нений пункт а) можно обсудить, пользуясь записью на доске:
| 5x— 4 | 5x _ 4 | 5x _ 1 |
| 12 | 12 12 | 12 3 |
Рекомендуем из №704 обсудить в классе два числа: 5,4 и —3,8, а остальные числа включить в домашнюю работу. Дети самостоятельно записывают в тетрадях двойные нера- венства.
№705 можно выполнить устно или обсудить после того, как ученики самостоятельно запишут в тетрадях три пары чисел, соответствующих условию задания. Советуем при проверке №704, 705, 706 воспользоваться координатной прямой.
При выполнении №707 учащиеся выписывают на доске различные пары чисел и для обоснования своего ответа от- мечают на координатной прямой точки, соответствующие этим числам.
№708. Работа над ним покажет, усвоили ли ученики запись буквенных выражений с коэффициентом. В этот же урок желательно включить задания № 709—712.
На дом: №703 (ж—м), 706 (6).