Пример рабочей программы
курса математики
6 класса
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
«Медагогмческая наука ммеет только два выхо-да в практик у: либочерездеятельностьучите- ля (если он эту на ук у усвомл),либо черезучебник (если он nocmpoeн на её“ основе). Мобильность учмтеля в освоеним педагогмческой наукм и пре- твореним eè“в практик у минммальна:существy- ет мнение, что для освоения новой методикм преподаванияучителю требуется от 5 до 7лет работы.Следовательно,основнойвыходнаукмв практмк у — через учебники методик у его по- строения›.
В. П. Беспалько, Теория учебника, М., 1988
Предлагаемый примерный вариант рабочей программы рас- сматривается авторами как средство помощи учителю, работаю- щему по учебникам математики Н.Б. Истоминой, в организации учебного процесса, направленного на достижение планируемых результатов, предусмотренных ФГОС ООО.
При составлении данного варианта рабочей программы ав- торы ориентировались на комплекс требований Федерального государственного образовательного стандарта основного общего образования, на Примерную основную образовательную про- грамму основного общего образования, на ведущие идеи Кон- цепции развития математического образования в Российской Федерации.
В предлагаемом учебно-методическом комплекте по мате-
матике для 5-6 классов получает дальнейшее развитие та ме- тодическая концепция обучения, которая реализована в ком- плекте для 1-4 классов (автор профессор Н.Б. Истомина). Суть данной концепции заключается в целенаправлен- ном развитии мышления всехучащихсяв процессе усвоения
программного математического содержания.
 4
Критериями развития мышления в русле данной концеп- ции является сформированность таких приёмов умствен- ной деятельности как анализ и синтез, сравнение, аналогия, классификация и обобщение. По мнению психологов, ов- ладев этими приёмами, ученики становятся более самосто- ятельными в решении учебных задач (локальных, частных, общих, перспективных) и могут рационально строить свою деятельность, направленную на овладение универсальными учебными действиями (познавательными, регулятивными, коммуникативными) в процессе усвоения предметного со— держания.
Единая методическая концепция курсов ‹Математика› 1-4 и «Математика» 5-6 классов обусловлена и их одно- имённым названием, и необходимостью создания дидакти- ческих условий для преемственности обучения математике в начальной и основной школе не только в плане предметно- го содержания, но и в плане способов организации учебной деятельности учащихся.
Для разъяснения заявленной методической концепции необходимо обратиться к психологической науке, которая убедительно доказала, что психическое развитие человека (в особенности умственное) происходит только в ходе пре— одоления препятствий, интеллектуальных трудностей, удов- летворения потребности в приобретении новых знаний. Результаты исследований показали, что одним из главных условий, обеспечивающих развитие мышления учащихся в процессе обучения, является nocmaпoвкaпроблежпыхза-даний,вызывающих проблемные ситуации. При этом следу- ет иметь в виду, что понятия «проблемное задание› и «про- блемная ситуация» не тождественны. Проблемная ситуация характеризует психическое состояние школьника, связанное с началом его мыслительной деятельности. Основными ком- понентами проблемной ситуации являются: неизвестное, которое должно быть раскрыто (найдено), потребность уча- щихся ‹открыть» это неизвестное и их возможности проана- лизировать требования задания, чтобы ‹открыть» это новое. К сожалению, методисты крайне редко пользуются по- нятием «проблемная ситуация». Но при разработке проблем- ных заданий важно предвидеть именно ту проблемную си- туацию, которая возникает в процессе выполнения детьми данного задания. Зачастую к проблемным заданиям методи- сты (и учителя математики) относят нестандартные задачи
 5
или задачи повышенной трудности. Однако не всякую не- стандартную задачу можно назвать проблемным заданием, а только ту, которая создаёт проблемную ситуацию, то есть, как было сказано выше, вызывает определённое психиче- ское состояние ученика, представляющее собой неразрывное единство познавательных и аффективных (эмоционально- волевых) аспектов.
Безусловно, результаты исследования психических про- цессов, в частности, процесса мышления, не могут непо- средственно внедряться в практику обучения. Необходи- ма разработка соответствующей методической концепции и конкретных методических подходов, одним из которых яв- ляется система заданий, создающих проблемные ситуации.
Таким образом, пробпеліное задание — необходиліый кожпопепт процесса обу•tепияцелью которого является развитиемышлениявсехучащихся.
С методической точки зрения включение проблемных заданий в учебный процесс требует прежде всего принятия учителем определённой позиции в отношении процесса ус- воения детьми новых знаний, которая связана с ответом на вопросы:
Как предлагать ученику знания, которые он должен усвоить?
Что ученику надо сделать для того, чтобы усвоить эти знания?
В зависимости от ответа на эти вопросы можно выделить две позиции.
В одном случае знание (факты, правила, определения, способы действий) предлагается ученикам в виде известного учителю образца, который они должны запомнить и воспро- извести. Затем путём тренировочных упражнений ‹отрабо- тать» соответствующие умения (навыки).
В другом случае ученик сначала включается в деятель- ность, у него возникает потребность в освоении новых зна- ний, и он добывает их сам или с помощью учителя.
Например, школьник успешно освоил сравнение дробей с одинаковыми числителями или одинаковыми знаменате-
лями, то есть выполнение задания: «Сравни дроби
5 7 7
3 5 7
8 И 8 12
И 12 9 И 13 » не вызывает затруднений, так как он усвоил способ действий. Но если для сравнения предлагаются дроби 6
5 9
7 И 2 то ситуация изменяется и становится проблемной, так как способ сравнения дробей с разными числителями и разными знаменателями ученику пока неизвестен. На дан- ном этапе это задание можно рассматривать как проблемное: возникает трудность, препятствующая продвижению вперёд.
Конечно, для разных учеников степень этой трудности будет различной. Это зависит от двух факторов: от сформирован- ности мыслительных операций (анализ, синтез, сравнение, обобщение) и от тех знаний, которыми школьник овладел. В данном случае от того, знаком ли он с понятиями «пра- вильная дробь», ‹неправильная дробь» и умеет ли перево- дить неправильную дробь в смешанное число.
Некоторые учащиеся смогут самостоятельно вскрыть суть появившихся изменений и сформулировать стоящую перед ними задачу: ‹Как нужно действовать, чтобы сравнить пра- вильную и неправильную дроби?» Другим понадобится по- мощь учителя. Но эта помощь заключается не в том, чтобы учитель дал своим подопечным информацию, содержащую подсказку о способе выполнения: «Посмотрите внимательно: одна дробь правильная, а другая неправильная› или «Давай- те вспомним, какую дробь мы называем правильной, а ка- кую неправильной».
Целесообразнее предложить школьникам вспомогатель- ные вопросы, создающие дидактические условия для акти- визации мышления. К примеру, записав ещё несколько пар дробей, педагог предлагает выяснить, чем похожи все пары дробей и чем отличаются. Изобразив данные в каждой паре дроби на координатном луче, ученики самостоятельно дела- ют вывод: любая неправильная дробь всегда больше любой правильной дроби.
Главный механизм этого ‹открытия» — образование но- вых связей, так как неизвестное (свойство, отношение, за- кономерность, способ действия) раскрывается только че- рез установление связей с уже известными. Таким образом, поиск неизвестного — это постоянное включение объекта во все новые системы связей.
Важным методическим условием осуществления этих связей является целенаправленное и систематическое вклю- чение в учебный процесс последовательности проблемных заданий, при выполнении которых ученик повторяет ранее изученный материал, активно мыслит и, наконец, может сам
7
сформулировать новую учебную задачу и решить её само- стоятельно или с помощью учителя. Так, после сравнения правильных и неправильных дробей многие учащиеся спо- собны сами поставить проблемный вопрос: «Как нужно дей- ствовать, чтобы сравнить две правильные дроби с разными
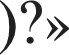 числителями и знаменателями (например, 13 И 9
40 32
Постановка подобного вопроса создаёт ситуацию, кото- рую можно назвать проблемной, так как она содержит:
неизвестное, требующее нового способа действия;
потребность «открыть» это неизвестное;
возможность справиться с предлагаемой учебной зада- чей, используя для этой цели ранее изученные вопросы (на- хождение HOK и основное свойство дроби).
Осознание учениками стоящей перед ними задачи, целе- направленное повторение ранее изученного материала для
‹открытия» нового способа действия создают основу для по- нимания и усвоения той последовательности действий, ко- торая связана с приведением дробей к общему знаменателю. Описанный выше процесс выполнения проблемных за- даний можно соотнести с традиционным этапом ‹объясне- ние нового материала», но при этом следует отметить суще— ственные отличия этой работы от объяснения, при котором
педагог сообщает и разъясняет готовые знания.
Творчески работающий учитель, как правило, редко обра- щается кобъяснительным текстам. Он пытается сам продумать объяснение нового материала так, чтобы активизировать по- знавательную деятельность учащихся. Школьники при этом заглядывают в объяснительные тексты учебника только для того, чтобы вспомнить то или иное правило или определение. Функции, объём, содержание и задачи авторского объяс- нительного текста, с которого начинается каждый параграф, неоднократно обсуждались в методической литературе. Мо- дернизация данного компонента нашла отражение в учебни- ке-собеседнике (Л. Н. Шеврин, А. Г. Гейн). Авторы ставили сво- ей целью построить учебник таким образом, чтобы дети «не только приобретали знания и навыки, но и учились мыслить». В предлагаемых учебниках математики для 5-6 классов нашёл отражение так называемый задачный подход, при ко- тором основным средством включения учащихся в актив- ную познавательную деятельность являются учебные задачи
(перспективные, общие, частные, локальные). Одни из них подготавливают школьников к восприятию нового знания, другие создают проблемные ситуации, третьи обеспечивают комфортные дидактические условия для понимания и усвое- ния учебного материала, четвёртые способствуют организации продуктивного повторения, то есть повторения, необходимого для решения новой учебной задачи или для осознания взаи- мосвязи между изучаемыми вопросами, пятые предназначены для самостоятельной работы учащихся и т. д.
Поэтому изучение нового материала в учебниках матема- тики 5-6 классов начинается не с объяснительного текста, а с задания или заданий, выполнение которых связано с ис- пользованием различных приёмов умственной деятельности (анализ и синтез, сравнение, классификация, аналогия, обоб- щение), готовящих учащихся к восприятию нового понятия, термина, определения и т. п., либо с проблемного задания.
Создавая проблемную ситуацию, такое задание ставит пе- ред школьниками новую учебную задачу, которую они реша- ют самостоятельно или с помощью учителя, или им помогают Миша и Маша (персонажи учебника), чьи диалоги и рассуж- дения включены в задания. Заметим, что подобному приёму предшествовала большая исследовательская работа, в процес- се которой учебные задания предлагались сотням учеников, обучающихся по разным программам. Их ответы подверга- лись обработке: анализировались, классифицировались, кор- ректировались и включались (или не включались) в учебник. Более того, анализ ответов учащихся позволил также скор— ректировать формулировки некоторых заданий.
Важно обратить внимание на следующее: если после формулировке задания дано указание: «Сравни свой ответ (или свои рассуждения) с ответами (рассуждениями) Миши и Маши», это значит, что сначала ученики формулируют свои рассуждения и только после этого знакомятся с высказывани- ями Миши и Маши, диалог которых позволяет скорректиро- вать ответы школьников или оказывает помощь тем, кто ис- пытывает затруднения при выполнении задания.
С психологической точки зрения это существенно: не учитель помогает, если трудно, а ‹одноклассники» — Миша и Маша. Присутствие этих персонажей делает учебник более доступным и понятным учащимся, и они проявляют боль- ший интерес к диалогам Миши и Маши, нежели к объясни- тельному авторскому тексту.
9
Традиционно после знакомства с новым материалом сле- дует этап его закрепления, во время которого школьники, как правило, выполняют тренировочные задания (их образ- цы обычно приводятся в объяснительном тексте учебника). Однако с точки зрения психологии усвоения после знаком- ства с новым материалом необходима деятельность, нацелен- ная прежде всего на его понимание. Процесс же понимания требует выполнения не однотипных упражнений, а продук- тивной мыслительной деятельности. Она вызывается вариа- тивными заданиями, в процессе работы над которыми дети устанавливают взаимосвязи между новым и ранее изучен- ным материалом. Здесь опять ‹появляются» Миша и Маша, которые предлагают различные способы выполнения того или иного задания (при этом в зависимости от специфики математического содержания один способ может быть вер- ным, а другой — неверным; оба способа верные, но один из них нерациональный и т. д.).
В учебниках математики 5-6 классов так же, как и в учеб- никах 1-4 классов (автор Н. Б. Истомина), повторение не выде- ляется в отдельный этап, а органически включается в каждый компонент учебной деятельности: постановку учебной задачи, решение учебной задачи (понимание, принятие, усвоение), самоконтроль.
Следуя идеям уровневой дифференциации, авторы ряда учебников математики 5-6 классов группируют задания на применение нового материала по уровням сложности. В этом случае задания, например, группы А, носят репродуктивный характер, а группы Б являются более сложными, требующи- ми продуктивной деятельности.
Возникает вопрос: насколько целесообразен такой подход в учебниках математики 5-6 классов с психологической точ- ки зрения?
Дело в том, что в большинстве случаев он (то есть такой подход) формирует не познавательный интерес у учащихся, а заниженную самооценку или «престижную мотивацию». Задания группы Б чаще всего не обсуждаются в классе (на них просто не хватает времени), поэтому учитель предла- гает их обычно только тем учащимся, которые могут с ними справиться самостоятельно, или включает эти задания в до— машнюю работу в надежде на помощь родителей. Ученик же, который не может выполнить эти задания, постепенно теряет веру в свои возможности и приобретает комплекс
10
заниженной самооценки, и даже не пытается приступать к ним при изучении последующих тем.
В представленных учебниках математики 5-6 классов дифференцированный подход находит отражение в способах организации деятельности учащихся, направленной на вы- полнение различных видов учебных заданий. Одни из них носят проблемный характер. Другие выполняются с исполь- зованием различных моделей: вербальной, графической, схе- матической и символической; третьи предполагают выбор правила, свойства, определения для обоснования способа деятельности или содержат дополнительные вопросы и т. д. Все эти задания носят обучающий характер и положительно влияют на познавательную деятельность школьников.
В предлагаемых учебниках математики 5-6 классов не вы- деляется рубрика с домашними заданиями, так как содержание домашней работы во многом зависит от того, как дети работали на уроке, и учитель может и должен решить этот вопрос сам. Главное, чтобы дома ребёнок мог выполнить предложенные задания самостоятельно, не прибегая к помощи родителей. Итак, предлагаемые учебники математики 5-6 классов представляют собой систему задач, нацеленных на развитие мышления, в процессе выполнения которых школьники ус- ваивают знания, умения и навыки и овладевают способами
познавательной деятельности.
Учебник математики для 5 класса содержит четыре гла- вы: ‹Натуральные числа и нуль›, «Обыкновенные дроби»,
‹Десятичные дроби», ‹Таблицы и диаграммы».
В учебнике математики для 6 класса — три главы: «Обык- новенные и десятичные дроби», «Рациональные числа»,
«Элементы теории множеств и комбинаторики».
Главы построены тематически (разбиты на параграфы). Каждая следующая тема (параграф) не только связана с пре- дыдущей, но и с тем предметным содержанием, который из- учался в начальной школе.
Такая структура учебников математики 5-6 классов по- вышает степень самостоятельности учащихся при решении новых учебных задач и создаёт дидактические условия для освоения предметных и метапредметных умений, основным средством формирования которых являются учебные зада- ния. Они нацеливают учеников на выполнение различных видов деятельности, формируя тем самым умение действо- вать в соответствии с поставленной целью.
Учебные задания побуждают детей анализировать объ- екты с целью выделения их существенных и несуществен- ных признаков, выявлять их сходство и различие, проводить сравнение и классификацию по заданным или самостоя- тельно выделенным признакам (основаниям), устанавливать причинно—следственные связи, строить рассуждения в фор- ме простых суждений об объекте, его структуре, свойствах; обобщать, то есть осуществлять генерализацию для целого ряда единичных объектов на основе выделения сущностной
сВЯзи.
Для облегчения работы с учебниками математики 5-6 классов в его текст вклк›чены специальные символы, харак- теризующие особенности организации учебной деятельности школьников при выполнении заданий учебника.
Самое распространённое условное обозначение в учебни- ках математики для 5-6 классов так же, как и в учебниках математики для 1-4 классов, — это изображение персонажей Миши и Маши.
  Задания, отмеченные этим знаком, выполня- ют различные функции: их можно использовать для само- контроля и коррекции ответов учащихся, для получения новой информации, овладения умением вести диалог, для разъяснения способа решения задачи и др.
В процессе чтения, анализа и обсуждения диалогов и вы- сказываний Миши и Маши учащиеся не только усваивают предметные знания, но и приобретают опыт построения понятных для партнёра утверждений, учитывающих, что он знает и видит, а что — нет; учатся задавать вопросы, ис- пользовать речь для регуляции своего действия, формулиро- вать собственное мнение и позицию, контролировать дей- ствия партнёра.
Для введения новой информации используется знак , для актуализации ранее усвоенной информации —  '
Деятельность, требующая самоконтроля, обозначается знаком .
Символом Ф обозначаются дополнительные задания или вопросы к основному заданию.
 Деятельность учащихся в парах обозначается так:
Для обозначения исследовательских заданий, связанных с наблюдением, экспериментом, обобщением, решение кото- рых основано на выдвижении и анализе гипотез, использу-
ется знак .
Знаком выделены задания, выполнение которых тре-
бует поиска исторического материала в энциклопедиях, спра- вочниках, журналах и сети интернет. Как правило, эти зада- ния предназначены для домашней работы и выполняются по желанию учащихся. Результаты поиска ученики оформляют в виде сообщений (презентаций). Вопросы, связанные с исто- рией математики, являются основополагающими для органи- зации проектно-исследовательской деятельности.
Обозначения , подсказывают детям, когда целе- сообразно использовать данные инструменты.
Знак Щ обозначает задания повышенной сложности, ко- торые характеризуются новизной формулировки, и требуют установления взаимосвязей между различными вопросами курса математики.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ОБУЧЕНИЯ МАТЕМАТИКЕ
НА КОНЕЦ ШЕСТОГО КЛАССА
ЛИЧНОСТНЫЕ РЕЗУЛЬТАТЫ
освоения предмета ‹Математика› на конец 6 класса: внутренняя позиция положительного и ответственного
отношения к учению;
учебно-познавательный интерес к новому материалу и способам решения новой учебной задачи;
готовность целенаправленно использовать математи- ческие знания, умения и навыки в учебной деятельности и в повседневной жизни;
способность осознавать и оценивать свои мысли, дей- ствия и выражать их в речи, соотносить результат действия с поставленной целью;
способность к организации самостоятельной деятель-
НОСТИ;
готовность и способность к саморазвитию и самообра- зованию;
осознанное, уважительное и доброжелательное отно- шение к другому человеку, его мнению;
готовность и способность вести диалог с другими людьми и достигать в нём взаимопонимания.
Изучение математики будет способствовать формирова- нию таких личностных качеств как любознательность, тру- долюбие, способность к организации своей деятельности и к преодолению трудностей, целеустремлённость и настойчи- вость в достижении цели, умение слушать и слышать собесед- ника, обосновывать свою позицию, высказывать своё мнение.
МЕТАПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ
освоения предмета ‹Математика› на конец 6 класса
Регулятивные универсальные учебные действия:
принимать и сохранять учебную задачу;
планировать (в сотрудничестве с учителем или само- стоятельно, в том числе во внутренней речи) свои действия для решения задачи;
действовать по намеченному плану, а также по ин- струкциям, содержащимся в источниках информации;
контролировать процесс и результаты своей деятельно- сти, вносить необходимые коррективы;
оценивать свои достижения, осознавать трудности, ис- кать их причины и способы преодоления;
анализировать существующие и планировать будущие образовательные результаты.
Познавательные универсальные учебные действия:
определять понятия, создавать обобщения, устанавли- вать аналогии, самостоятельно выбирать основания и крите- рии для классификации, устанавливать причинно—следствен- ные связи, строить логические рассуждения, умозаключения (индуктивные, дедуктивные, по аналогии) и делать выводы;
осознавать познавательную задачу, целенаправленно слушать (учителя, одноклассников), решая её;
находить в тексте необходимые сведения, факты и дру- гую информацию, представленную в явном виде;
самостоятельно находить нужную информацию в ма- териалах учебника, в учебной литературе, использовать её для решения учебно—познавательных задач;
использовать знаково-символические средства, в том числе модели и схемы, для решения задач;
ориентироваться на разнообразие способов решения
задач;
осуществлять анализ объектов с выделением суще- ственных и несущественных признаков;
осуществлять синтез как составление целого из частей; устанавливать причинно—следственные связи;
строить рассуждения в форме простых суждений об объекте, его строении, свойствах и связях;
осуществлять подведение под понятие на основе рас- познавания объектов, выделения существенных признаков и их синтеза;
владеть общим приёмом решения задач;
применять разные способы фиксации информации (словесный, схематический); использовать эти способы в процессе решения учебных задач.
Коммуникативные универсальные учебные деиствия:
участвовать в диалоге, в общей беседе, выполняя при- нятые правила речевого поведения (не перебивать, выслуши- вать собеседника, стремиться понять его точку зрения и т. д.);
выражать в речи свои мысли и действия;
строить понятные для партнёра высказывания, учиты- вающие, что партнёр видит и знает, а что нет;
задавать вопросы;
использовать речь для регуляции своего действия;
строить небольшие монологические высказывания с учётом ситуации общения.
ПРЕДМЕТНЫЕ РЕЗУЛЬТАТЫ
освоения предмета ‹Математика› на конец 6 класса:
оперировать на базовом уровне понятиями: натуральное число, целое число, обыкновенная дробь, десятичная дробь, смешанное число, рациональное число;
использовать свойства чисел и правила действий с раци- ональными числами при выполнении вычислений;
использовать признаки делимости на 2, 5, 3, 9, 10 при вы- полнении вычислений и решении несложных задач;
выполнять округление рациональных чисел в соответ- ствии с правилами;
сравнивать рациональные числа;
понимать и объяснять смысл позиционной записи на- турального числа;
оперировать понятиями: равенство, числовое равенство, уравнение, корень уравнения, решение уравнения, числовое неравенство;
решать несложные сюжетные задачи разных типов на все арифметические действия;
строить модель условия задачи (в виде таблицы, схемы, рисунка) с целью поиска решения задачи;
осуществлять способ поиска решения задачи, в котором рассуждение строится от условия к требованию или от требо- вания к условию;
знать различие скоростей объекта в стоячей воде, против течения и по течению реки;
решать задачи на нахождение части числа и числа по его части;
решать задачи разных типов (на работу, на покупки, на движение), связывающие три величины, выделять эти величины и отношения между ними;
находить процент от числа, число по проценту от него, на- ходить процентное отношение двух чисел, находить процентное снижение или процентное повышение величины;
решать несложные логические задачи методом рассуж- дений;
оценивать результаты вычислений при решении прак- тических задач;
выполнять измерение длин, расстояний, величин углов с помощью инструментов для измерений длин и углов;
вычислять площади прямоугольников, объёмы прямоу— гольных параллелепипедов, кубов;
оперировать на базовом уровне понятиями: фигура, точка, отрезок, прямая, луч, ломаная, угол, многоугольник, треуголь- ник и четырёхугольник, прямоугольник и квадрат, окружность и круг, прямоугольный параллелепипед, куб, шар;
изображать изучаемые фигуры от руки и с помощью ли- нейки и циркуля;
решать практические задачи с применением простейших свойств фигур;
представлять данные в виде таблиц, диаграмм;
читать информацию, представленную в виде таблицы, диаграммы;
оперировать на базовом уровне понятиями: множество, элемент множества, подмножество, принадлежность;
задавать множества перечислением их элементов;
находить пересечение, объединение, подмножество в про- стейших ситуациях;
находить отдельные выдающиеся результаты, полученные в ходе развития математики как науки;
представлять данные в виде таблиц, диаграмм;
читать информацию, представленную в виде таблицы, диаграммы.
СОДЕРЖАННЕ KУPCA MATEMATHKH.
|
Скачать 2.01 Mb.