матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb. Скачать 2.01 Mb.
|
|
В результате изучения темы шестиклассники овладеют умением находить среднее арифметическое чисел. Большинство детей интуитивно представляет, о чём идёт речь, когда говорят ‹средний возраст», ‹средний рост›, ‹средний заработок», •средний балл», ‹средняя скорость». Изучение данной темы позволяет уточнить имеющиеся у школьников представления, познакомить их с понятием «среднее арифметическое» и связать его с ранее усвоенными вопросами. УPOK 23. ЗАДАНИЯ 146-150 Јfель.Познакомить учащихся с правилом нахождения среднего арифметического чисел. Первый урок целесообразно начать с фронтального об- суждения словосочетаний «средний возраст», «средний рост», «средний заработок», заранее записанных учителем на доске. Далее следует перейти к комментарию ситуации из №146 (учитель выписывает на доску отметки Коли). Советуем сна- чала выслушать ответы ребят, а затем прочитать рассужде- ния Миши и Маши. Учитель знакомит ребят с определением среднего арифметического чисел и, записав на доске выражения вида (15,5 + 16,8) 2; (15,5 + 16,8) 15,5; (15,5 + 16,8) : 16,8; (15,5 + 16,8) : 2, предлагает учащимся выбрать и записать в свои тетради то выражение, в котором находят среднее арифметическое двух чисел. Не следует торопиться с вы- зовом к доске ученика, который сможет объяснить способ действия. Желательно через 1,5-2 минуты выяснить, какое выражение появилось в тетрадях у детей. Для обоснования ответа шестиклассники ссылаются на определение среднего арифметического, данное на с. 32 учебника. № 147 (а—в) учащиеся выполняют самостоятельно в те- традях. №148, как показывает практика, вызывает затруднения у многих детей. В такой ситуации целесообразно проанализи- ровать рассуждения Миши и Маши, приведённые в учебнике. Это позволит учащимся понять, как нужно действовать при решении не только данной задачи, но и № 150. С № 149 ученики работают самостоятельно, выполняя вычисления в тетрадях. Предложив №150 для самостоятельной работы, мож- но проверить, как учащиеся усвоили содержание понятия ‹среднее арифметическое». Записав решение задачи в тетра- дях, ребята выписывают на доске только ответы. Они могут быть верными или неверными. При обсуждении учитель вы- ясняет, как получены и верные, и неверные ответы. Полез- но уточнить, что обозначают числа 6,4 и 4,8 (6,4 — среднее арифметическое шести чисел, а 4,8 — среднее арифметиче- ское двух чисел). Полученный ответ следует соотнести с определением среднего арифметического, и учащиеся поймут ту ошибку, которую они допустили. Если большая часть класса не справилась с заданием, то можно использовать приём обсуждения решения задачи и записать на доске действие: 6,4 6 = 38,4, а ученики объяс- нят полученный результат и продолжат решение задачи. На дом: № 147 (r—e). УPOK 24. ЗАДАНИЯ 151-155 Іfель. Создать дидактические условия для усвоения деть- ми определения среднего арифметического двух чисел. После проверки домашнего задания учащиеся самосто- ятельно выполняют в тетрадях № 153. На доске они выпи- сывают полученные ответы, которые могут быть как верны- ми (3,9), так и неверными. Советуем не записывать решение на доске. Целесообразно обсудить его фронтально при обо- сновании ответов, полученных детьми. Рекомендуем рассмотреть на уроке задачи «на движение» по течению и против течения реки и подвести учащихся к выводу, что собственная скорость того или иного объекта является средним арифметическим его скорости по течению и против течения. Ученики уже решали такие задачи в 5 классе, пользу- ясь схемой. Поэтому текст задачи № 152 рекомендуем по- местить на доску и предложить шестиклассникам запи- сать самостоятельно её решение. Дальнейшую деятельность класса учитель организует в зависимости от результатов са- мостоятельной работы, на выполнение которой отводится 5-7 минут. АI I см   Анализируя каждую схему, ученики обозначают на ней известные и неизвестные в задаче величины. После прове- дённой работы изображённые на доске схемы приобретают такой вид: ,'D ,N Комментируя каждую схему, шестиклассники отмечают, каким отрезком обозначена собственная скорость теплохода, каким — его скорость по течению реки, каким — скорость против течения реки. Пользуясь схемой, большинство учащихся самостоятель- но записывает решение задачи тем способом, который пред- ложен в учебнике Машей. Вполне возможно, что некоторые ребята запишут реше- ние задачи другим способом. Теперь можно открыть учебник и прокомментировать те способы решения задачи, которые предложены Мишей и Машей. Задачу №154 ученики решают самостоятельно двумя спо- собами, ориентируясь на способы Миши и Маши в № 152. № 155 обсуждается устно. На дом: № 151. § 3. Дробные выражения 3 часа, задания 156-171 В результате изучения темы у школьников формиру- ются представления о дробных выражениях, о способах их преобразования и совершенствуются вычислительные уме- ния и навыки. УPOK 25. ЗАДАНИЯ 156-159, 166 (r—e) Іfель. Познакомить шестиклассников с понятием ‹дроб- ное выражение». Повторить правила действий с дробями и решение уравнений. Рекомендуем начать урок с №156, который большинство учащихся могут выполнить самостоятельно. Задание подго- тавливает детей к восприятию нового понятия. Предложенные учениками варианты выражений выно- сятся на доску. Затем школьники открывают учебник, выби- рают те выражения, которые соответствуют условию, читают определение дробного выражения и следующий за ним ав- торский текст. С №157 организуется фронтальная работа. Учащиеся, комментируя действия Миши и Маши, отмечают, что Миша записал частное в виде дроби, предварительно обыкновен- ную дробь представил в виде десятичной. Затем Миша ум- ножил и числитель, и знаменатель на 100, сократил полу- ченную дробь на 3. Далее Миша представил неправильную дробь в виде смешанного числа, после чего записал резуль- тат в виде десятичной дроби. Маша применила правило деления числа на обыкновен- ную дробь. В полученном дробном выражении она выполни- ла сокращение, затем — умножение в числителе и записала результат. Проведённое обсуждение служит подготовкой к работе с № 158. Рекомендуем, прочитав задание, обсудить различные способы вычисления значений выражений. Например, в пункте а) можно сначала воспользоваться ос- 75 15 5 новным свойством дроби, умножив числитель и знаменатель на 10 3 30 7,5 75 , затем сократить полученную дробь 30 6 2 А можно сразу выполнить деление числителя на знаменатель, воспользовавшись правилом деления на десятичную дробь: 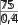 3 7,5 = 30 75. 30 3 7,5 = 30 75. 30 300 300 0 Второй способ будет рациональным. В пункте г) необходимо сначала выполнить действие в числителе, затем в знаменателе, а потом разделить ре- зультат, полученный в числителе, на результат, полученный в знаменателе. 18— 6,2 11,8 11,8; 11,8 0,5 118 5 23,6. 9 + 0,05 0,45 + 0,05 0,5 20 В пункте е) следует обратить внимание на то, что в зна- менателе дробного выражения нужно производить вычисле- ния в соответствии с правилами порядка выполнения дей- стВИй. № 159 дети выполняют самостоятельно (в классе пункты (a—r), дома — пункты (д—з)). Также самостоятельно ученики могут записать решение уравнений №166 (6, г, е), пользуясь правилами нахождения неизвестного компонента и действий с дробями. Например: 6) 2 х = 32; г) 27 х = 2,5; е) х — 89 = 5 18 х = 32 2 ; 2 3 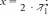 iq 3 iq 3х = 27 22; 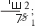 *" *" 5 + Советуем в каждом уравнении записать корень в виде дробного выражения и, выполнив соответствующие преоб- разования, убедиться в том, что получится тот же результат. Например: 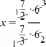 6) 2 - х = 32; 6) 2 - х = 32;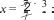 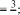 2› 2›На дом: № 159 (д—з), 166 (а, в, д). УPOK 26. ЗАДАНИЯ 160-165 Ifenь. Формировать умение выполнять преобразования дробных выражений. В начале урока проверяется домашнее задание. Советуем вынести на доску запись корня каждого уравнения в виде дробного выражения и выполнить с ним необходимые пре- образования. Преобразование дробных выражений является не только полезным вычислительным упражнением, но и создаёт ус- ловия для повторения ранее изученных вопросов (основное свойство дроби, сокращение дробей, признаки делимости и пр.). №163 обсуждается фронтально. В этот же урок советуем включить № 164 (в, г), предвари- тельно обсудив способы действия Миши и Маши (с. 36 учеб- ника). На дом: № 160 (г—и), 161 (г, д), 165 (а—в). УPOK 27. ЗАДАНИЯ 167-171 Ifenь. Продолжить формирование умения выполнять дей- ствия с дробными выражениями. №167 рекомендуем вынести на доску и обсудить коллек- тивно все возможные сокращения, при этом обыкновенные дроби в каждом пункте лучше записать в виде десятичных. Например: а) 2 5 3,1 6 5 1,2 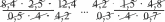 1 1 1 1 1 1 1 1 1 1 1 131 36 100 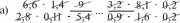 Tf 1 1 2 9 1 Tf 1 1 2 9 12 1 i °"* 1 1 1 50 18 № 168 предупреждает типичную ошибку, которая обыч- но допускается школьниками при сокращении дробных выражений. Следует обсудить каждое дробное выражение и обратить внимание на то, что сокращать можно только множители, так как сокращение — это деление числителя и знаменателя дроби на одно и то же число. № 171 советуем предложить для самостоятельной работы в парах: дети читают условие и обсуждают каждое из дроб- ных выражений, после чего делают вывод. Одни могут за- метить, что в дробном выражении а) и в числителе, и в зна- менателе из 10,25 вычитают выражение, значение которого равно 0. Другие, анализируя данное дробное выражение, об- наружат, что из 10,25 вычитают одинаковые выражения, в которых выполняются одни и те же действия. Комментируя пункт 6), шестиклассники повторяют пере- местительное свойство умножения, запись числа в эквива- лентной форме, запись обыкновенных дробей в виде деся- тичных (и наоборот). В №169 сначала обсуждается способ действия, затем уче- ники самостоятельно находят значение дробных выражений. В № 170 нужно найти значения буквенных выражений при данных значениях п или Ь. Ввиду того, что преобразование дробных выражений яв- ляется для учащихся трудоёмкой работой, учитель может распределить эти упражнения во времени и включить их во все последующие уроки. На дом: № 170 (а—в). УPOK 28. КОНТРОЛЬНАЯ РАБОТА №2 Іfель. Проверить сформированность умений: округлять десятичные дроби, записывать обыкновенные дроби в виде десятичных, выполнять преобразования в дробных выраже- ниях; усвоение понятия «среднее арифметическое чисел›. Примерное содержание контрольной работы №2 ВармантI Округли числа 54,2874; 2,8469: а) до целых; 6) до деся- тых; в) до сотых; г) до тысячных. Сравни десятичные дроби, поставив знаки , или = а) 0,60 0,600; в) 9,805 9,8; 6) 6,08 ... 6,080; г) 5,01 ... 5,011. Сравни дроби, поставив знаки или К. а) 7 20 0,3; 6) 0,3 6 25 з 0,7. Среднее арифметическое двух чисел равно 4,5. Одно число равно 1,2. Найди другое число. Найди значение дробного выражения: 3,2  а) 0,5 а) 0,520 12,4 4 6,4 5 7  Скорость теплохода по течению реки равна 26 км/ч, а против течения — 22 км/ч. Какое расстояние тепло- ход пройдет по озеру за 1,2 часа? ВармантII Округли числа 27,3845; 0,54367: а) до целых; 6) до деся- тых; в) до сотых; г) до тысячных. Сравни десятичные дроби, поставив знаки +, или = а) 9,02 9,022; в) 3,09 3,090; 6) 7,301 ... 7,3; г) 0,4 ... 0,400. Сравни дроби, поставив знаки или /. а) з 25 0,13; 6) 0,7; в) 0,6 іЗ Среднее арифметическое двух чисел равно 5,5. Одно число равно 3,7. Найди другое число. Найди значение дробного выражения: 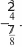 а) 2,84,25,1 6) а) 2,84,25,1 6)120 3 5,6 Скорость катера по течению реки равна 30,5 км/ч, а против течения — 27,5 км/ч. Какое расстояние катер пройдет по озеру за 1,6 часа? УPOK 29. АНАЛИЗ КОНТРОЛЬНОЙ РАБОТЫ №2 § 4. Отношения 14 часов, задания 172-245 В результате изучения темы ученики усвоят смысл по- нятий ‹отношение», ‹масштаб», овладеют умением записы- вать отношение величин, научатся упрощать отношения, записывать отношения в процентах, а также использовать понятие «отношение› для решения практических задач. В процессе работы над темой ‹Отношения» шестикласс- ники, с одной стороны, уточняют, повторяют и обобщают ранее изученный материал, активно используя его для усво- ения нового понятия. С другой стороны, углубляются и рас- ширяются знания, имеющиеся у школьников, они овладе- вают новой терминологией и новыми способами решения математических задач. УPOK 30. ЗАДАНИЯ 172-177 Ifenь. Рассмотреть понятие ‹отношение›, опираясь на ра- нее изученный материал 1-5 классов. Рекомендуем начать урок с задания №172, которое все уче- ники 6 класса могут выполнить самостоятельно, так как пред- лагаемые в нём вопросы доступны и понятны большинству ребят. Возможен и другой вариант начала урока. На доске записан текст задачи: «Петя собрал грибов в 3 раза больше, чем Коля. Сколько грибов собрал каждый, если вместе они собрали 80 грибов?» Учитель предлагает детям нарисовать схему, соответству- ющую данной задаче, и наблюдает за их работой. Затем вызывает нескольких учеников, которые справи- лись с заданием, и они изображают на доске схемы:    80 г.  Во сколько раз у Пети грибов больше, чем у Коли? (3 : 1) Какую часть грибы Коли составляют от грибов Пети? (1 3) Какую часть грибы Пети составляют от всех грибов? (3 : 4) Какую часть грибы Коли составляют от всех грибов? (1 : 4) Отвечая на эти вопросы, учащиеся пользуются любой из схем, которые изображены на доске. Записи 3 : 1, 1 : 3, 3 : 4, 1 : 4 также выносятся на доску. Теперь можно прочитать определение в учебнике на с. 38 и переформулировать при- ведённые выше вопросы, используя понятие ‹отношение». Приём переформулировки заданий и вопросов имеет боль- шое значение для понимания и усвоения этого понятия. Ва- рианты новых формулировок могут быть различными (в во- просительной или повелительной форме). Объясняя смысл того или иного отношения, шестикласс- ники используют уже знакомые им понятия. Например, в №173, измерив длину каждого отрезка, уче- ники объясняют, что отношение 11 5 показывает, во сколько раз длина отрезка MC больше длины отрезка CD, а отноше— ние 2 : 11 показывает, какую часть длина отрезка AB состав- ляет от длины отрезка MC. Запись отношений в виде дроби в задании № 173 помо- жет учащимся самостоятельно выписать пары взаимно об- ратных отношений. Прочитав текст №175, ребята анализируют записи Миши и Маши и выясняют, кто допустил ошибку и в чём её при- чина. Ответы сначала рассматриваются в пapax, а затем вы- носятся на фронтальное обсуждение. (Ошибка Миши в том, что он записал отношение величин, выраженных в единицах разных наименований.) Для работы с № 176 советуем вырезать из плотной бу- маги модели всех фигур и соответствующий каждой из них ЬAOB. Приступая к выполнению задания, ученики анали- зируют рисунки, и выбирают те из них, для которых можно записать отношение площади ЬAOBк площади всей фигуры. Для проверки ответов используются демонстрационные мо— дели фигур и соответствующий им ЬAOB. № 177. Шестиклассники читают задание и устно выпол- няют пункт а) (1 см от 5 см составляет i 5 |
