матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb. Скачать 2.01 Mb.
|
ЧЕТВЕРТЬ 50 часов § 13. Сравнение рациональных чисел 6 часов, задания 464-515 В результате изучения темы учащиеся угочнят имеющие- ся у них представления о рациональных числах, о координат- ной прямой, о модуле числа; усвоят правило сравнения отри- цательньіх чисел и приобретуг опыт сравнения рациональных чисел. УPOK 1. ЗАДАНИЯ 464-470 Іfель. Уточнить представления учащихся о рациональ- ных числах и о расположении точек с заданными коорди- натами на координатной прямой. Сформулировать правило сравнения отрицательных чисел. №464 выполняется устно. Одни пары чисел ученики мо- гут сравнить с помощью ранее усвоенных знаний, другие — с помощью координатной прямой, которая дана в учебнике. Например, сравнивая числа в пape 3,87 и 5 , они отмеча- ют, что число 3,87 содержит целую часть, и если его запи- сать в виде обыкновенной дроби, то это будет неправильная дробь, а дробь правильная. А любая неправильная дробь больше, чем любая правильная. Возможно и другое обоснование: достаточно сравнить це- лые части данных дробей. Сравнивая числа в пункте д), можно воспользоваться ко- ординатной прямой, где точка, которая находится правее, соответствует большему числу. Дети усвоили это правило, работая ещё с координатным лучом, поэтому для большин- ства оно является основным ориентиром. Пользуясь этим правилом, ученики самостоятельно вы- полняют в тетрадях №465, анализируя расположение точек на координатной прямой, которая дана в учебнике. №466 советуем обсудить фронтально, изобразив на доске координатные прямые с отмеченными точками. Например: 2 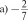 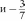  7 72 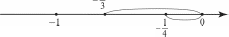  l l2 —4 l 2  И —3 3 И —3 34 При этом следует отметить дугой расстояние от данной точки до начала отсчёта, показав тем самым модуль каждого числа. Зная, что точка, которая находится на координатной пря- мой правее, соответствует большему числу, ученики смогут самостоятельно выполнить сравнение данных чисел: 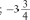 7 7 19 15 4 3 :> —4 7 7 19 15 4 3 :> —4 Сравнив модули чисел в каждой паре, они делают вывод, что модуль большего отрицательного числа меньше модуля меньшего отрицательного числа. В №467 во всех парах даны отрицательные числа, кото- рые легко сравнить, ориентируясь на их целые части. Советуем не торопиться с формулировкой правила срав- нения отрицательных чисел. Важно, чтобы ученики сами сделали вывод не только о расположении точек, соответству- ющих данным числам на координатной прямой, но и об изо— бражении на ней модулей этих чисел. Тогда при выполнении № 468—470 шестиклассники бу- дут пользоваться правилом сравнения отрицательных чисел с ориентировкой на понятие ‹модуль». (Меньшему отрица- тельному числу соответствует больший модуль). На дом: №470. УPOK 2. ЗАДАНИЯ 471-477 Lfeль. Создать дидактические условия для усвоения пра- вила сравнения отрицательных чисел. Продолжить форми- рование умения сравнивать рациональные числа. Советуем внимательно отнестись к №471, при выпол- нении которого учащиеся не только усваивают новый мате- риал, но и повторяют (уточняют) ранее изученные понятия. Например, в пункте а) необходимо уточнить, какие числа на- зывают рациональными. Тогда для доказательства того, что данное утверждение неверное, достаточно привести пример, в котором сравниваются два отрицательных числа (—9 —1), где модуль меньшего числа больше модуля большего числа. Таким же способом доказательства можно воспользовать- ся в пункте 6), где утверждение тоже неверное. Для доказа- тельства утверждения в пункте в) можно изобразить коорди- натную прямую, где будет видно, что любое положительное число расположено на ней правее нуля. 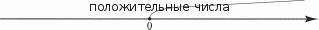 Аналогично можно доказать, что утверждение г) верное. 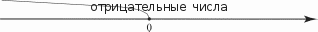 В пункте д) следует отметить, что модуль положительного числа равен этому числу. А то, что утверждение е) неверное, также можно доказать с помощью координатной прямой. ВЯ  №472 (устно): а) 1; 6) —1; в) назвать нельзя; г) назвать нельзя, так как координатную прямую можно продолжить влево и вправо до бесконечности. Рекомендуем предложить №473 для самостоятель- ной работы в парах. Учащиеся выбирают ту координатную прямую, которая соответствует данному условию. Правиль- ное выполнение задания будет свидетельствовать о понима- нии учениками изучаемых вопросов. Результаты самостоятельной работы обсуждаются фрон- тально с демонстрацией ответов на координатных прямых, которые учитель заранее изобразит на доске (верный ответ рисунки и ). №474 также позволяет проверить представления учащихся о положительных и отрицательных числах и о расположении точек с соответствующими координатами на координатной прямой. Задание выполняется учениками самостоятельно в тетрадях, затем проверяется фронтально с помощью коор- динатной прямой, изображённой на доске. Аналогично организуется деятельность класса при вы- полнении №475, 476 а), 6), в), 477 а), 6), в). На дом: №476 (r—e), 477 (r—e). УPOK 3. ЗАДАНИЯ 478-485 Іfель.Продолжить формирование умения сравнивать рациональные числа. После проверки домашнего задания учащиеся самостоя- тельно выполняют в тетрадях №478. №480 выполняется устно. Рассуждения учащихся иллю- стрируются на координатных прямых, заготовленных на доске.  а), г) а), г)—3 —2 —1 0 1 2 3 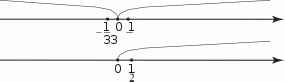 №482 сначала обсуждается фронтально с выполнением записей двойных неравенств на доске. Например, пункт а): Можно интерпретировать запись двойного неравенства и показать на координатной прямой. —2 —1 1 0 1 2 3 3,2 4 2 Пункт 6) учащиеся самостоятельно выполняют в тетра- дях. Если возникают трудности, они обращаются к коорди- натной прямой. №483 — самостоятельная работа в тетрадях. Для провер- ки полученных результатов можно использовать координат- ные прямые. мером: — рациональное число. При х = неравенство Утверждение 6) верное, так как модуль любого числа есть число положительное. На дом: №479, 481. УPOK 4. ЗАДАНИЯ 486-492 Ifenь.Сформировать у учащихся умение сравнивать мо- дули рациональных чисел. С №486 ученики работают сами, без помощи учителя. Правильными будут ответы а) — все данные числа целые, 7 И — положи- 8 не являются дробными; ответ 6) не подходит, т. к. числа 3 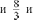 7 7не являются целыми. Поэтому возможен только один ответ: г) рациональные числа. №488 обсуждается фронтально. Ответы: можно на- звать: а) целым числом, так как в виде дроби записано число —5; 6) целым отрицательным; д) рациональным. Ответы в) и г) — не подходят. №489 (а,в, д) выполняется в тетрадях самостоятельно, а при проверке используется координатная прямая. Отве- ты ученики записывают в тетрадях в виде двойного нера- венства. Это могут быть разные числа. Например, в записи число 0: —1 0 3; 2 число натуральное 1 или 2: —1 1 3; —1 2 3; 2 число дробное положительное: —1 11 з. Так как в задании требуется записать только одно нера- венство, то в результате самостоятельной работы вариантов правильных ответов окажется много. Поэтому при проверке учитель может задать детям такие вопросы: Кто вставил в запись —1 .. 3 число 0? Дробное положительное число? (Ученики называют число.) У кого другие дробные положительные числа? Кто вставил натуральное число? Дробное отрицательное число? И т. д. Аналогично следует организовать работу и с №490. Пусть шестиклассники напишут самостоятельно в тетра- дях все целые отрицательные значения п, при которых вы- полняется неравенство а 4. Приступая к проверке самостоятельной работы, учитель сначала выясняет, сколько чисел записали дети. Должно быть записано три целых отрицательных числа —1; —2; —3. Ответ можно проверить на координатной прямой.  На дом: №491, 492. УРОКИ 5, 6. ЗАДАНИЯ 493-515 Lfeль. Создать дидактические условия для приобретения учащимися опыта в сравнении рациональных чисел; повто- рить ранее изученные понятия: ‹модуль числа», «противопо- ложные числа». После проверки домашнего задания ребята выполняют №493 самостоятельно в тетради. В пункте 6) они могут либо расположить модули чисел в порядке возрастания, либо сначала заменить каждый модуль положительным числом. Тогда в пунктах 6) и в) будут записаны одинаковые числа. №494 также выполняется самостоятельно. Если будут об- наружены ошибки, целесообразно предложитьдетям найти точ— ки, соответствующие данным числам на координатной прямой. №495, 496 могут вызвать у некоторых учеников затруд- нения, если не была проведена достаточная работа на ко- ординатной прямой. В этом случае учащиеся не имеют на- глядного представления о модуле числа и в связи с этим не осознают, что модуль любого числа есть число положитель- ное. Если же они усвоили это, то пункты а), 6) в №495 не должны оказаться сложными. Утверждения а) и г) — верные. Утверждение 6) — неверное. Для обоснования доста- точно воспользоваться примером 2 —7, но |2| |—7|. Утверждение д) также неверное. Для обоснования от- вета достаточно сравнить положительные числа: если 2 6, то |2| |6|. Утверждение в) — неверное. Здесь нужно сравнить от- рицательные числа, если —7 —5, то |—7| |—5|. Утверждение е) — неверное. Для этого достаточно сравнить положительное и отрицательное числа: если 5 3, то |5| |—З|. Аналогично обосновываются утверждения в №496: а) для любых рациональных чисел это утверждение не- верное, так как если |3| = |—З|, то утверждение 3 = —3 — не- верное, верным является утверждение 3 —3; 6) неверное, так как если | —5| |3|, то —5 3 (утвержде- ние —5 3 — неверное); в) неверное, так как если |—З| |—5|, то —3 —5. Работу с №496 советуем продолжить, выяснив, для ка- ких рациональных чисел могут выполняться утверждения а)—в). №497 (а,6) — для самостоятельной работы в тетрадях. При проверке пункта а) учитель выясняет: Какое первое число записали в ряду? (4,8) Есть ли другие положительные числа в ряду? (3,2 и 2,7) Какое из этих чисел больше? (3,2) Какое самое маленькое отрицательное число дано в ряду? (—8,1) Самое большое отрицательное число? (—1,5) Аналогично проверяется выполнение пункта 6). №498, №499 — для самостоятельной работы в тетра- дях. При проверке №498 ученики повторяют определение противоположного числа. В №499 школьники подбирают корень уравнения и про- веряют полученное равенство. Например: а) —х = 8; —(—8) = 8; х = —8; 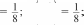 6) — = 12,5; —(—12,5) = 12,5; = —12,5; 6) — = 12,5; —(—12,5) = 12,5; = —12,5;в) —п После прочтения №500 ученики изображают в тетра- дях координатную прямую и отмечают на ней точки, соот- ветствующие числам (единичный отрезок каждый ученик выбирает сам) —4,5; —1,5; 3. Затем на этой же координатной прямой ребята отмечают точки, которые удалены от данных на 2 единицы, и записывают их координаты (должно быть 6 точек). —7 —6 —5 —4 —3 —2 —1 0 1 2 3 4 5 6 Учитель наблюдает за работой шестиклассников, оказы- вая индивидуальную помощь. На доску выносится коорди- натная прямая с точками A{—1,$);B(—4,5); С(3). Точки, отстоящие от каждой данной на 2 единицы, также отмечаются на координатной прямой. Для активизации дея- тельности учащихся советуем к доске приглашать учеников, которые не до конца справились с заданием (например, в их тетради отмечена только одна точка). Обозначать получившиеся точки, координаты которых удовлетворяют условию, будем теми же буквами с индексом. Учитель знакомит шестиклассников с такой записью, напри- мер: B,(—6,5) и 32 (—2,5); Л1(—3,5) и Л2(0,5); C1(1) и C2(5). №501. Пункты а), 6), в) выполняются самостоятельно. При фронтальной проверке дети называют результат и фор- мулируют определение модуля. №502. Ученики записывают в тетрадях по 3 числа к каждому пункту. При проверке отмечают на координатной прямой, изображённой учителем на доске, точки, соответ- ствующие выбранным числам. №504. Рекомендуем сначала записать в виде обыкно- венных дробей целые положительные числа. Проверяя рабо- ту, полезно обратить внимание детей на то, что в числителе должно быть записано число, кратное знаменателю. Действуя по аналогии, шестиклассники обычно справляются само- стоятельно и с записью целых отрицательных чисел в виде обыкновенных дробей. Тем не менее, на данном этапе обу- чения советуем акцентировать их внимание на записи знака «минус» перед дробью Результаты работы с №505 (а) и №506 (а) проверяются устно. В №506 (а) следует учесть, что в соответствии с тре- бованием задания учащиеся сначала записывают: а) данные числа в порядке убывания (8,7; 1; 0; —*; —1,4; —3,4). В этом случае они используют имеющиеся у них пред- ставления о расположении чисел на координатной прямой; 6) модули этих чисел в порядке убывания. В этом случае запись ряда чисел будет такой: |8|, |7|, |—3,4|, |—1,4|, |1|, ; |0|. В №508 советуем записать двойное неравенство —6 х 3, а затем ряд целых чисел, которые ему удовлетворяют (—5, —4, —3, —2, —1, 0, 1, 2). Полезно задать вопросы: Сколько целых чисел нужно записать? (8) Сколько из них целых отрицательных? (5) Сколько целых положительных? (2) На дом: №513 (r—e), 507. На б-м уроке деятельность учащихся при выполнении №509-515 организуется так же, как на предыдущем уроке. На дом: №513 (r—e), 515 (ж—м). |
