матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb.
|
|
УPOK 18. ЗАДАНИЯ 346-349, 351, 352 Lfeль. Сформировать умение вычислять длину окружно- сти, пользуясь формулой. Для формирования данного умения в учебнике пред- ложены задания, на выполнение которых отводится два урока. №346 целесообразно выполнить в классе. Сначала уча- щиеся самостоятельно его читают, затем знакомятся с рас- суждениями Миши и Маши и, выбрав любой из двух спосо- бов, отвечают на вопросы задачи. Результаты самостоятельной работы обсуждаются фронтально. Следует иметь в виду, что ребята могут подойти к решению задачи формально, ориен- тируясь только на числовые данные, то есть выполнив дей- ствие 15,6 : 5,2, они получат 3. Отсюда следует ответ: длина одной окружности в 3 раза больше длины другой окруж- носТИ. Чтобы ученики поняли, как решить задачу в одно дей- ствие, следует выполнить записи: 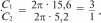 CC = 2 15,6; C2 = 2 5,2;Значит, длина большей окружности относится к длине меньшей окружности как 3 1, то есть длина большей окруж- ности в 3 раза больше, чем длина меньшей окружности. Полезно обсудить другую формулировку ответа: дли-  на меньшей окружности составляет 1 ОТ длины большей окружности. В результате работы с №346 дети осознают, что отношение длин окружностей равно отношению их радиу-сов 532 1 15,6 3 В этом случае решение последующих задач не вызовет у них затруднений. Таким образом, в результате решения данной задачи учащиеся не только усваивают новый материал, но и повто- ряют ранее изученные вопросы: сокращение дробей и отно- шения. Желательно рассмотреть в классе и задачу №347. Мно- гие смогут решить её устно, воспользовавшись рассуждени- ями Миши из предыдущей задачи и учитывая отношение 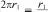 длин окружностей: 2 Г2 Г2Поэтому следует предоставить такую возможность всем шестиклассникам. Пусть они прочитают задачу самостоя- тельно, решат её устно и напишут в тетрадях только ответы (25 см, 5 см). При фронтальном обсуждении полученных ответов реко- мендуем выполнить на доске запись 2кгі п 2ftГ2 2 и нарисовать схему, обозначив отрезком ABдлину радиуса одной окруж- ности, а отрезком BC — длину радиуса другой окружности. 30 см  АВС Решение задачи №348 учащиеся записывают в тетрадях самостоятельно. Задачу №349 (а) советуем рассмотреть в классе. №349 (6, в) можно включить в домашнюю работу.  Рекомендуем в №349 (а) дополнительно к рисунку в учеб- нике использовать либо лист бумаги, который можно свер- нуть в трубку и показать на нём 0,8 см, предназначенные для сварного соединения, либо нарисовать на доске схематиче- ский рисунок этого листа. При оформлении решения учащиеся записывают сначала формулу длины окружности dC = п d), а затем выполняют вычисления: 1) С—3,14 3,8 = 11,932 (см); 2) 11,932 + 0,8 = 12,732 (см). Учитель предлагает округлить ответ до целых, до деся- тых, а также выразить его в миллиметрах. Дополнительно можно вычислить площадь и периметр этого листа. Задачи №351, 352 также следует обсудить в классе. Что- бы дети представили (No 351), что один оборот (вала, колеса) равен длине окружности, советуем воспользоваться рисун- ком из №344, приведённым в учебнике на с. 79, где Миша и Маша обсуждают один из способов измерения длины ОК]Э ЖНОСТИ. До записи решения задачи №351 можно обсудить план её решения: сначала вычислим, на какую глубину опускает- ся ведро при одном обороте вала, а затем ответим на вопрос задачи. После этого ученики записывают решение задачи са- мостоятельно. На доску выносятся только ответы к каждому действию. №352. Учащиеся самостоятельно записывают её реше- ние в тетрадях, выписывают на доску полученные ответы (они могут быть как верными, так и неверными). В процессе фронтального обсуждения выбирается верный ответ на во— прос задачи. При этом следует выразить в других единицах скорости величину, полученную в ответе: 942 м/мин. Записи производятся на доске: 942 м/мин = 56 520 м/ч = 56,52 км/ч и поясняются (1 ч = = 60 мин, 1 км = 1000 м). На дом: №349 (6, в). УPOK 19. ЗАДАНИЯ 353-356 Ifenь. Сформировать умение вычислять длину окружно- сти, пользуясь формулой. После проверки домашнего задания рекомендуем вы- полнить №353. Деятельность учащихся организуется так же как при выполнении №349. №354, 355 для самостоятельной работы по вариантам с последующей взаимной проверкой в парах. При выполнении задания №356 советуем вынести ри- сунок на доску, обозначить отмеченные точки буквами, рас- смотреть различные способы решения задачи. На дом: N354, 355 (другой вариант). УPOK 20. ЗАДАНИЯ 357-362 Ifenь. Познакомить шестиклассников с формулой пло- щади круга. Для знакомства учащихся с формулой площади круга ре- комендуем ориентироваться на №357, работу можно орга- низовать по-разному. 1-й вариант. Учитель показывает детям демонстраци- онные круги, которые разделены на 8, на 12, на 18, на 36 равных частей (секторов), и предлагает догадаться: как, разделив круг на равные секторы, измерить его площадь? Возможно, от детей поступят интересные предложения. Если их не будет, то можно обратиться к чтению рассуждений Миши и Маши, которые приведены в учебнике на с. 83. Од- нако восприятие нарисованной в учебнике фигуры, которая по форме напоминает прямоугольник, требует определённо- го уровня пространственного мышления. Поэтому, выбирая данный вариант работы с заданием №357, педагогу необхо- димо учитывать этот факт. 2-й вариант. Как показывает практика, возможен более доступный вариант работы с этим заданием. Он вызывает интерес у всего класса, так как связан с практической рабо- ТОй. Каждый ученик получает лист белой бумаги, на котором с помощью циркуля проводит окружность г —5 см. С помощью угольника дети делят круг сначала на 4 равные части, потом с помощью транспортира — на 8 равных частей. 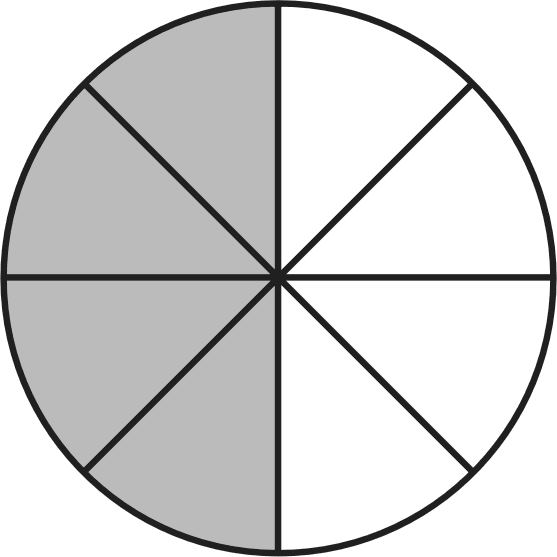 Затем ребята вырезают круг и разрешают его на 8 равных частей (секторов). Учитель предлагает каждому разложить пе- ред собой на парте эти фрагменты так, как показано на ри- сунке (рисунок нужно заранее заготовить). 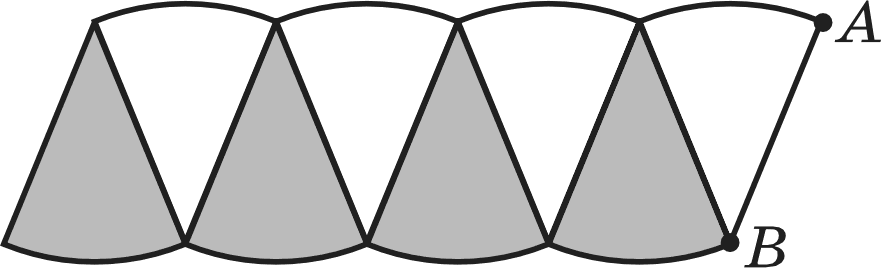 Педагог обращается к классу: — Как вы думаете, верно ли утверждение, что площадь круга равна площади данной фигуры? (Фигура состоит из тех же секторов, что и круг. Значит, площадь данной фигуры и площадь круга одинаковы.) Покажите на этой фигуре отрезок, длина которого равна радиусу круга. {AB) Покажите на рисунке линию, которая равна дли- не данной окружности. (Учащиеся показывают дуги внизу и наверху.) Запишите формулу длины окружности. {С—2пг) А чему равна длина четырёх дуг, которые расположены внизу? (or) Конечно, — подводит итог учитель, — фигура, изобра- жённая на рисунке, не очень похожа на прямоугольник. Но если мы разделим круг не на 8, а на 36 частей, то получим фигуру, которая дана в учебнике на с. 79. Она похожа на пря- моугольник? (Шестиклассники отвечают.) Чему равна длина этого прямоугольника? (or) Чему равна его ширина? (г) Верно ли утверждение, что площадь круга приближён- но равна площади прямоугольника? Найдите площадь прямоугольника. {S—rrг=пг2) Какой можно сделать вывод? {S—пг2 — формула пло- щади круга). Затем можно прочитать рассуждения Миши и Маши в учебнике. Для работы с заданием №358 приведённая в нём табли- ца выносится на доску, и учащиеся заполняют её.
Анализ таблицы позволяет сделать вывод о том, что дли- на окружности и её радиус являются прямо пропорциональ- ными величинами. Площадь круга и его радиус нельзя отнести ни к прямо пропорциональным величинам, ни к обратно пропорцио- нальным величинам. Желательно №359 обсудить на уроке и выяснить, какие измерения нужно выполнить, чтобы най- ти площадь каждой закрашенной фигуры. При этом условии  №359 можно включить в домашнюю работу.При выполнении №361 желательно предоставить всем детям возможность решить задачу устно, то есть отвести время (3-5 минут) на самостоятельное чтение задачи и на её обдумывание. Решившие задачу выходят к доске и записывают свои ответы. Они могут быть все одинаковыми, но могут быть и различными, например, для данной задачи такими: 1) 1 4; 2) 0,25; 3) . Учитель может привлечь к объяснению каждой записи того ученика, который её выполнил. Но возможен и другой вариант, когда к обсуждению привлекаются те дети, которые не справились с устным решением задачи. В этом случае учителю необходимо продумать последова— тельность тех вопросов и заданий, с которыми он будет об- ращаться к классу. Например: Запишите в виде буквенного выражения площадь кру- га радиусом 3,6 см. (п (3,6)2 см2) Найдите радиус меньшего круга. (3,6 : 2 = 1,8 см) Запишите в виде буквенного выражения площадь кру- га радиусом 1,8 см. (п (1,8)2 см2). Запишите отношение площади меньшего круга к пло- щади большего круга. (п (1,8)2 : п (3,6)2).  Представьте это отношение в виде дроби (1,8)2(3,6)2 Выполните сокращение. Если возникнут трудности, можно использовать такую запись: 3,141,81,8 _ 1 3,14 3,6 3,6 4 На дом: №360, 362. УPOK 21. ЗАДАНИЯ 363-369 Іfель. Формировать умение читать и строить круговые диаграммы. Для решения задачи №363 рекомендуем воспользовать- ся схемой, которую следует заранее заготовить на доске в та- ком виде:  После того как дети прочитают задачу, учитель предлагает обозначить на схеме центры окружностей, радиусы: гу,гу,г , а также известные в задаче величины. В результате проделанной работы имеем: 12 м 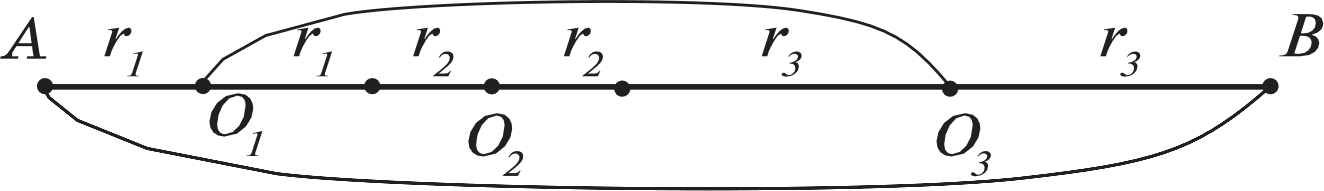 20 м Пользуясь схемой, учащиеся смогут самостоятельно ре- шить задачу: найдут сумму длин радиусов (r1 + гЗ). Она равна 20 — 12 = 8 (м); затем диаметр окружности с центром в точке O2 : 12 — 8 = 4 (м) и её радиус: 4 : 2 = 2 (м). Воспользовавшись формулой С — иd,дети вычислят длину этой окружности (С = п 4 (м)). Затем, используя фор- мулу S — п r2, найдут площадь круга, который ограничен этой окружностью {S — г4 (м2)). Заменив п его значением 3,14, выполнят вычисления. Полезно задать ученикам вопрос—‹ловушку»: ‹Получа- ется, что длина окружности п - 4 равна площади круга п - 4. Разве это возможно?» Некоторые дети попадаются в «ловушку», другие отмеча- ют, что в одном случае: rr(м) речь идёт о единицах длины, а в другом: ur (м2) — о единицах площади. При выполнении №364 прежде всего следует выяснить, какие измерения необходимо провести. Ни у кого из учени- ков не вызывает сомнений, что надо измерить радиус окруж- ности. Зная радиус, можно вычислить площадь круга. Для ЭТОГО Н ЖНО COCT£tBИTЬ П]ЭОПО]ЭЦИЮl 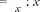 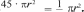 360 пг245 360 8 После выполнения №364 рекомендуем прочитать ин- формацию в рамочке и обсудить рисунок к №365. Вопросы для обсуждения: На сколько секторов разделён данный круг? (На три.) Чем ограничен кaждый сектор? (Двумя радиусами и дугой окружности.) Чем отличаются секторы друг от друга? (Углом между радиусами и длиной дуги.) Какова величина угла между радиусами меньшего по площади сектора? (30°) Какова величина угла между радиусами самого боль- шого по площади сектора? (360° — (70° + 30°) = 260°) С таким углом учащиеся встречаются впервые, поэтому учителю желательно прокомментировать ответы шестиклас— сников, если таковые будут. Если же дети не смогут ответить на этот вопрос, то учитель предложит им свою запись на доске с таким комментарием: Весь круг содержит 360°, поэтому для ответа на во- прос надо провести вычисления: 360° — 70° — 30° = 260°. Оказывается, можно говорить об углах, которые больше раз- вёрнутого. Если нарисовать круг и провести в нём диаметр, то хорошо видно, что круг содержит два развёрнутых угла, то есть 360°. 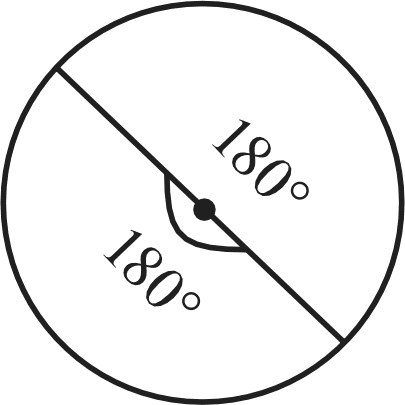 (Рисунок можно заготовить на доске заранее либо выпол- нять его по ходу рассуждений.) Теперь можно прочитать задачу №365 и обсудить план её решения. В случае затруднений советуем направлять деятельность учащихся такими вопросами: Как обозначен на диаграмме весь маршрут длиною в 180 км? (Кругом.)  Если круг содержит 360°, то можно ли ответить на во- прос: сколько километров содержит сектор, между радиуса- ми которого 1°? 180 : 360 = i 2Какое расстояние туристы прошли пешком? 30 = 15 (км). Проехали на поезде? i  270 = 35 (км). Проехали на автобусе? 180 — 15 — 35 = = 130 (км). 260 = 130 (км) или Можно ли решить эту задачу, составив пропорцию? (Да.) Как записать условие задачи кратко, чтобы составить 360° — 180 км; 70° — х км. Какая зависимость между величиной угла и длиной пути? (Прямо пропорциональная.) Учащиеся записывают пропорцию и, пользуясь основным свойством пропорции, находят неизвестное: 360 180 18070 70 х ' 360 ' = 35 (км). Аналогично находится расстояние, которое туристы прошли пешком и проехали на поезде. Задачу №366 советуем предварительно обсудить фрон- тально и наметить план её решения. Сначала узнаем длину туристического маршрута. Найдём величину угла между радиусами сектора, ко- торый обозначает 1 км. Начертим круг. Разделим его на секторы. Выполнив вычисления: 170 + 30 + 60 + 100, получаем 360 км. Значит, сектор, в котором величина угла между ра- диусами равна 1°, обозначает 1 км. Дети чертят окружность и, пользуясь транспортиром, строят соответствующие углы: 170°, 30°, 60°, 100°. Аналогичные рассуждения проводятся при решении за- дачи №367. На дом: №368, 369. УPOK 22. ЗАДАНИЯ 370-376 Іfель. Формировать умение пользоваться формулами длины окружности и площади круга при вычислении пло- щади сектора. Задачу №373 следует обсудить в классе на этом или на следующем уроке. При подсчёте дней следует иметь в виду, что в марте 31 день. Значит, надо из 31 вычесть 4 дня (1, 2, 3 и 4 марта), а потом добавить три дня апреля (1, 2, 3 апреля). Затем узнать количество дней до 18 апреля (30 + 15). На основе полученных данных осуществляется краткая запись: 720 р. — 30 д.; х р. — 45 д. При составлении пропорции следует иметь в виду, что зависимость между данными величинами обратно пропор- циональная. Поэтому отношение одних величин равно об- ратному отношению других величин: Теперь можно ответить на вопрос задачи: 720 — 480 = 240 (р.) УРОКИ 23, 24. ЗАДАНИЯ 377-390 Іfель. Совершенствовать умения решать задачи с пропор- циональными величинами и процентами. На этих уроках учащиеся самостоятельно решают задачи с последующей фронтальной проверкой или взаимной про- веркой в парах. Последовательность решаемых задач опреде- ляет учитель по своему усмотрению. №377, 379, 382, 383 и 385 — это задачи с пропорци- ональными величинами. Решение таких задач подробно рассматривалось в § 6 Формулы. Прямая и обратная про- порциональные зависимости. Если учащиеся затруднятся с решением, советуем предложить им вернуться к задаче №300 на с. 66 и рассмотреть рассуждения Миши и Маши. №384 — это практическая задача, важно понимать, что ответ должен быть целым числом и округление при закупке строительных материалов производится в большую› сторону. №386, 387 и 388 (а) — это задачи с процентами. При не- обходимости, если у учащихся возникнут затруднения в ре- шении этих задач, рекомендуем предложить им воспользо— ваться краткой записью, представленной в №306 на с. 68. №378, 380 и 381 — это задачи с обратной пропорцио- нальной зависимостью величин. Рекомендуем решить их по действиям с комментариями. Например, решение задачи №378 можно оформить так: 15 32 = 480 (6.) — всего банок сока; 15 + 5 = 20 (6.) — банок сока в одной новой коробке; 480 : 20 = 24 (к.) — понадобится новых коробок. №388 (6) и 389 рекомендуем для домашней работы. УPOK 25. КОНТРОЛЬНАЯ РАБОТА №4 Ifenь. Проверить усвоение понятий: ‹отношение›, «про- порция», ‹прямая пропорциональная зависимость», «обратная пропорциональная зависимость» и формул длины окружно- сти и площади круга. Примерное содержание контрольной работы №4 ВармантI Запиши отношения и упрости их: а) 20 см к 4 м; б) 9 м к 27 дм. Запиши отношение а к b и упрости его, если: а) а : 3,2 = b :0,4; 6) 6,8 : п = 0,2 : Ь. Начерти прямоугольник, у которого стороны относятся как 0,4 : 0,7. Реши задачу, составив пропорцию. а) Из 15 кг сливок получают 3,5 кг масла. Сколько кило- граммов сливок нужно взять, чтобы получить 7,7 кг масла? 6) Пешеход, скорость которого 4,5 км/ч, проходит расстоя- ние от города до деревни за 3 ч 15 мин. Сколько времени понадобится пешеходу, чтобы пройти это расстояние, если он увеличит свою скорость на 1,5 км/ч? Колесо диаметром 80 см, пройдя некоторое расстояние, сделало 120 оборотов. Найди это расстояние и запиши ответ приближённо в метрах. (Все вычисления выполни в тетради.) Радиус круга 6 см. Найди площадь этого круга и длину окружности, которая его ограничивает. (Все вычисле- ния выполни в тетради.) ВариантМ Запиши отношения и упрости их: а) 15 кг к 300 г; 6) 8 т к 16 ц. Запиши отношение а к b и упрости его, если: а) а : 9,5 = b : 0,5; 6) 7,2 : п = 0,8 : Ь. Начерти прямоугольник, у которого стороны относятся как 0,3 : 0,9. Реши задачу, составив пропорцию. а) Из 85 кг свёклы получено 12 кг caxapa. Сколько кило- граммов свёклы понадобится, чтобы получить 72 кг caxapa? 6) Машина, скорость которой 90 км/ч, проезжает рас- стояние между городами за 4 ч. Сколько времени понадобится машине, чтобы проехать это расстоя- ние, если её скорость уменьшится на 15 км/ч? Колесо радиусом 26 см, пройдя некоторое расстояние, сделало 140 оборотов. Найди это расстояние и запиши его приближённо в метрах. (Все вычисления выполни в тетради.) Диаметр круга 8 см. Найди площадь этого круга и длину окружности, которая его ограничивает. (Все вычисле- ния выполни в тетради.) УPOK 26. АНАЛИЗ КОНТРОЛЬНОЙ РАБОТЫ №4 | |||||||||||||||||||||||||||||||||||||||
