матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb.
|
ЧЕТВЕРТЬ 35 часов § 5. Пропорции 5 часов, задания 246-269 В результате изучения темы учащиеся усвоят определе- ние пропорции, её основное свойство, овладеют умением со- ставлять пропорции, использовать понятие ‹пропорция» при решении уравнений и арифметических задач. УРОКИ 1, 2. ЗАДАНИЯ 246-252 (а—в) Lfeль.Познакомить учащихся с определением понятия «пропорция» и основным свойством пропорции. Школьники подготовлены к восприятию определения пропорции в предшествующей теме «Отношения». Опираясь на ранее усвоенные знания и умения, они смогут самосто- ятельно выполнить №246. Рекомендуем выписать на доске отношения 1,5 : 2; 3 : 6; 4,5 : 8; 6 : 8; 15 : 10 и предложить уче- никам выбрать те пары отношений, из которых можно со- ставить верные равенства. Как только кто-то из детей выберет такую пару отно- шений, он записывает равенство на доске. Вполне возмож— но, что на доске появятся не одно, а два и даже три ра- венства, среди которых могут быть и неверные. Например, 6 : 8 = 15 : 10. В этом случае следует доказать, что данные от- ношения не равны. Это легко сделать, если записать каждое  отношение в виде дроби 658 10‘ Слева — правильная дробь, справа — неправильная, их равенство невозможно. Запись 3 : 6 = 6 : 8 также будет неверным равенством, в чём легко убедиться, сравнивая дроби —3 и —з . Эти дроби 6 4 не могут быть равными, так как у них одинаковые мислите- ли, но разные знаменатели. В результате обсуждения на доске остаётся одно равен- ство, которое можно записать либо в таком виде: 1,5 2 = 6 8, либо в таком: 135 6 2 8 После проведённой работы учащиеся открывают учебник на с. 52, знакомятся с рассуждениями Миши и Маши и ком- ментируют способы их действий. (Миша вычислил каждое отношение, а затем составил равенство из тех отношений, где получились одинаковые результаты. Маша записала каждое отношение в виде дроби и упростила его. Это позволило ей найти равные отношения. Итак, Миша записал ответ в та- ком виде: 1,5 2 6 8. Маша — в таком: 5 6 2 8 Затем ученики читают определение на с. 52. Вопрос ' для самостоятельного поиска информации из истории математики. №247. Для доказательства равенства двух отношений достаточно записать каждое из них в виде дроби и выпол- нить сокращение. Например: 15 3. 27 3 10 2’ 18 2 и т. д.  №248 желательно обсудить сначала в пapax, а за- тем проверить результаты этой работы. При обоснова- нии выбранных пар отношений ученики повторяют ра- нее изученные вопросы: правило записи смешанного числа в виде неправильной дроби; правило деления дро- бей; понятие обратной дроби и др. Например, в пункте 2) надо выполнить деление. Для этого смешанные чис- ла первого отношения записывают в виде неправильныхдробей: 2 32 Разделив на 7   2получают 3  Значит, 23 32 или 2 3, и из отношений пункта 2) мож-но составить пропорцию. В результате выполнения №249 шестиклассники заме- чают, что произведение крайних членов пропорции равно произведению её средних членов, и после этого знакомятся С ОСНОВНЫМ СВОЙСТВОМ ПЈЭОПО]ЭЦИИ. №251 на нахождение неизвестного члена пропорции. Учитель выписывает на доске равенство  закрыты) и предлагает детям решить уравнение.(учебники Как правило, учащиеся предлагают два способа, анало- гичных тем, которые выполнили Миша и Маша. Можно записать оба этих способа на доске. Если же будет предло- жен только один способ, советуем открыть учебники и про- комментировать записи Миши и Маши. Миша рассматри- вал неизвестный член пропорции как неизвестное делимое, которое равно частному, умноженному на делитель. Маша воспользовалась основным свойством пропорции и записа- ла равенство произведений крайних и средних членов. Затем решила уравнение, находя неизвестный множитель. На дом: №247 (ж—и), 248 (5, 6), 250, 252 (а—в). УPOK 3. ЗАДАНИЯ 252 (г—и)—254, 256-259 Іfель. Создать дидактические условия для усвоения ос- новного свойства пропорции и применения понятия «про- порция› для решения уравнений. После проверки домашнего задания ученики самостоя- тельно выполняют №252 (r—e), где нужно решить уравне- НИЯ, ПОЛЬЗ ЯСЬ ОСНОВНЫМ GBOЙGTBOM П]ЭОПО}ЭЦИИ. В №253 шестиклассникам предложено, не решая урав- нений, выбрать те, которые имеют одинаковые корни. Ребята обычно пользуются основным свойством пропорции и пред- ставляют х в виде дробных выражений, которые можно вы- писать на доске. Сравнение полученных дробных выраже- ний позволяет сделать вывод о том, какие уравнения имеют одинаковые корни. Одинаковые корни имеют уравнения а), 6), г). №254. Дети могут его выполнить сначала самостоятель- но, по вариантам. Например, 1-м вармант составляет про- порции в пунктах 1), 3), а Л-й вариант— 5), 7). Для получе- ния пропорций из данного отношения учащиеся пользуются правилом сокращения дроби или основным свойством дро- би. Дети могут рассуждать по—разному. Например, в пун- кте 1): 6,4 : 16 = 64 : 160 (для получения пропорции использо- вано основное свойство дроби). Полезно выполнить проверку, применив основное свойство пропорции: 6,4 160 = 1024; 16 64 = 1024. 6,4 : 16 = 0,4 : 1 (для получения пропорции данное от- ношение записали в виде дроби 6,4 16 и сократили её на 16); 6,4 : 16 = 1,6 : 4 (оба члена отношения уменьшили в 4 раза); 6,4 : 16 = 32 : 80 (оба члена отношения увеличили в 5 раз). №256 рекомендуем для парной работы. Ученики анали- зируют действия Миши и Маши и обсуждают ответ на во— прос задания. №257 — фронтально. Сравнив числитель и знаменатель 7  дроби 8 ученики отвечают на вопрос а). (Больше число Ь.)5 4 Для ответа на вопрос 6), они делят знаменатель на числитель: 54 3 7 2_1 _31 218 4_2 = 111 {bбольше а в 1 11 раз). 8 4 8 4 31 31 31 31 №258 (а, в) ребята выполняют самостоятельно в тетра- дях. Для того, чтобы подобрать значения а, они пользуют- ся основным свойством дроби. Для проверки составленной пропорции рекомендуем использовать основное свойство пропорции. Например:
 Получаем пропорцию: 0,5 1. 7,2 14,4’ п = 1; b—14,4; 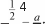   4 6 4 96 54 7 b7 7 1 7 7 7 7 12 12 12 а = 54; b —7. Рекомендуем проверять составленную пропорцию, ис- пользуя её основное свойство. №259 выполняется самостоятельно и затем проверяется фронтально.  На дом: №252 (ж—и), 254 (2, 4, 6, 8), 258 (б).УPOK 4. ЗАДАНИЯ 255, 260-263 Lfeль. Совершенствовать умение решать уравнения, ис- пользуя основное свойство пропорции. Научиться состав- лять новые пропорции из данной. Равенства, предложенные в №260, рекомендуем поместить на доску и обсудить, в чём их сходство и различие, а также до- казать, что каждое из них является пропорцией. Шестикласс- ники обычно отмечают, что числа в равенствах одни и те же. В равенстве а) поменяли местами средние члены, а в ра- венстве 6) переставили крайние члены пропорции. Для до- казательства того, что оба равенства являются пропорциями, учащиеся используют основное свойство пропорции и убеж- даются в том, что от перестановки средних или крайних членов пропорции получается равенство, которое также яв- ляется пропорцией (переместительное свойство умножения). После фронтального обсуждения рекомендуем прочитать диалог Миши и Маши и правило на с. 56 учебника. Затем дети записывают в тетрадь пропорцию 3 : 4 = 6 : 8 (No 261), и учитель предлагает им составить из этой пропор- ции новые, пользуясь правилом перестановки членов про- порции. В тетрадях появляются записи: 3 : 6 = 4 : 8; 8 : 4 = 6 : 3. Можно ли составить из данной пропорции ещё одну пропорцию? — спрашивает педагог. Возможно, кто—то из учеников предложит переставить одновременно и средние, и крайние члены пропорции и по- лучит пропорцию 8 : 6 = 4 : 3. Если такое предложение не поступит, учитель может сам записать на доске пропорцию 8 : 6 = 4 : 3 и обратиться к шестиклассникам с предложе- нием выяснить, как эта пропорция может быть получена из данной (3 : 4 = 6 : 8). Здесь необходимо обратить внима- ние на тот факт, что, переставляя одновременно и крайние, и средние члены пропорции, мы получаем слева и справа отношения, обратные отношениям данной пропорции. Советуем выписать эти пропорции на доску: 3 : 4 = 6 : 8 и 4 : 3 = 8 : 6. Если учитель выполнит рекомендации, данные к №261, то №262 не вызовет у детей затруднений, и они самостоятель- но запишут из пропорции b :а— 3 : 7 пропорцию п : b— 7 : 3, то есть найдут отношение а : Ь. Для выполнения №262 (6, в) нужно поменять местами средние члены пропорции: 6) а17 = b3; в) 13 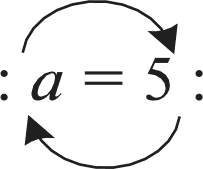 9‘а:b—17 : 3; 13 : 5 = а:Ь. Советуем также обратить внимание учащихся на то, что отношения, данные в любой пропорции, можно менять мес- тами, то есть пропорцию 13 : 5 = п : bможно записать так: п : b— 13 : 5. При работе с №263 важно верно составить первую про- порцию. Поэтому рекомендуем действовать поэтапно. Снача- ла ребята самостоятельно записывают в тетрадях одну про— порцию, пользуясь данными числами: 42, 18, 6 и 14. Затем выполняют преобразования с ней. Предложенные варианты выносятся на доску и обсуждаются. Большинство школьников обычно записывает пропорцию 42 : 14 = 18 : 6. Но возможны и другие варианты, а именно: 14 : 42 = 6 : 18; 14 : 6 = 42 : 18; 18 : 42 = 6 : 14. Пользуясь ос- НОВНЫМ GBOЙCTBOM П}ЭОПО{ЭЦИИ ИЛИ ВЫЧИСЛЯЯ ОТНОШ НИЯ, З£t- писанные слева и справа, учащиеся доказывают, что каждое из записанных равенств является пропорцией. Необходимо, чтобы дети поняли общий способ действия, то есть то, что с каждой предложенной пропорцией выполняют- ся одни и те же преобразования: 1) меняются местами средние члены пропорции; 2) меняются местами крайние члены пропор- ции; 3) данные в пропорции отношения заменяются обратными. На дом: №255. УPOK 5. ЗАДАНИЯ 264-269 Іfель.Формировать умение составлять пропорции на основе равенства произведений крайних и средних членов пропорции. После проверки домашнего задания учащиеся самостоя- тельно выполняют №264. Выбрав пропорции а) и 6), ше- стиклассники составляют из каждой ещё три пропорции. №265 вызывает у некоторых детей затруднения. Как правило, это связано с тем, что при составлении пропорций они пользуются вычислением отношений, а не основным свойством пропорции. Те ребята, которые ориентируются в крайних и средних чле- нах пропорции и усвоили основное свойство пропорции, без труда составляют из равенства 0,3 0,9 = 27 0,01 пропорцию 0,3 : 27 = 0,01 : 0,9, рассматривая 0,3 0,9 как произведение крайних членов, а 27 0,01 как произведение средних членов. Если же ученики рассматривают произведение 0,3 0,9 как произведение средних членов, а 27 0,01 как произведение край- них членов, то они составляют пропорцию 27 : 0,3 = 0,9 : 0,01. Рекомендуем обсудить с классом «механизм» составления пропорции из данного равенства произведений и выполнить на доске такие записи: Если 0,3 0,9 — произведение крайних членов, то 0,3 : 0,01 = 27 : 0,9. Заполним ‹окошки», воспользовавшись произведени- ем средних членов 0,3 : 27 = 0,01 : 0,9. Теперь можно из данной пропорции составить ещё три: поменяв местами крайние члены пропорции; поменяв местами средние члены пропорции; заменив каждое отношение, данное в пропорции, об- ратным ему отношением. №266 целесообразно обсудить в классе. Текст №267 лучше вынести на доску, чтобы ученики по- пытались выполнить его самостоятельно, и только в случае за- труднений следует воспользоваться записями Миши и Маши. Работа с №268 а) организуется так же, как с №263. №269 (а,г) ученики выполняют самостоятельно. В за- висимости от результатов работы на доску выносятся либо только корни уравнений, либо запись решения уравнений и тех преобразований, которые были произведены с дробны- ми выражениями. На дом: №268 (6, в), 269 (6, в). § 6. Формулы. Прямая и обратная пропорциональные зависимости 7 часов, задания 270-321 В результате изучения темы учащиеся овладеют умени- ями: распознавать прямо пропорциональную и обратно про- порциональную зависимости, пользуясь их определениями, выражать зависимость между величинами в виде формул, применять знания о прямой и обратной пропорциональных зависимостях для составления пропорций, решать текстовые задачи арифметическим и алгебраическим способами. УPOK 6. ЗАДАНИЯ 270-275 Lfeль.Познакомить учащихся с понятием ‹формула› и определением прямо пропорциональных величин. Подготовительная работа к изучению данной темы осу- ществлялась как в начальной школе, так и в 5 классе: наблю- дение изменения одних величин в зависимости от изменения других, знакомство с буквенными выражениями, решение арифметических задач, запись с помощью буквенной симво- лики свойств действий сложения и умножения, вычисление площади прямоугольника, объёма куба и параллелепипеда. Большинство шестиклассников готовы к восприятию новых понятий, при усвоении которых они могут не толь- ко воспользоваться приобретённым ранее опытом, но и про- дуктивно повторять уже изученный материал, а также совер- шенствовать умения решать арифметические задачи. Для знакомства учащихся с формулами в учебнике пред- лагаются задачи, с которыми большинство школьников смогли бы справиться самостоятельно ещё в начальной шко- ле. Поэтому рекомендуем задачу №270 решить устно и за- писать полученные ответы в таблице на доске:
Подводя итог проделанной работы, учитель выясняет, как дети рассуждали, отвечая на вопросы задачи. К рассуждениям Миши и Маши, приведённым в учеб- нике, советуем обратиться только после того, как все жела- ющие шестиклассники выскажутся. Ответы могут быть как верными, так и неверными, полными и неполными. Одни будут рассуждать, как Миша, другие — как Маша. Возможна и такая ситуация, когда некоторые ребята не смо- гут объяснить выполняемых действий. В последнем случае целесообразно прочитать диалог Миши и Маши в учебни- ке. От правила, которым пользовалась Маша, легко перейти к формуле, обозначив буквами величины: цена (с), количе- ство {т), стоимость (С). С = с т.  Работу с №270 можно продолжить, составив обратные задачи, и записав к ним формулу: С = с - m в виде: с =m = С, а затем сформулировать эти же записи в виде правила. При обсуждении №270 полезно выяснить, какие вели- чины изменялись, а какие не изменялись (оставались посто— ЯННЫМИ). Задачу №271 рекомендуем обсудить в классе. После об- суждения ученики самостоятельно запишут формулу, а дома ответят на поставленные в задаче вопросы. Формулу к задаче №272 ученики записывают самосто- ятельно. На доску следует вынести как верные, так и невер- ные записи формул, и обсудить их. Проведённая работа даёт возможность ребятам выпол- нить самостоятельно №273. В зависимости от состава класса самостоятельную работу можно организовать по-разному: ь'’ й вариант. Учащиеся записывают в тетрадях решение задачи (её следует оформить в таблице), а затем формулу, ко- торой надо воспользоваться п s Желательно обратить внимание шестиклассников на то, что выбранная ими запись получена из формулы площади прямоугольника: S— аЬ. йвариант. Учащиеся выбирают в учебнике нужную формулу и обосновывают свой выбор. На следующем этапе урока шестиклассники знакомятся с определением прямо пропорциональной зависимости. Для проверки понимания смысла этого определения целесообразно предложить школьникам выбрать прямо пропорциональные величины из тех, которые приведены в №274. Обосновывая свой выбор, ученики обращаются к опре- делению. (Количество и стоимость при постоянной цене являются прямо пропорциональными величинами, так как если количество увеличить в несколько раз, то и стоимость увеличится во столько же раз.) Для конкретизации можно использовать таблицу, составленную в начале урока при вы- полнении №270.
Таблицей стоит воспользоваться и для конкретизации ут- верждения: «Отношения соответствующих значений стоимо- сти и количества равны постоянному числу». “ Т‘‘‘ С этой же целью выполняется №275. Ориентируясь на определение, шестиклассники самостоятельно анализируют таблицу. Учитель может написать на доске два ответа: ‹Да› и «Нет» и быстро выяснить мнения учащихся. Скорее всего, разно- гласий не будет и все выберут ответ «Да›. Однако для дости- жения цели задания важно, чтобы ученики обосновали свой выбор, ссылаясь на определение. Поэтому рекомендуем изо- бразить на доске схему, приведённую в учебнике, и запол- нить её коллективно. 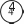  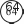 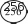     4 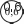 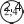      —Желательно, чтобы ученики, вызванные к доске, прого- варивали определение прямо пропорциональных величин и соотносили с ним те действия, которые выполнялись при анализе таблицы и заполнении схемы. В результате проделанной работы на доске появляется за- полненная схема, из которой хорошо видно, что при увели- чении одной величины в несколько раз другая увеличивается во столько же раз.  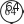 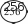       4 4 4 4 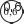 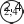    4 4 4 - 4  Т —Затем школьники проверяют, чему равны отношения со- ответствующих величин: 0,6 _ 2,4 _ 9,6 _ 38,4 153,6 1 4 16 64 256 |