матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb. Скачать 2.01 Mb.
|
=0,6Чтобы установить связь предыдущих тем (‹Отношения» и ‹Пропорция›) с новым материалом, рекомендуем, пользу- ясь таблицей, составить 3-4 пропорции. На дом: №271. УPOK 7. ЗАДАНИЯ 276-280 Іfель. Познакомить учащихся с определением обратно пропорциональных величин. После проверки домашней работы коллективно обсужда- ется №276. Текст: «За 4 м ткани заплатили 480 р., а за 6 м та- кой же ткани — 720 р.» советуем вынести на доску, чтобы уче- ники сначала самостоятельно, не пользуясь рассуждениями Миши и Маши, составили и записали в тетрадях пропорции. Поставленные детьми пропорции следует записать на до- ске и обсудить коллективно. Объясняя смысл полученных пропорций, необходимо учитывать ту реальную ситуацию, которая задействована в условии. Например, в ответах Миши и Маши имеется объ- яснение двух пропорций: 6 720 4 480 4 480 “ 6 720 Но шестиклассники могут предложить и другие вари- анты. Например: а) 480 720 4 6 Эта пропорция показывает, 4 6 что цена ткани — величина постоянная; 6) 480 720 Это равенство является пропорцией, но ученики испытывают за- труднения в объяснении её смысла с точки зрения ситуации, данной в условии. Хотя здесь можно говорить о том количе- стве метров, которые приходятся на 1 р. (это тоже величина постоянная). Подводя итог проделанной работе, учитель уточняет, что в условии есть постоянная величина (цена), и есть величи- ны, которые изменяются (количество и стоимость). Затем учащиеся читают определение обратно пропорци- ональной зависимости (с. 60) и, пользуясь определениями прямо пропорциональной и обратно пропорциональной за- висимостей, выполняют №277. Методика работы с №278 такая же, как и с №275. Ре- комендуем особое внимание уделить пункту 2), который связан с записью отношений. Советуем сначала прочитать правило, на которое следует ориентироваться при выпол- нении этого пункта: «Если величины обратно пропорци- ональны, то отношение значений одной величины равно обратному отношению соответствующих значений другой величины». Затем конкретизировать его, пользуясь табли- цей и предварительно уточнив, что следует понимать под обратным отношением. На дом: №279, 280. УPOK 8. ЗАДАНИЯ 281-287 Іfель. Формировать у шестиклассников умения: рас- познавать прямо пропорциональную и обратно пропорци- ональную зависимости, составлять пропорции, пользуясь определением прямо пропорциональных или обратно про- порциональных величин. После проверки домашнего задания учитель выносит на доску таблицу из №283. Учащиеся коллективно её запол- няют, повторяя взаимосвязь между величинами: скорость, время, расстояние. Делают вывод, что утверждение, сформу- лированное в задании, — неверное. Заметим, что при этом большая часть детей опирается на тот опыт, который они приобрели, решая задачи «на движение› в 4 и 5 классах. По- этому необходимо обосновать данное утверждение, исполь- зуя новое понятие, то есть обратиться к определению обрат- но пропорциональных величин. А это значит: проследить, как изменяется одна величина в зависимо- сти от изменения другой. Для этого можно воспользоваться схемой: 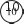 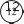 1,2 1,21 1 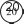  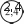 1 1 1 1 1 1 1 1убедиться в том, что произведение соответствующих значений величин (х и у) равно постоянному числу; убедиться в том, что отношение значений одной вели- чины равно обратному отношению значений другой величи- ны, то есть, пользуясь таблицей, составить пропорции. По- сле этого можно проанализировать ответы Миши и Маши и сделать вывод, что ошибку допустил Миша. Он непра- вильно определил зависимость между величинами. Таблица из №284 также выносится на доску и заполня- ется коллективно. Анализируя составленную таблицу с точки зрения определений прямо пропорциональной и обратно про- порциональной зависимостей, учащиеся делают вывод, что длина стороны квадрата и его площадь не являются ни прямо пропорциональными, ни обратно пропорциональными вели- чинами. Рекомендуем провести анализ таблицы по тому же плану, что и в №283, так как это будет способствовать пониманию и усвоению изучаемых вопросов. Аналогично анализируются таблицы, предложенные №285, 286. На дом: №281, 282, 287. УPOK 9. ЗАДАНИЯ 288-296 Іfель. Сформировать умение записывать прямо про- порциональную и обратно пропорциональную зависимости в виде формул. После проверки домашнего задания учащиеся самостоя- тельно выполняют №288, 291. При проверке результатов они обосновывают свои ответы, используя схему и определения пря- мо пропорциональных и обратно пропорциональных величин. Затем выполняются №292-296. Учащиеся устно отвечают на вопросы а) и 6) в каждом задании. Например, №292. ‹Пешеход за некоторое вре- мя прошёл 8 км. а) Какое расстояние он пройдёт за это же время, если увеличит скорость в 1,2 раза?». Ответ: ‹Пешеход пройдёт за это же время расстояние в 1,2 раза больше›. (Вы- числения выполняются устно: 8 1,2 = 9,6 (км). Аналогичные рассуждения даются в пункте 6).) После этого шестиклассники самостоятельно выбирают формулу, которой удобно воспользоваться для обоснования ответа (S— v f; здесь время — постоянная величина, а рас- стояние и скорость — величины прямо пропорциональные). На дом: №289, 290. УPOK 10. ЗАДАНИЯ 297-303, 305 Іfель. Формировать умение составлять пропорции при решении задач. Следует иметь в виду, что многие задачи учащиеся мо- гут решать арифметическим способом без составления пропорций. Этим можно воспользоваться для сравнения способов решения задач и для выбора из них рациональ- ного. Чтобы школьники усвоили приём составления про- порций, рекомендуем педагогу выполнять анализ задачи с точки зрения изменения представленных в ней величин (Во сколько раз увеличилась (уменьшилась) та или иная величина?). Такая работа поможет детям научиться опре- делять вид зависимости и решать задачи с помощью со— ставления пропорций. Текст №297 советуем вынести на доску и предложить шестиклассникам для самостоятельной работы. Практика показывает, что большинство учеников уверенно справля- ются с арифметическим способом решения (по действиям, как Маша). Способ решения Миши целесообразно вынести на доску и обсудить записи в каждом действии. В результате можно составить план, на который следует ориентироваться, решая текстовые задачи с помощью пропорции. Выполняем краткую запись. Определяем, какая зависимость существует между ве- ЛИЧИНБМИ. Составляем пропорцию. Преобразуем пропорцию, используя основное её свой- CTBO. Решаем уравнение. Текст задачи №300 также следует вынести на доску, чтобы учащиеся решили её самостоятельно. В случае затруд- нений они могут пользоваться планом (см. №297). После записи решения задачи можно прочитать в учебнике рас- суждения Миши и Маши. Задачу №301 ученики могут сначала решить арифмети- ческим способом устно, а в тетрадях записать её решение, используя пропорцию. При решении задачи ученики вспоминают определение масштаба и уточняют, что показы- вает запись 1 : 3000 000, затем выполняют краткую запись. Если возникают трудности, учитель оказывает помощь. Он пишет на доске: На карте На местности и направляет деятельность класса вопросами: Что запишем слева? Что запишем справа? На доске появляется краткая запись: 1 см — 3000 000 см; 9 см — х см. Затем определяется и обосновывается вид зависимости (прямо пропорциональная). Составляется пропорция, где буквой х обозначено расстояние на местности, которое на карте изображено отрезком в 9 см. Решается уравнение. №302 целесообразно решить арифметическим способом, так как придётся составлять две пропорции. Помимо обсуждения вопросов и заданий, приведён- ных в №303, учащиеся могут выполнить краткую запись и оформить решение задачи в тетради. На дом: N298, 299, 305. УPOK 11. ЗАДАНИЯ 304, 306-313 Іfель. Продолжить формировать умение составлять про- порции при решении задач. Задачу №311 советуем начать с преобразования отноше- ния, которое шестиклассники могут сделать сами, без помо- щи учителя. Полученный результат можно обсудить и выяс- нить, что показывает отношение 1 : 3 (стоимость переплёта составляет 1 часть от стоимости книг, или переплёт дешевле книг в 3 раза). После обсуждения дети записывают решение в тетради. При организации деятельности класса по решению задач №304, 308-310, 312, 313 советуем пользоваться рекомен- дациями к предыдущим урокам. На дом: №306, 307. УPOK 12. ЗАДАНИЯ 314-321 Іfель. Проверить усвоение определений прямой и обрат- ной пропорциональных зависимостей, сформированность умений составлять пропорции при решении задач. Урок можно начать с самостоятельной работы, предло- жив ученикам задачи №315, 316, 317, 318. На выполнение работы отвести 15-20 минут урока. Остальное время посвятить анализу самостоятельной ра- боты и решению задачи №319. На дом: №314, 320, 321. § 7. Осевая симметрия 2 часа, задания 322-331 |
