матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb. Скачать 2.01 Mb.
|
|
часть). Затем фор- мулируют это же задание, используя понятие ‹отношение›. (Запиши отношение 1 см к 5 см.) На доске появляется запись 5, её можно представить в виде дроби Остальные пункты данного задания учащиеся самостоя- тельно выполняют в тетрадях, а на доске выписывают толь- ко ответы — как верные, так и неверные. Например, записи ответов к пункту 6) могут выглядеть вот так: 15 Вполне возможно, что все дети выполнят задание верно и учтут, что первая величина выражена в сантиметрах, а вто- рая — в дециметрах. В этом случае на доске появятся такие записи: 6 15; 2 5; Рекомендуем учителю дополнить эти верные записи не- верными, чтобы в процессе обсуждения ребята не только отметили, что предложенный вариант ответа неверный, но и указали бы причины допущенных ошибок. На дом: № 174. УPOK 31. ЗАДАНИЯ 178-183 Іfель. Создать дидактические условия для овладения умением упрощать отношения. Рекомендуем начать урок с №178, при выполнении ко- торого учащиеся повторяют ранее изученные вопросы (со- отношение единиц длины и нахождение части от числа) и осмысливают их в контексте нового содержания. По усмот- рению учителя задания можно выполнить или письменно ИЛИ CTHO. С термином «упрощение» школьники познакомились в 5 классе при освоении темы ‹Числовые и буквенные вы- ражения. Уравнения». В 6 классе дети выполняли преобра- зования дробей и дробных выражений. В № 179 термин ‹упростить» впервые упоминается в свя- зи с понятием «отношение». Записав каждое из данных от- ношений в виде дроби, ребята могут сами предложить со- кратить её, то есть разделить и числитель, и знаменатель дроби на одно и то же число 12 18 2 3; №180 (1-й и 2-й столбцы) учащиеся выполняют в те- традях самостоятельно. При фронтальной проверке выясня- ются допущенные ошибки. Они выносятся на доску и об- суждаются. Работу с №181 можно начать с анализа преобразований отношений, написанных на доске, например: а) 0,03 0,4 = г) 1,05 3,5 0,03 0,4 1,05 3,5 = 3 4 (‹ловушка»); 105 35 («ловушка»); ж) 1,8 : 0,2 = 18 : 2 = 9 : 1. После их обсуждения дети самостоятельно выполняют № 181 (6, д, з). Находя отношения величин углов в задании №182, уче- ники повторяют ранее изученные вопросы: определение и свойства углов (развёрнутый и смежный углы), упражняют— ся в упрощении отношений и в измерении углов с помощью транспортира. Например: ШВК:ZKBC—90° : 90° = 1 : 1. В №183 (а, 6) выполняются обратные действия: по данно- М OTHOШeHИЮ ВЕЛИЧИН FЛOB ШКОЛЬНИКИ СТ{ЭОЯТ FЛЫ С ПО- мощью транспортира. Советуем, рассматривая каждое отно— шение, пояснять, что оно показывает. Например, отношение 1 : 2 означает, что один угол составляет половину другого угла, то есть часть другого угла, а отношение 2 : 1 показывает, что один угол больше другого в 2 раза. Это поможет ученикам понять, что на 180° (сумму двух смежных углов) приходится 3 части (180° : 3 = 60°, один угол 60°, другой 120°). Последовательность работы в тетрадях может быть раз- ной: кто—то сначала изобразит развёрнутый угол, а потом построит один из смежных углов; другие начертят сначала один угол, затем другой и получат в результате развёрнутый (полезно рассмотреть оба способа). На дом: № 180 (ж—м), 181 (в, е, и), 183 (в, г). УPOK 32. ЗАДАНИЯ 184-190 Ifenь. Продолжить формирование умений упрощать от- ношения и выражать данные отношения в процентах; совер- шенствовать умение решать задачи. № 184 выполняется устно. Учащиеся анализируют ри- сунок, на котором одна часть прямоугольника закрашена, а 4 части не закрашены; упрощают (если это необходимо) записанные в виде дробей отношения и выбирают из них те, которые отвечают требованию задания 1. 9. 3 5 45’ 15 Ответ на дополнительный вопрос может выглядеть так: Каково отношение площади закрашенной части пря- моугольника к площади всего прямоугольника? Запиши отношение площади закрашенной части пря- моугольника к площади всего прямоугольника. № 185 ученики выполняют самостоятельно в тетрадях. Рассмотрев рисунок, они записывают сначала отношение длины прямоугольника к его ширине (8 : 3), а затем при- ступают к пункту а), рассуждая так: «Найдём длину одно- го из отрезков, на которые разделена длина прямоуголь- ника, 16 : 8 = 2 (см). Вычислим ширину прямоугольника, 3 = 6 (см). Теперь можно вычислить периметр и площадь прямоугольника›. Аналогично шестиклассники будут рас- суждать при выполнении пункта 6), который рекомендуем включить в домашнюю работу. Прежде чем приступить к №186, советуем записать на доске различные варианты размеров прямоугольников, обо- значив буквой а его длину, а буквой b — ширину: 1) а = 6 см, 2) п = 48 см, 3) п = 24 см, 4) а = 27 см, b — 4 см; b — 34 см; b — 16 см; b — 18 см и т. д. Далее учитель предлагает выбрать размеры прямо- угольников, которые соответствуют условию задания, то есть ширина и длина находятся в отношении 2 : 3 (1), (3), (4). Затем ученики самостоятельно чертят в тетрадях прямо- угольник с отношением сторон 2 : 3, не повторяя тех разме- ров, которые были записаны на доске (при построении пря- моугольников ученики ориентируются на количество клеток: 1 см равен 2 клеткам). Построив прямоугольник, вычисляют его площадь и периметр. Полезно обсудить на доске неверные варианты выполнения задания даже в том случае, если никто из детей не допустил ошибок. 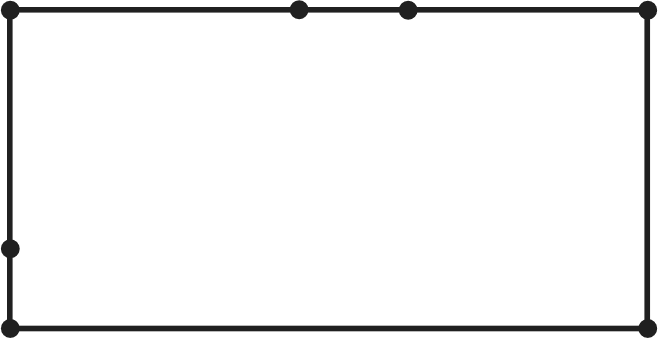 Учитель может сам изобразить на доске, например, такие рисунки: Учитель может сам изобразить на доске, например, такие рисунки:Этот вариант неверный, так как ширина разделена на две неравные части, а длина — на три неравные части. 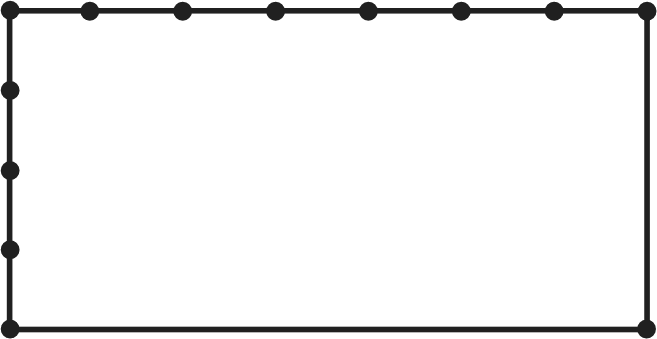 Этот вариант не соответствует условию задания, так как в нём отношение ширины и длины прямоугольника равно 4 : 7. 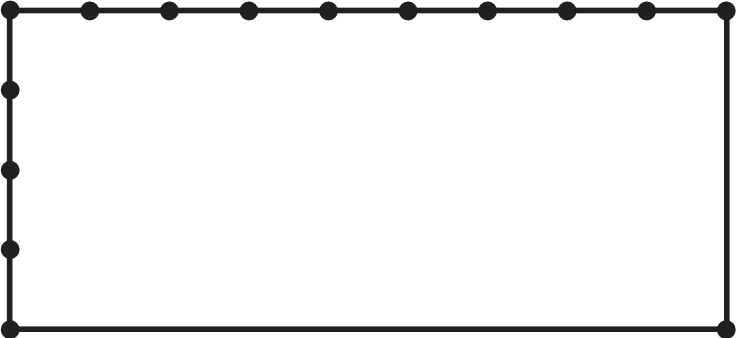 Этот вариант тоже неверный, так как отношение ширины к длине равно 4 : 9. Если его упростить, то получим отноше- ние 2 : 4,5. Выполнение пунктов а) и 6) в №186 можно организо- вать по вариантам: 1-й вариант — а), 2-й вариант — 6). Затем учащиеся обмениваются тетрадями и проверяют друг у друга результаты самостоятельной работы. № 187 (а) сначала обсуждается фронтально и составля- ется план его выполнения: 1) начертить угол в 90 градусов, узнать, сколько градусов приходится на 1 часть, 3) на 7 частей, 4) на 8 частей, 5) разделить угол в данном отношении. №188 (а, 6) ученики выполняют самостоятельно, запи- сывают полученные ответы на доске (как верные, так и не- верные) и затем обсуждают их. № 189 обсуждается фронтально и выполняется устно. № 190 выполняется устно. Дети в парах анализируют ответы Миши и Маши и отвечают на поставленные вопро- сы. Желательно выслушать тех, у кого мнения не совпали. (Ошибся Миша, так как он записал отношение величин, вы- раженных в разных наименованиях.) На дом: № 185 (б), 187 (6, в), 188 (в—д). УPOK 33. ЗАДАНИЯ 191-196 Іfель.Совершенствовать умения упрощать отношения и выражать их в процентах в процессе решения задач, вы- полнять округление чисел. Задание № 191 сначала обсуждается в парах. Ученики вспоминают, как записать полученную дробь в виде процен- тов. После фронтального обсуждения шестиклассники выпол- няют в тетрадях задания а), 6) по вариантам. Одни действуют, как Миша, а другие — как Маша. При проверке задания сле- дует повторить правила округления чисел. № 192. Дети формулируют вопросы задания, используя понятие ‹отношение», и записывают в тетради ответы в пунк- тах 6) и в). Обязательным условием достижения цели урока является понимание того, что для ответа на вопрос ‹Сколько процен- тов ...?» необходимо сначала определить то отношение, ко- торое нужно выразить в процентах. Поэтому после чтения №193 советуем выяснить, как ребята понимают вопрос: Сколько процентов учеников написали работу на «4» и •5»? Учащиеся могут по—разному выразить свою мысль, но важно, чтобы смысл их высказываний сводился к тому, что прежде нужно найти отношение числа учеников, написав- ших работу на «4» и ‹5», к числу всех учеников в классе. Следует не упустить из виду, что в вопросе: ‹Сколько про— центов учеников написало работу на ‹4› и ‹5›?› присутствует союз «и», то есть это 7 и 14 учеников вместе. Только записав отношение 21 : 28, можно ответить на поставленный вопрос. (21 28 Рекомендуем обсудить вопросы: Сколько процентов учеников написало контрольную работу на ‹5›? (7 28 Сколько процентов учеников написало контрольную работу на ‹4›? (14 28 = Обратите внимание класса на то, что 25% + 50a = 75a. Отвечая на вопрос «Сколько процентов учеников написа- ло контрольную работу на ‹3›?», целесообразнее рассмотреть два способа действия. Один требует записи отношения чис- ла учеников, написавших работу на «3», ко всем ученикам класса: 1) 7 + 14 = 21 (уч.); 2) 28 — 21 = 7 (уч.); 3) 7 28 = 7 1 28 4 = 0,25 = 25%. Другой способ связан с пониманием того, что все учени- ки класса приняты за 100% (100% — 75a = 25%). В зависимости от состава класса учитель может сначала либо обсудить фронтально план решения задачи, обратив вни- мание учащихся на указанные выше вопросы, либо сначала предоставить ученикам возможность выполнить задание само- стоятельно, а затем обсудить результаты проделанной работы. После чтения №194 шестиклассники могут самостоя— тельно записать отношение числа учеников, которые зани- маются спортом, к числу всех учеников в школе (600 : 950). Дальнейшие их действия определяются вопросом задачи: «Чему равно отношение ...?» Поэтому можно сразу выпол- нить деление 600 : 950. Получив ответ 0,631, школьники в со— ответствии с требованием задания округляют его до сотых. Советуем, однако, продолжить работу и выразить полу- ченный результат в процентах, а затем упростить отношение 600 : 950. Задачу №195 можно обсудить в парах и записать её решение, а дополнительное задание к ней обсудить затем фронтально. Приступая к работе с заданием №196, учитель предла- гает детям начертить в тетрадях квадрат и наблюдает за их работой. Примите во внимание то, что длину стороны квадрата не следует обсуждать с учениками, тем более не нужно её фиксировать (брать определённое значение). Школьники ра- ботают самостоятельно. Затем учитель говорит: ‹Увеличьте одну сторону квадрата на четверть, а другую — уменьшите на четверть и начертите прямоугольник с полученными сто— ронами›. Если дети затрудняются в восприятии задания на слух, следует обратиться к тексту учебника (с. 44). Педагог может изобразить квадрат на доске или прикре- пить к доске модель квадрата из плотной бумаги, а рядом мо- дель прямоугольника, длины сторон которого соответствуют условию задания. Работая в тетрадях, ученики, скорее всего, разделят сторону квадрата на 4 равные части, и, продолжив сторону квадрата уменьшат на её 41 Ч£tCTЬ. В этом случае ри- сунок в тетради будет выглядеть так: 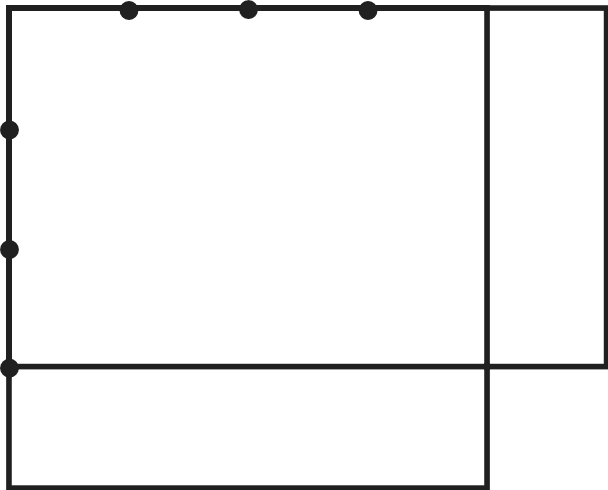 Для проверки можно выяснить, каково отношение дли- ны и ширины полученного прямоугольника, и предоставить шестиклассникам возможность самостоятельно ответить на вопрос: «Чему равно отношение площади данного квадра- та к площади полученного прямоугольника?» Ответ на этот вопрос будет свидетельствовать о том, насколько осознанно ребята усвоили понятие «отношение». Вполне возможно, что одни ученики будут измерять стороны квадрата и прямо- угольника, находить их площадь и только после этого запи- шут требуемое в задаче отношение. Другие выполнят запись: 4 4 6 5 3 15 = 16 15. Следует обсудить, нужно ли измерять длины сторон ква- драта и прямоугольника или можно сразу записать отноше- ние их площадей. (Легко убедиться в том, что ответы при любом способе получаются одинаковыми.) Выполнив деление 16 : 15 и округлив полученный результат до сотых, получаем ответ 1,07, который показывает, что пло— щадь квадрата в 1,07 раза больше площади прямоугольника. На дом: № 191 (в), 192 (а). УPOK 34. ЗАДАНИЯ 197-202 Ifenь.Совершенствовать умение выражать отношения в процентах. После проверки домашнего задания ученики составляют план решения №197. Запись решения задачи можно вклю- чить в домашнюю работу. Выполнение №198 рекомендуем организовать по вари- антам: первый вариант работает с рисунком , второй ва- риант с рисунком Ученики выполняют самостоятельно необходимые измерения и записывают отношение, в кото- ром перпендикуляр BD, проведённый из вершины В, делит сторону АСна две части. Длина каждой части измеряется в миллиметрах. Для рисунка получаем отношение 10 : 35 или 2 : 7. Оно показывает, во сколько раз отрезок ADменьше отрезка DC. Работа с рисунком выполняется аналогично (отрезок AD в 1,5 раза больше отрезка CC). J"fe199, 200 сначала обсуждаются фронтально. Желатель- но, чтобы ученики ответили на поставленные в них вопро- сы, не выполняя вычислений, а затем проверили свои от- веты, записав решения в тетрадях. №200 можно включить в домашнюю работу. №201 выполняется самостоятельно, после чего на доске выписываются ответы как верные, так и неверные, которые обсуждаются и корректируются. №202 советуем предложить для самостоятельной рабо- ты и выписать на доске полученные ответы в виде отношений. Вполне возможно, что ученики допустят ошибки, связанные с переводом одних единиц скорости в другие, или сразу запишут отношение 25 1800 и упростят его. При обсуждении ответов сле- дует записать на доске перевод одних единиц скорости в другие. 25 м/с = 1500 м/мин или 1800 м/мин = 30 м/с. А потом записать отношение скоростей: 25 : 30 = 5 : 6; 1500 : 1800 = 5 : 6 и выразить в процентах. На дом: № 197 (запись решения), 200. УPOK 35. ЗАДАНИЯ 203-211 Іfель.Совершенствовать умение выражать отношения в процентах. Урок советуем начать с №204. После чтения задачи рекомендуем задать вопрос: «Мог- ла бы команда получить 3250 очков?» (Нет, так как возмож— ных очков 3200.) Ответ на этот вопрос позволит выяснить, представляют ли школьники ситуацию, описанную в задаче. Можно задать и такие вопросы: ‹Верно ли утверждение, что команда получила 100% очков? В каком случае можно ска- зать, что команда получила 100% очков?» (Если она получит 3200 очков.) Обсудив приведённые выше вопросы, ребята са- мостоятельно записывают решение задачи. Учителю следует иметь в виду, что возможны два способа её решения. Сначала можно найти количество очков, которое при- ходится на 1% (3200 : 100 = 32 (оч.)), а уже потом ответить на вопрос задачи (3184 : 32 = 99,5%). Или вычислить отношение 3184 : 3200 = 0,995 и выра- зить полученную десятичную дробь в процентах (99,5%). №203 (а) учащиеся выполняют самостоятельно. Для проверки на доске выписываются только ответы, которые обсуждаются и корректируются. При выполнении №205 советуем с помощью транспор- тира построить углы, заданные в условии. 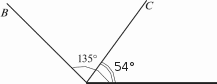 0 А В этом случае учащиеся самостоятельно смогут ответить на поставленные вопросы: = 5 : 2). 135 15 5 Для повторения взаимно обратных отношений советуем обратиться к классу с вопросом: ‹Чему равны отношения ZAOC к ZCOB, ZCOB к ZAOC?•(Эти отношения равны 2 : 3 и 3 : 2 соответственно, то есть будут взаимно обратными.) Задачи №207, 208, 209 шестиклассники решают само- стоятельно. №211 можно предложить учащимся выполнить самостоя- тельно по вариантам. На дом: №203 (6), 206, 210. УРОКИ 36, 37. ЗАДАНИЯ 212-219 Іfель.Совершенствовать умение находить отношение и выражать его в процентах. Познакомить учеников с по- нятием ‹масштаб». Раскрыть взаимосвязь понятий ‹отноше- ние» и ‹масштаб›. Урок можно начать с задачи №212. Рекомендуем исполь- зовать схему, данную в учебнике, и обсудить, как на ней от- ражено отношение возраста сына к возрасту отца, составить план решения задачи, обсудить различные способы её ре- шения. Интересно также выяснить, понимают ли учащиеся, на какой вопрос задачи помогает ответить схема, а на какой вопрос задачи можно ответить, пользуясь данным в условии отношением. Решение задачи одним из способов дети запи- шут в классе, другими способами — дома. Ответы на все вопросы в №213 можно получить, поль- зуясь отношением: 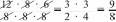 3 3 3 3= 9 : 8. 2 4 Переходя к изучению понятия «масштаб›, следует выяс- нить, встречали ли ученики раньше это слово. Возможно, кто- то из детей попытается объяснить, что оно означает, или опи- шет те ситуации, в которых его возможно использовать. Затем ученики открывают учебник и читают определение масш- таба (с. 47.) Чтобы выяснить, как дети поняли определение масштаба, учитель предлагает им самостоятельно выполнить №215. Учитель рисует на доске схему (No 215): 30 км  АВ и комментирует её: «Расстояние от пункта Адо пункта В на плане обозначено отрезком в 3 см. Каков масштаб пла- на, если на местности соответствующее расстояние равно 30 км?» Прежде чем ответить на мой вопрос, — говорит педа- гог, — давайте ещё раз вслух прочитаем определение масшта- ба: «Отношение длины отрезка на плане к длине соответ- ствующего отрезка на местности называют масштабом». После этого все желающие выходят к доске и записыва- ют ответы на вопрос: ‹Каков масштаб плана?› (Ответы могут быть как верными, так и неверными.) Если вариантов мало или один и тот же (верный) вариант повторяется, учитель за- писывает на доске, например, такие варианты ответов: 3 30; 1 10; з . 1 30’ 10 3 300 000; 1 10 000; 1 100 000; 30 3; i . 3 10000’ 300000 Давайте обсудим выражения на доске, — предлагает педагог. Ученики комментируют каждую запись. Например, 3 : 30 — ответ неверный, так как записано отношение вели- чин, выраженных в различных наименованиях. Дети могут сказать об этом так: ‹Ответ неверный, так как 3 — это сан- тиметры, а 30 — километры». Есть ли на доске запись, в которой величины выраже- ны в одних наименованиях? (Да.) Сколько в 1 км метров? (1000 м) Сколько в 1 м сантиметров? (100 см) Чему равны 3 км, выраженные в сантиметрах? (300 000 см) Верно ли утверждение, что отношение 3 : 300 000 равно отношению 1 : 100 000? (Верно.) Учитель задаёт классу приведённые выше вопросы, если учащиеся затрудняются в выборе масштаба плана. Следует иметь в виду, что причиной этих затруднений может быть как непонимание определения масштаба, так и незнание со- отношений единиц длины. Поэтому советуем записать их на доске (1 км = 1000 м; 1 м = 100 см; 1 км = 100 000 см) и про- должить работу по разъяснению понятия «масштаб›. Педагог рисует на доске схему: 30 км  АВ и обращается к классу: А теперь расстояние в 30 км обозначено на плане от- резком в 1,5 см. Каков масштаб плана? Задание выполняется учениками самостоятельно в тетра- дях. Ответы выписываются на доску. Рекомендуем вызвать тех учеников, которые в предыдущем задании допустили ошибки. После чтения №216 учитель предлагает тем ребятам, которые считают, что деталь будет короче в масштабе 1 : 5, поставить в тетрадях, например, такой значок (*), а тем, кто считает, что деталь будет короче в масштабе 1 : 4, поставить галочку. На доске педагог записывает 1 : 5 (*) и 1 : 4 (J). Че- рез 1-2 минуты станет ясно, кто из шестиклассников не по- нимает, что такое масштаб. Советуем дать возможность обо— сновать ответ тому ученику, кто допустил ошибку (выбрал масштаб 1 : 4). Что обозначает запись 1 : 4? (На плане 1 см обозначает 4 см реальной длины детали.) Какой же длины будет на этом плане изображение де- тали, например, длиной 25 см? (25 : 4 = 6,25 (см).) А какой длины будет изображение детали длиной 25 см на плане, масштаб которого 1 : 5? (25 : 5 = 5 (см).) Следует иметь в виду, что варианты обоснования ответов могут быть и другими. Например, масштаб 1 : 4 показывает, что длина детали на плане составляет |
