матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту

• Название: Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
• Анкор: матем метод 6 кл
• Дата: 08.04.2022
• Размер: 2.01 Mb.
• Имя файла: Matem-Metod-6kl_Text (1).docx
• Тип: Методическое пособие; #455623
• страница: 18 из 25

УPOK 7. КОНТРОЛЬНАЯ РАБОТА №5
УPOK 8. АНАЛИЗ КОНТРОЛЬНОЙ РАБОТЫ №5

§ 14. Сложение и вычитание рациональных чисел

12 часов, задания 516-602

В результате изучения темы учащиеся усвоят правила сложения рациональных чисел с одинаковыми и разными знаками; правило вычитания рациональных чисел; понятие

‹алгебраическая сумма» и форму её записи; правило нахож- дения длин отрезков по координатам их концов; правила раскрытия скобок.

УPOK 9. ЗАДАНИЯ 516-521

Јfель. Сформулировать правило сложения рациональных чи- сел с одинаковыми знаками, используя понятие «модуль числа». Для постановки учебной задачи учитель может ориенти- роваться на задание №516. Записав на доске пары выраже- ний из этого задания, он обсуждает с учениками ответы на поставленные вопросы. Если возникнут трудности, можно обратиться к диалогу Миши и Маши. В любом случае этот диалог следует прочитать, хотя вполне возможно, что учащи- еся дадут примерно те же ответы и самостоятельно сформу-

лируют правило, приведённое в учебнике на с. 116.

В дополнение к координатной прямой в качестве на- глядного пособия можно воспользоваться моделью термоме- тра с подвижным стержнем, употребляя при демонстрации знакомую детям терминологию (‹температура повышается»,

«температура понижается»).

Положительные числа шестиклассники складывать уме- ют. Поэтому следует рассмотреть как можно больше случаев сложения отрицательных чисел.

Использование термометра с подвижным стержнем по— могает школьникам самостоятельно сделать обобщение. Например, учитель демонстрирует (с помощью термометра с подвижным стержнем или его модели) ситуацию: днём температура воздуха была —3°, а к вечеру понизилась на 5°.

На доске выполняется запись: —3 + (—5) = —8. Рассмотрев 5-6 аналогичных ситуаций и выполнив соответствующие записи, ученики пытаются сформулировать правило сложе- ния отрицательных чисел.

На доске можно выполнить №517, в тетрадях №519. После чтения правила на с. 117 ученики самостоятельно вы- полняют в тетрадях №520 (a—e).

На дом: № 518, 520 (ж—м), 521.

УPOK 10. ЗАДАНИЯ 522-526

Lfeль. Сформулировать правило сложения рациональных чисел с разными знаками.

Так же, как и на предыдущем уроке, использование тер- мометра с подвижным стержнем и изображение сложения чисел на координатной прямой помогает учащимся самосто- ятельно сделать обобщение.

Учитель предлагает различные ситуации, демонстрирует их на термометре, а дети записывают в тетрадях соответ- ствующие равенства.

Желательно подбирать пары ситуаций, чтобы числа, по- лученные в результате сложения, были противоположными. Например, а): утром температура была —1°, а днём она повысилась на 8°. Ученики выполняют в тетрадях запись:

—1 + (+8) = 7. В случае 6): днём температура была +1°, а к ве- черу она понизилась на 8°. Ученики демонстрируют ситуацию на модели термометра и выполняют запись 1 + (—8) = —7. Рас- смотрев 4-5 подобных пар ситуаций и выполнив записи вида:

1) 3 + (—7) = —4, 2) 9 + (—3) = +6,

—3 + (+7) = +4; — 9 + (+3) = —6;

дети пытаются сформулировать правило сложения рацио- нальных чисел с разными знаками.

Пользуясь изображением сложения на координатной пря- мой в №522, учащиеся самостоятельно выполняют задание в тетрадях.

В №523 и 524 шестиклассники действуют также с по- мощью координатной прямой.

№525 советуем предложить учащимся для работы в пa- pax, чтобы они выбрали верные утверждения, а после это- го в процессе фронтальной беседы обосновали свой выбор. Обосновывая свой выбор в пунктах а), 6), в), г), ж), школь- ники ссылаются на правила выполнения действий с раци- ональными числами, приводят конкретные примеры, под- тверждающие данные высказывания.

Для доказательства того, что утверждения д) и е) не- верные, используются контрпримеры: 3 + (—7) = —4 или

—5 + (—6) = —11 0.
N 526 для самостоятельного поиска информации ‘

из истории математики.

На дом: №523 (д—з), 524 (ж—м).

УPOK 11. ЗАДАНИЯ 527-535

Іfель. Создать дидактические условия для приобретения опыта в сложении рациональных чисел.

№527 обсуждается фронтально. Поясняя ответы в пун- ктах a)—г), ученики пользуются правилами сравнения рациональных чисел, а в пунктах д)—з) — правилами сложе- ния рациональных чисел с одинаковыми и разными знака- мИ.

Используя таблицу в №529, ученики самостоятельно со- ставляют равенства и записывают их в тетрадь.

№530 (a—r) для устной работы. При его выполнении учащиеся пользуются прикидкой, т. к. достаточно опреде- лить только знак суммы.

№531 учащиеся выполняют устно. Определяя знак каж- дой суммы, они отмечают, какие числа (с одинаковыми или разными знаками) складываются, сравнивают их модули и делают вывод относительно знака суммы. Например:

а) 0,785 + (—1,384); складываем числа с разными знаками; модуль отрицательного числа больше, следовательно, значе- ние суммы — число отрицательное;

д) (—0,7) + (—0,215); складываем числа с одинаковыми знаками; нужно сложить их модули и поставить знак «—».

Затем шестиклассники самостоятельно записывают ра- венства в тетради и выполняют вычисления (1 столбец).

№532 также сначала обсуждается фронтально. Сравни- вая выражения в каждой паре, дети отмечают, что слагаемые в каждой паре отличаются знаками, но модули их одинако- вы. Значит, слагаемые в первой строке являются числами, противоположными слагаемым во второй строке. Поэтому, вычислив значения первого и второго выражений в каждой паре, получаем числа противоположные. Ученики выполня- ют самостоятельно вычисления, обмениваются тетрадями и проверяют друг у друга результаты.

В №533 требуется установить, чем похожи все выра- жения (это сумма двух отрицательных чисел). Фронтально обсуждается, какое слагаемое нужно заменить противопо- ложным числом, чтобы значение суммы было положитель- ным. Для обоснования ответа ученики пользуются прави- лом сложения чисел с разными знаками. Например, в сумме

—4 + (—0,57) нужно первое слагаемое заменить числом 4,

а в сумме — (—0,375) первое слагаемое заменить десятичной

дробью 0,5. Далее, складывая числа с разными знаками, мы из модуля большего числа вычтем модуль меньшего чис- ла и поставим знак числа, модуль которого больше, то есть получим число положительное. Это можно сделать по вари- антам {1-й вариант— в), г); 2-йвариант— д), е)), Учени- ки самостоятельно записывают в тетрадь новые выражения и вычисляют их значения.

Из №534 в классе выполняются а) и в), из №535 — а) и г). На дом: №528, 530 (д—з), 534 (r—e), 535 (6, в, д, е).

УPOK 12. ЗАДАНИЯ 536-542

Іfель. Создать дидактические условия для приобретения опыта в сложении рациональных чисел.

Для сравнения чисел в №537 шестиклассники использу- ют: а), 6) основное свойство дроби; в) утверждение о том, что любое отрицательное число меньше любого положительного; г) сокращение дробей и приведение их к общему знаменателю. После сравнения данных в задании чисел полезно про-

должить с ними работу, например, найти их сумму.

При выполнении №538 следует иметь в виду, что возмож- ны различные варианты ответа — в пунктах а) и 6). Например, отрицательной будет сумма чисел —30 и 5; 5 и —17; —30 и —17; —28

и 5 и т. д.Положительной будет сумма чисел 32 и —17; 32 и —5; 5 и 32. Сумма равна нулю при сложении противоположных чисел 5 и —5. После самостоятельной работы с этим заданием школьники выписывают на доску равенства и обсуждают их. Аналогично организуется деятельность учащихся при выполнении №539. Учащиеся самостоятельно записывают в тетрадях равенства, которые соответствуют каждому из пунктов: а) 5 + 3 = 8; 6) —7 + (—2) = —9; в) —8 + 0 = —8;

г) 9 + (—9) = 0.

№540, 541, 542 рекомендуем обсудить и выполнить в классе.

На дом: №535 (ж—и), 536.
УPOK 13. ЗАДАНИЯ 543-552

Іfель. Сформулировать правило вычитания рациональ- ных чисел. Сформировать умение заменять вычитание раци- ональных чисел сложением.

Для подготовки учащихся к восприятию и пониманию правила вычитания рациональных чисел советуем выписать

пары выражений из №543 и предложить школьникам отве- тить на вопросы.

Как показывает практика, все ученики замечают, что в первом выражении выполняется сложение, а во втором — вычитание.

Помимо этого, некоторые дети замечают, что во втором выражении каждой пары вычитают число, противоположное второму слагаемому. Таким образом, ответ на первый вопрос

№543 не вызывает у школьников затруднений.

Проблема в том, как ответить на второй вопрос этого задания: ‹Верно ли утверждение, что значения выражений в каждой паре одинаковы?» Возникает проблемная ситуация, для разрешения которой учитель предлагает найти значения первых выражений в каждой паре. С этим ученики могут справиться самостоятельно, т. к. они научились складывать отрицательные числа и числа с разными знаками. В тетра- дях появляются записи:

3
а) ₄ + (—5) —5

₆₎ 7 + + 5 2 .

8 8 8

в) —4 + +6 ⁱ

2

= 2 ₂

• 
  Предположим, что во втором выражении получились такие же результаты. Какие равенства вы запишете? — обра- щается учитель к детям.
  

В тетрадях появляются записи:

з
а) ₄

— (+5) —5 ³ 6)

4

в) —4 — —6 ⁱ 2

2

— Как можно проверить, верно ли наше предположение? Педагог может напомнить, что ‹пока мы умеем только скла- дывать рациональные числа». Если никаких мнений не по- ступит, то учитель предлагает прибавить к разности вычитае- мое и спрашивает: «В каком случае мы можем утверждать, что записанные равенства верные?› (Если в результате сложения разности и вычитаемого получится уменьшаемое, значит, ра-

венства верные.) В тетради появляются записи:

а) —5 ³

4

+ (+5) = ³ 6)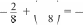

4

в) 2 ⁱ

2

+ —6 ¹ —4.

2

Дети подводят итог:

— Мы получили уменьшаемое, значит, предположение было верным, значения выражений в каждой паре одинаковы.

— Какой вывод мы можем сделать в результате проделан- ной работы? — спрашивает учитель.

Если ученики затрудняются, они открывают учебник на с. 124, где записано правило. (Чтобы из одного рациональ- ного числа вычесть другое, надо к уменьшаемому прибавить число, противоположное вычитаемому.)

№544 позволяет проверить, как учащиеся поняли новое для них правило замены вычитания сложением. Школьники выбирают пары выражений, в которых вычитание заменяет- ся сложением. Учитель акцентирует их внимание: 1) на заме- не знака действия; 2) на том, что в соответствии с правилом нужно прибавить противоположное число. Например, в паре выражений пункта г) знак действия вычитания поменяли на сложение, но прибавили то же число, не поменяв знак на противоположный. Значит, пара выражений в пункте г) не соответствует требованию задания.

При обсуждении №545 выясняется, что ставить знак «+» перед положительным числом необязательно: если число на- писано без знака, то оно положительное. Например, выраже- ние л) 16 — 20,7 можно переписать так: 16 — (+20,7); выраже-

ние 6) 8,3 — 6,1 можно записать так: 8,3 — (+6,1) и т. д.Советуем выполнить эти записи на доске, т. к. они помогут шестикласс- никам лучше понять правило замены вычитания сложени- ем при выполнении действий с рациональными числами. В выражении в) —7,2 — 4,1 перед числом 4,1 стоит знак действия вычитания, то есть из отрицательного числа вычи- тается положительное. Заменив вычитание сложением, запи-

шем —7,2 + (—4,1).

В указанном выше задании ученики упражняются в за- мене вычитания сложением и затем вычисляют результат. Записи в тетрадях имеют вид:

а) 83,2 — (—3,2) = 83,3 + 3,2 = 86,4;

л) 16 — 20,7 = 16 + (—20,7) = —4,7;

в) —7,2 — 4,1 = —7,2 + (—4,1) = —11,3.

Каждую запись учащиеся комментируют:

— Заменяем вычитание сложением, меняем знак вычита- емого на противоположный и вычисляем результат.

При выполнении №546 советуем использовать де- монстрационный термометр с подвижным стержнем. Как

показывает практика, наблюдая движение стержня, дети дают правильный ответ (Температура повысилась на 12°.).

После этого можно интерпретировать данную ситуа- цию на графической модели. Учащиеся чертят в тетрадях координатную прямую и изображают на ней изменение тем- пературы.

+12

—10 0 2
Затем обсуждается выражение 2 — (—10), обозначающее разность температур (той, которая стала, и той, которая бьша). Заменив в этом выражении вычитание на сложение 2 + 10, школьники получают ответ (12), соотносят его с изображени- ем на координатной прямой и делают вывод: температура по- высилась на 12°.

№547 можно обсудить фронтально или предложить ре- бятам выполнить задание самостоятельно. В первом случае, выбирая координатную прямую (2), соответствующую зада- нию, ученики обычно ориентируются на направление стрел- ки дуги (была +5°, стала —3°). Значит, изменение температу- ры в виде разности нужно записать так: —3 — (+5).

Заменив сложение вычитанием, получаем:

—3 + (—5) = —8, то есть температура понизилась на 8°.

Использование предметной (термометр) и графической (координатная прямая) моделей создаёт благоприятные ди- дактические условия для понимания и усвоения операций, которые выполняются при вычитании рациональных чисел (замена действия вычитания на сложение с числом, противо- положным вычитаемому) и подготавливает учащихся к вос— приятию понятия ‹алгебраическая сумма».

Во втором случае, выполняя №547 самостоятельно, дети сначала выберут координатную прямую, на которой изобра- жено изменение температуры. После обсуждения выбранной координатной прямой шестиклассники записывают в тетра- дях изменение температуры в виде разности. Ответы уча- щихся, как верные, так и неверные, следует вынести на доску и проанализировать. Затем ребята самостоятельно найдут значение разности, заменив вычитание сложением. Работу с заданием можно продолжить, предложив учащимся опи- сать ситуацию, изображённую на рис. 1 в учебнике. (Ночью температура воздуха была —3°, а днем стала +5°. На сколько

градусов изменилась температура?) Изменение температуры записывается в виде разности 5 — (—3) и вычисляется значе- ние этого выражения (5 + 3 = 8).

Ответ: температура повысилась на 8°.

Для ответа на вопрос №548 достаточно привести кон- кретный пример. Пусть даны числа —2 и —7. Запишем раз- ность этих чисел —2 — (—7). Вычислим значение разности, заменив вычитание сложением: —2 — (—7) = —2 + 7 = 5. За-

пишем сумму данных чисел: —2 + (—7) = —9; 5 —9. Значит, разность двух рациональных чисел может быть больше, чем их сумма.

Для обоснования ответов в №549, 550 учащиеся запи- сывают в тетрадях по 2-3 равенства, которые соответствуют требованию каждого задания. Советуем эти равенства выне- сти на доску и обсудить.

№549. Разность двух рациональных чисел может быть больше уменьшаемого: —2 — (—9) = —2 + 9 = 7; 7 —2.

№550. Разность двух рациональных чисел может рав- няться уменьшаемому (—7-0 = —7; 8-0 = 8).

№551 обсуждается сначала устно. Дети находят правило, по которому составлен каждый ряд:

а) каждое следующее число увеличивается на 3;

в) каждое следующее число увеличивается на 2;

6) ряд составлен по правилу: увеличить на 3, уменьшить на 2 и т. д.;

г) ряд составлен по правилу: уменьшить на 4, увели- чить на 3. Затем ребята записывают в тетрадях данные ряды и продолжают каждый ряд ещё на 3 числа.

№552. Сначала шестиклассники самостоятельно выпол- няют в тетрадях пункты а), 6), в); затем проверяют работы друг друга и фронтально обсуждают выявленные ошибки.

На дом: 552 (r—e), №545 (г, д, и, к, о, п).