матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту

• Название: Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
• Анкор: матем метод 6 кл
• Дата: 08.04.2022
• Размер: 2.01 Mb.
• Имя файла: Matem-Metod-6kl_Text (1).docx
• Тип: Методическое пособие; #455623
• страница: 19 из 25

УPOK 14. ЗАДАНИЯ 553-560

Lfeль.Познакомить учащихся с понятием ‹алгебраиче- ская сумма›.

После проверки домашнего задания коллективно обсуж- дается №554. Учитель выясняет:

— Чем похожи все уравнения? (В правой части каждого уравнения 0, то есть сумма или разность двух чисел равны 0.)

— Можно ли найти корни уравнений, не записывая их решения?

Предложения учащихся обсуждаются фронтально. Дети могут пользоваться способом подбора, подставляя число, ко- торое в сумме с известным слагаемым дает 0. Выбор корня уравнения следует обосновать на координатной прямой. На- пример:

а) —3,6 + а = 0; —3,6 + 3,6 = 0; а = 3,6 (увеличиваем —3,6

на 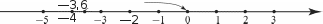3,6).

+36

в) 7,8 — у = 0; 7,8 — 7,8 = 0; у = 7,8 (уменьшаем 7,8 на 7,8).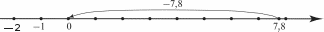





С точки зрения упражнений в сложении и вычитании ра- циональных чисел (особенно отрицательных) и повторения правил взаимосвязи компонентов и результатов действий сложения и вычитания, полезно выполнить запись решения некоторых уравнений.

Например:

а) —3,6 + а = 0; е) х + (—4,5) = 0; в) 7,8 — у = 0;

а—0 — (—3,6); х = 0 — (—4,5); у—7,8 — 0;

а—3,6; х = 4,5; у = 7,8.

№555 учащиеся выполняют самостоятельно (1-й стол- бец) и проверяют результаты друг друга, обмениваясь тетра- дями в парах.

Затем учитель предлагает записать в тетради сумму чисел в №553 (а). Одновременно выполняется запись на доске:

—3,6 + 2,4 + (—8,4) + 0 + (+3,6) + (—1,2).

Чтобы познакомиться с определением нового понятия, дети открывают учебник и читают текст на с. 125, а затем за- писывают выражение на доске в виде алгебраической суммы:

—3,6 + 2,4 — 8,4 + 0 + 3,6 — 1,2.

После записи алгебраической суммы следует ещё раз уточнить, какие числа являются слагаемыми (—3,6; 2,4; —8,4;

0; 3,6; —1,2).

— Какие из них являются положительными числами?
150

• 
  Какие из них являются отрицательными?
  

Важно, чтобы дети поняли, что знак, стоящий перед чис- лом, относится к этому числу.

• 
  На предыдущих уроках мы узнали, что для рацио- нальных чисел выполняется переместительное и сочетатель- ное свойства сложения. Как, используя эти свойства, можно найти значение данной суммы? — спрашивает учитель.
  

Предложения учащихся обсуждаются. Например, —3,6 и 3,6 — противоположные числа, их сумма равна нулю. Те- перь можно сложить отрицательные числа (—8,4 — 1,2 = —9,6) и к полученному результату прибавить 2,4. Получаем:

—9,6 + 2,4 = —7,2.

№553 (6) ученики записывают в виде алгебраической суммы и вычисляют результат.

Затем приступают к фронтальному обсуждению №556. Ответ Миши отличается от ответа Маши тем, что Миша за- писал положительные числа без знака ‹+›.

№557 и №558 (а—в) шестиклассники выполняют само- стоятельно с последующей проверкой.

В этот же урок или в домашнюю работу включаются

№559, 560.

На дом: №553 (в, г), 555 (2 столбец), 558 (r—e).
УPOK 15. ЗАДАНИЯ 561-567

Ifenь. Научить шестиклассников записывать алгебраиче- скую сумму и вычислять её значение.

После проверки домашнего задания ученики выполняют самостоятельно в тетрадях №561 по вариантам.

1-йвариант:а)—в), 2-йвариант:г)—e).

Перед самостоятельной работой педагог советует уча- щимся прочитать правило на с. 125 (вслух) и назвать пункты задания, в которых сумма чисел равна отрицательному чис- лу (a)—r)); положительному числу (д), е)). Результаты само- стоятельной работы проверяются фронтально.

Начать обсуждение №562 можно с вопроса:

• 
  Верно ли утверждение, что значение всех сумм будет положительным числом?
  

Ученики анализируют каждое выражение, обращаясь к пра- вилу сложения чисел с разными знаками, и делают вывод.

После этого вслух читается задание. Учитель выясня- ет, какие из слагаемых нужно заменить противоположным

числом (положительные). Школьники записывают равенства в тетрадях. Проверка осуществляется фронтально.

В №563 проверяется, как школьники усвоили правила сложения рациональных чисел и понятие ‹алгебраическая сумма›. Полезно задать шестиклассникам такие вопросы:

• 
  Какие числа складывают в первой строке пункта а)? (128,3 и —75,6)
  
• 
  Почему сумма в первой строке равна положительному числу 52,7?
  
• 
  Какие числа складывают в третьей строке? (—75,6 и 128,3)
  
• 
  В каких строках пункта а) использовано перемести- тельное свойство сложения?
  

Аналогично организуется деятельность учащихся при выполнении пункта 6). Важно, чтобы ученики поняли, что знак перед числом относится к этому числу, и с данными числами выполняется сложение.

№564 (1-й столбец) можно использовать для самостоя- тельной работы.

При выполнении №564 ученики повторяют разряды в десятичной системе счисления и правила сравнения раци- ональных чисел.

Например, а) 4,15 ... 4,0152 (оба числа положительные, це- лые части равны; сравниваем десятые: слева 1 десятая, спра- ва 0 десятых; ставим знак сравнения);

6) —4,015 ... —4,0152: оба — числа отрицательные; чем боль- ше модуль отрицательного числа, тем меньше отрицательное число; уравняем количество знаков после запятой в каждой дроби и запишем нуль в разряде десятитысячных (получим

—4,0150); модуль числа —4,0150 меньше модуля числа —4,0152,

значит, —4,015 —4,0152.

№565 (1-й столбец) — самостоятельно в тетрадях. Пред- варительно следует обсудить на доске выражение из пункта 6) 1,6 — (—2) — (—8) — (+5) и уточнить, что запись —(—2) озна- чает, что нужно записать число, противоположное числу —2, то есть —(—2) = 2.

Запись выражения 1,6 — (—2) — (—8) — (+5) в виде алгебра-

ической суммы будет выглядеть так: 1,6 + 2 + 8 — 5.

В №566 (а,в) советуем воспользоваться переместитель- ным свойством сложения и сначала упростить данное выра- жение:

4,8 — х + 1,2 +у—2,1 = 3,9 — х + у.

Затем нужно подставить вместо х и у их значения: а) 3,9 — 1,9 — 3 = —1; в) 3,9 — (—1,9) — 3 = 2,8.

№567 обсуждается фронтально. Назвав корень уравне- ния, учащиеся осуществляют устную проверку:

а) х = 385; 385 — 385 = 0; г) у = —17,2; —17,2 + 17,2 = 0;

в) а = —8,3; —8,3 + 8,3 = 0; 6) х = —15,4; —15,4 + 15,4 = 0;

д) а = 14,5; —14,5 + 14,5 = 0; з) b—9,7; 9,7 — 9,7 = 0;

ж) х = 16,9; 16,9 — 16,9 = 0; е) х = —6;—10 — (—6) = —10 + 6 = —4;

и) г = —20; —20 + 18 = —2.

Если шестиклассники испытывают затруднения, напри- мер, при выполнении пункта г), то данное уравнение луч- ше записать в таком виде у + 17,2 = 0 (это можно сделать на доске).

На дом: №564 (2 столбец), 566 (6, г).
УPOK 16. ЗАДАНИЯ 568-573

Lfeль.Сформировать умение находить длину отрезка на координатной прямой.

После проверки домашней работы можно приступить к изучению нового материала.

Учитель изображает на доске координатную прямую, от- мечает на ней две точки, например:

а) А(—3); В(6); 6) С(—8); D(1); в) А (—9); М(—2);

и спрашивает, чему равно расстояние между данными точ- ками. Ученики легко справляются с этим заданием, подсчи- тав число единичных отрезков между точками.

• 
  Предположим, что даны точки с координатами Л(—174) и B(120). Как найти расстояние между ними? — интересуется учитель.
  

Как показывает практика, большинство детей справля- ется с этой конкретной задачей и обычно рассуждают так: точка Л(—174) находится от начала отсчёта на расстоянии 174 единичных отрезка, а точка B(120) находится от начала от- счёта на расстоянии 120 единичных отрезков. Чтобы найти расстояние между точками Аи В,надо сложить расстояние от точки А до начала отсчёта и расстояние от точки В до на- чала отсчёта.

• 
  Для данной конкретной задачи, — говорит учитель, — можно согласиться с предложенным способом, так как он приводит к правильному результату. А если нужно найти расстояние между точками Л(500) и B(300)?
  

Можно воспользоваться схемой:




Складывая расстояния от каждой из двух точек до нача- ла отсчёта, дети обнаруживают, что получается неверный от- вет, и предлагают из большей координаты вычесть меньшую (500 — 300 = 200).

Полезно выяснить, можно ли воспользоваться этим спо- собом при нахождении расстояния между точками А(—174) и В (120):

120 — (—174) = 120 + 174 = 294.

Целесообразно рассмотреть пример, когда координатами обеих точек являются отрицательные числа, и после этого познакомиться со способами, предложенными Мишей и Ма— шей в №568, и обсудить их. Затем дети читают правило на с. 128 и выполняют упражнения (a—r), пользуясь правилом и рассуждая, как Маша.

Для самостоятельной работы на уроке рекомендуем

№569 (1 столбец), №570 (1 столбец), №572 (1 столбец),

№573 (1 столбец).

При проверке результатов самостоятельной работы реко- мендуем комментировать полученные результаты, ссылаясь на правила и определения.

На дом: №568 (д, е), 569 (2 столбец).