матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb.
|
|
§ 17. Решение уравнений 9 часов, задания 713-746 В результате изучения темы учащиеся овладеют спосо— бами преобразования уравнений, которые связаны со свой- ствами равносильности уравнений (термин «равносильность» не вводится); приобретут опыт решения уравнений, в кото- рых неизвестное находится и в левой, и в правой частях (ал- гебраический способ решения уравнений); усовершенствуют умение решать задачи способом составления уравнений. УPOK 43. ЗАДАНИЯ 713-717 Lfeль. Обсудить и сформулировать способ преобразова- ния уравнений: ‹если обе части уравнения умножить или разделить на одно и то же число, не равное нулю, то полу- чится уравнение, имеющее те же корни, что и первое»; фор- мировать умения выполнять преобразования уравнений и решать их, используя данный способ. В начальных классах дети решают простые и усложнён- ные уравнения, в которых неизвестное находится в левой или правой части или является частью одного из компонентов арифметического действия. Помимо этого младшие школьни- ки получают возможность научиться решать арифметические задачи способом составления уравнений. В пятом классе учащиеся совершенствуют умения решать уравнения на основе взаимосвязи компонентов и результатов арифметических действий (арифметический способ). В шестом классе расширение понятия числа предоставляет возможность ввести свойства равносильности уравнений, по- зволяющих решать их алгебраическим способом. К этому вре- мени большинство учащихся уже усвоят содержание понятий ‹уравнение», «корень уравнения», «что значит решить урав- нение›. Свойства уравнений вводятся на основе анализа пар уравнений, в которых одно получается из другого в результате тех или иных преобразований. В начальных классах дети решают простые и усложнён- ные уравнения, в которых неизвестное находится в левой или правой части или является частью одного из компонентов арифметического действия. Помимо этого младшие школьни- ки получают возможность научиться решать арифметические задачи способом составления уравнений. В 5 классе тема: «Буквенные выражения и уравнения» рассматривается во второй раз. Учащиеся совершенствуют умения решать уравнения на основе взаимосвязи компонентов и результатов арифметиче- ских действий (арифметический способ). В третий раз с решением уравнений школьники встре- чаются в шестом классе, где расширение понятия числа предоставляет возможность ввести свойства равносильности уравнений, позволяющих решать их алгебраическим спо- собом. К этому времени большинство учащихся уже усвоят содержание понятий ‹уравнение›, «корень уравнения», ‹что значит решить уравнение›. Свойства уравнений вводятся на основе анализа пар уравнений, в которых одно получается из другого в результате тех или иных преобразований. Пары уравнений из №713 советуем вынести на доску. Учитель предлагает сравнить уравнения в каждой паре и вы- яснить, каким преобразованиям подверглось первое уравне- ние. Шестиклассники анализируют уравнения и читают ди- алог Миши и Маши и свойство уравнений на с. 158. Далее учащиеся выполняют задания, где используется равносильность, но сам термин не употребляется. Выполнение №714 позволяет выяснить, как ученики усвоили новый способ преобразования уравнений. (Верные ответы 6), в)). №715. Дети комментируют решения уравнений, предло— женные Мишей и Машей, и отвечают на вопросы: Как рассуждала Маша? Как рассуждал Миша? (Миша пользовался правилом нахождения неизвестного слагаемого, Маша умножала левую и правую части уравне- ния на число 3.) Затем уравнение а) 1-й вармант решает, рассуждая как Маша, а 2-йвариант—как Миша. Аналогично организуется работа с уравнением в пун- кте 6): 1-йвармантпри решении рассуждает как Миша, а Л-й вариант — как Маша, то есть способы решения урав- нений чередуются. №716 — устно. Решение уравнений а) и 6) дети выполня- ют дома, ориентируясь на уже выполненные преобразования. При выполнении №717 учащиеся могут действовать по— разному, но в результате важно, чтобы они воспользовались рас- смотренным на уроке свойством равносильности уравнений, которое дано в учебнике на с. 160. Например, используя данное свойство равносильности уравнений, ученики могут решить каждое уравнение, сравнить их корни и потом выбрать те урав— нения, корни которых одинаковы. Но целесообразнее поступить по-другому: сначала сравнить между собой уравнения каждого столбца и выявить их сходство и различие, а также обратить внимание на то, что первое дробное выражение в пункте а) от- личается от первых дробных выражений в других уравнениях первого столбца. Поэтому имеет смысл преобразовать первое уравнение, умножив его левую и правую часть на 14. После вы- полненного преобразования уравнение пункта а) принимает вид уравнения, данного в пункте г). То есть уравнения первого столбца в пунктах а) и ж) будут иметь одинаковые корни. С уравнениями второго столбца рекомендуем действовать аналогично. Во втором столбце одинаковые корни имеют урав— нения 6) и г). На дом: №716. УPOK 44. ЗАДАНИЯ 718-723 Іfель.Познакомить учащихся со свойством уравнений: ‹если к обеим частям уравнения прибавить одно и то же чис— ло или буквенное выражение, то получим уравнение, имею- щее те же корни». Сформировать умение выполнять преобра- зования уравнений и решать их, используя данное свойство. Учитель записывает пары уравнений из №718 на доске и формулирует первый вопрос. Как показывает практика, ответ на него не вызывает затруднений у учащихся. (В пункте а) к обеим частям уравнения прибавили —2. Возможен и такой ответ: ‹Из обеих частей уравнения вычли 2». В этом случае следует напомнить учащимся об «алгебраической сумме».) Чтобы ответить на второй вопрос, ученики самостоятель- но записывают в тетрадях решение первого и второго урав- нений из пункта а), открывают учебники и сравнивают свои записи с записями, выполненными Машей. Первая пара уравнений обычно не вызывает вопросов, и дети самостоя- тельно справляются с их решением. Решение второй пары уравнений в пункте 6) создаёт про- блемную ситуацию, разрешение которой требует новых знаний. Учитель знакомит шестиклассников ещё с одним свойст-вом уравнений и предлагает им подумать, какое число или выра- жение следует прибавить к обеим частям второго уравнения в паре 6), чтобы неизвестное оказалось только в одной части. Для проверки понимания прочитанного текста выполня- ется №719. Советуем дать учащимся возможность самосто- ятельно решить уравнение а) и только после этого вынести его на доску и обсудить возможный способ действия. Если ученики поняли свойство уравнений на с. 160, то на доске появятся записи: Зх + х — 2 — х = 4 + х — х (то есть к обеим частям уравнения прибавили выражение (—х), чтобы в результате преобразований уравнения неизвестное оста— лось только в левой его части). Учитель напоминает учащимся, что сумма противопо- ложных слагаемых равна нулю. Зх + х — 2 — х = 4 + х — х; Зх — 2 = 4; Зх = 4 + 2; Зх = 6, х = 6 : 3; х = 2. Пользуясь правилом на с. 160, ученики запишут решение уравнения так: Зх +х—2 = 4 +х, Зх + х — х = 4 + 2 (то есть перенесут с противоположным знаком в левую часть уравнения слагаемое х, а в правую — слагаемое —2); Зх = 6, х = 2. Каждый из способов обсуждается и делается вывод, что целесообразнее пользоваться вторым правилом. Рекомендуем при решении последующих уравнений №719 всякий раз проговаривать правило и делать проверку реше- ния уравнений, т. е. подставлять в исходное уравнение полу- ченное значение переменной и убеждаться в том, что полу- чается верное числовое равенство. На этом же уроке советуем выполнить первую часть из №720 (Объясни ...), а решение уравнений можно включить в домашнюю работу. №721. Пользуясь основным свойством пропорции, учащи- еся записывают каждое уравнение в виде равенства соответ- ствующих произведений. Далее открывая скобки и применяя свойства уравнений, находят их корни и выполняют провер- ку. Полученные результаты целесообразно обсудить фрон- тально. Рекомендуем выполнить в классе №722 (а, 6) и №723 (а, 6), а закончить выполнение этих заданий дома. На дом: №722 (в—е), 723 (в—е). УPOK 45-48. ЗАДАНИЯ 724-737 Іfель. Сформировать умение решать уравнения алгебраи- ческим способом. Совершенствовать умение решать задачи способом составления уравнений. После проверки домашнего задания шестиклассники чи- тают №724. Можно по-разному организовать деятельность учащихся при решении данной задачи. Опишем один из воз- можных вариантов. Учитель предлагает шестиклассникам прочитать текст задачи и выбрать неизвестное, которое можно обозначить буквой х или, как говорят математики, принять за х. Как показывает практика, большинство учащихся ориентируют- ся в ситуации и предлагают обозначить буквой х количество страниц в одной тетради. — Но в задаче речь идёт о двух тетрадях, поэтому нуж- но определиться, какая это тетрадь — та, в которой страниц больше, или та, в которой страниц меньше? Ученики рассуждают: «Если х — количество страниц во второй тетради, то х + 12 это количество страниц в первой тетради. А если х — количество страниц в первой тетради, то во второй тетради х — 12 страниц». Уже на этом этапе некоторые ученики готовы выполнить предложенное в учебнике задание — выбрать уравнения, которые соответствуют задаче. Учитель предлагает шести- классниками записать в тетрадях пункты 1), 3), 2), 4) и по- ставить палочки у тех пунктов, где записаны уравнения, соответствующие задаче. Верными ответами будут 1) и 3). В процессе фронтальной работы ученики обосновывают свой выбор, а также объясняют, почему другие уравнения не соответствуют задаче. Составленные учениками уравнения можно решить либо в классе, либо дома. Представляет интерес и решение задачи арифметическим способом с помощью схемы, которые могут нарисовать либо ученики, либо учитель: 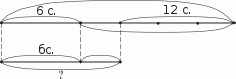 После того, как учащиеся соотнесут текст задачи со схе- мой, они легко запишут её решение по действиям: 12 : 3 = 4 (с.) — осталось во второй тетради; 4 4 = 16 (с.) — осталось в первой тетради; 16 + 6 = 22 (с.) — было в первой тетради; 4 + 6 = 10 (с.) — было во второй тетради. №725. Соотнесение текста задачи с выражениями, дан- ными в пункте а), позволяет ученикам определить, что буквой х обозначена длина всего рейса, и самостоятельно составить уравнение: 0,625x + 24 + 0,25x = х. Решив это урав- нение, дети отвечают на вопрос задачи: 192 км составляет рейс парохода. Пункт в) можно использовать для индивидуальной ра- боты. Если буквой х обозначено расстояние, пройденное за вторые сутки, то можно составить уравнение, предвари-  тельно записав дробь 0,625 в виде обыкновенной (0,625 = ). Уравнение имеет вид: Зх — 5 4x = 24.Решив его, получим х = 48, то есть 48 км пароход про- шёл за вторые сутки. Чтобы ответить на вопрос задачи, надо 48 4 = 192 (км) — рейс парохода. №727. Учащиеся анализируют текст задачи и коммен- тируют ответы Миши и Маши. (Какую величину обозначил каждый из них буквой х, и как они рассуждали при состав- лении уравнений?) Уравнения, составленные Мишей и Ма- шей, дети самостоятельно решают в тетрадях. Затем обсуждается №726. Опираясь на опыт, приоб- ретённый при анализе №727, ученики легко справляются с ответом на вопрос: «Сколько лет назад Лера была в 2 раза старше Саши?›, составив и решив уравнение: 24— х 15 — х = 2; 24 — х = 2 (15 — х); 24 — х = 30 — 2x; —х + 2x = 30 — 24; х = 6. Некоторые ученики, отвечая на вопрос задачи, не состав- ляют уравнение, а подбирают два числа, разность которых равна 9 и одно число в 2 раза больше другого (18 и 9), затем выполняют действия 24 — 18 = 6; 15 — 9 = 6. Назвать другую пару чисел, в которой соблюдаются оба эти условия, оказы- вается невозможным. Шестиклассники убеждаются в этом, составив и решив уравнение: 18+х 9 +х = 2; 18 + х = 2 (9 + х); 18 + х = 18 + 2x; х — 2x = 18 — 18; —х = 0; х = 0. №730. Рекомендуем дать время учащимся для решения задачи с помощью уравнения. Однако, как показывает прак- тика, это достаточно непростое задание для школьников. Поэтому следует фронтально обсудить ответ на вопрос а), для которого шестиклассникам нужно вспомнить, что такое крат- ное сравнение и как найти часть от числа. Если первое число меньше второго в 2,75 раза, значит, второе в 2,75 раза больше первого. Тогда буквой х обозначено первое число, а второе чис- ло — 2,75x. По условию задачи третье число составляет треть от суммы первого и второго чисел, то есть третье число пред- ставлено в виде выражения 1 (х + 2,75x). Это обсуждение по- 3  может детям составить уравнение, для которого желательнозаписать десятичную дробь в виде обыкновенной: 2,75 = 2 . Тогда второе число равно 2 3х, а третье равно 1 (х + 24x). По 4 3 сле соответствующих преобразований получим третье число в виде: 1 (х + 2 х) l 34x — 1 15^ 5 или 1  3 4 3 3 4 4‘  Отвечая на вопрос 6), дети совместно с учителем состав- ляют уравнение х + решают его.4 4 = 80, а затем самостоятельно Учитель наблюдает за работой класса, оказывая помощь тем учащимся, кто испытывает затруднения, выполняя дей- ствия с дробями. 1) х + 24х + 1 1 4 = 80; х (1 + 24 + 14) = 80; 5x = 80; х = 80 : 5; х = 16. (Первое число.) 2) 24х = 24 16 11 16 4 1 44 (Второе число.)   3) 1 = 1 16 =5 16 4 1 = 20 (Третье число.) Далее дети выполняют проверку (16 + 44 + 20 = 80) и при- ступают к самостоятельному выполнению пункта в). Полу- ченные результаты обсуждаются фронтально. В итоге полу- чается такое уравнение: 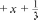 411‘ имеет вид: (•+ ѐі•)80, которое после преобразований 4 11‘ 5  11‘= 80 или 1 9 11 х = 80. №732 рекомендуем использовать для организации са- мостоятельной работы учащихся (1 ряд составляет уравне- ние а), 2 ряд — уравнение 6), а 3 ряд — в)) с последующим фронтальным обсуждением её результатов. №733 выполняется по вариантам (1 вариант — а)), 2 вари- ант — 6)). Для проверки результатов самостоятельной работы полученные уравнения и их решения следует вынести на доску. Шестиклассники обсуждают и корректируют их коллективно. Задача №735 и составленные Мишей и Машей уравне- ния анализируются в классе, а запись решения задачи и её проверку ученики могут выполнить дома. Задачи №736 (а—в) учащиеся решают самостоятельно с последующей проверкой. №737 включает 4 задачи, которые нужно решить, со- ставив уравнение. Опишем возможный вариант организации деятельности учащихся с каждым пунктом этого задания. Работая с пунктом а), шестиклассники самостоятельно читают задачу. Анализируют сначала уравнение, записан- ное Мишей, отвечают на вопрос: «Что обозначил буквой х Миша?› и обосновывают свой ответ. Советуем выполнить в тетрадях записи: х (м2) площадь всей квартиры,   х (м2) площадь одной комнаты.1) х —  х = 50; 2) 70 х = 50;х = 50  х = 70 (м2). = 20 (м2). Ответ: площадь этой комнаты 20 м2. При составлении уравнения ученики ссылаются на ус- ловие задачи. Решив уравнение, они делают вывод, что пло- щадь всей квартиры равна 70 м2. Так как в задаче требуется найти площадь одной комнаты (часть от целого), то нужно 70  (м2g)Затем дети приступают к анализу уравнения, которое за- писала Маша. Как показывает практика, у некоторых ребят оно вызывает трудности. Следует обсудить, как рассуждала  Маша, записывая выражение  х. Возможно, придётся вос- пользоваться схемой, чтобы показать на ней, что х обознача- ет площадь одной комнаты, которая составляет всей квартиры.площади Исходя из этого условия, х (м2) площадь всей квартиры (находим целое по его части). В результате решения уравнения, составленного Машей, получаем х = 20 (м2). Это площадь комнаты.   х 50;3,5x — х = 50; 2,5x = 50; х = 50 : 2,5; х = 20 (м2). Задача №737 (6) читается вслух, и, как показывает прак- тика, ни у кого из учеников не возникает сомнений, что бук- вой х нужно обозначить площадь одной из комнат, площадь второй комнаты будет равна (36 — х). На этом рассуждения учащихся обычно заканчиваются. Вполне возможно, что не- которые шестиклассники, воспользовавшись понятием ‹от- |
