матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb.
|
|
Глава III. ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ Н КОМБИНАТОРИКИ § 19. Множества. Отношения между множествами 4 часа, задания 776-800 В результате изучения темы школьники научатся оперировать на базовом уровне понятиями: ‹множество›, «элемент множества›, «принадлежность», ‹подмножество», «пустое множество›, «конечное множество›, ‹бесконечное множество»; овладеют умениями задавать множества пере- числением их элементов и определять принадлежность эле- ментов числовым множествам. Шестиклассники получат возможность научиться: за- давать множество указанием его характеристического свой- ства, изображать отношения между множествами на кругах Эйлера. УPOK 15. ЗАДАНИЯ 776-781 Lfeль. Познакомить учащихся с понятиями: множество, элемент множества. Создать дидактические условия для фор- мирования у школьников умений определять и записывать принадлежность элементов числовым множествам. Знакомство школьников с понятием «множество› совету- ем начать с беседы о том, что, по мнению учеников, можно назвать множеством. Где и когда они встречали это слово? В каком контексте? А затем перейти к совместному прочте- нию текста учебника в начале § 19. №776 рекомендуем выполнить устно. №777 для домашней работы. Выполняя №778, школьники учатся записывать с по- мощью математических знаков отношение принадлежности. Рекомендуем выполнить это задание в тетрадях и на доске. В результате получаем такие записи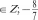:  4,9 & U, 15 3 532 60     4№779 для домашней работы. №780. Школьники работают устно, опираясь на имею- щиеся представления о натуральных и целых числах (конеч- ные множества — А, В, С). Затем дети изображают элементы этих множеств на числовой прямой. №781 — устно. Для ответа на дополнительный вопрос рекомендуем предложить ребятам записать каждое из мно- жеств в соответствующем столбце таблицы.
Затем учащиеся читают новую информацию в учебнике, в которой речь идёт о способе задания множества перечис- лением элементов. На дом: 776, 779. УРОКИ 16, 17. ЗАДАНИЯ 782-794 Lfeль. Формирование у учащихся понятий «конечное множество›, «бесконечное множество›, ‹пустое множе- ство›. Создать дидактические условия для формирования у школьников умений задавать множество перечислением эле- ментов. №782 можно предложить ребятам выполнить самостоя— тельно, а затем проверить фронтально. Важно, чтобы в результате выполнения задания у них по- явился наглядный образец записи множества перечислением элементов с помощью фигурных скобок: а) А—(0, 2, 4, 6, 8};  6) В—11 2 3 41.в) Л = (11, 12, 13, 14};
 При выполнении №784 следует выяснить, в каком слу- чае множество значений переменной х будет конечным (бес— конечным). Запись множества в пункте а) не вызывает у детей за- труднений. Может быть предложена такая запись: Л — (1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11} или такая В— (11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1}. Обе записи верны. (Мно— жество можно обозначить любой буквой, а элементы пере- числить в любом порядке). При записи множества значений переменной в пункте 6), например, fi = (12, 13, 14, 15, ...) (т. е. множество задаётся перечислением элементов), шестиклассники приходят к вы- воду, что перечислить все элементы этого множества невоз- можно, т. к. оно бесконечное. Проблема заключается в поиске нового (другого) способа задания множества. После этого дети выясняют, каким ха- рактеристическим свойством обладают элементы множества D, и выполняют соответствующую запись. {D — множество натуральных чисел, больших 11). Характеристическое свой— ство данного множества включает два свойства, которы- ми обладают все элементы множества fi. (Каждый элемент этого множества: 1) является натуральным числом; 2) боль- ше числа 11. Когда школьники познакомятся с обозначени- ем числовых множеств (на следующем уроке), желательно вернуться к этому заданию и записать характеристическое свойство, используя соответствующую символику: 1) х ш N, х 11. Переменная х обозначает любой элемент данного множества). №785 можно предложить выполнить самостоятельно, а затем организовать фронтальную проверку. Множество прямых, изображённых на рисунке, состоит из элементов: AB,DM, KC, множество лучей — из элементов: OA, OB, OD, ОМ, ОК, ОС. Ученики задают множества перечислением элементов и записывают их, обозначая каждое множество какой-либо буквой латинского алфавита. После этого выяс- няют, в каком множестве элементов больше. №786 — для устной работы. Ученики называют характе- ристические свойства множеств: Амножество натуральных чётных однозначных чисел; В — множество двузначных натуральных чисел, сумма цифр которых равна 5; С — множество двузначных чисел, кратных 6; fi — множество знаков арифметических действий. Затем педагог может предложить детям, работая в парах, составить аналогичные задания и обсудить их коллективно. Перед выполнением задания №788 шестиклассники чита-  ют текст на с. 185 (обозначение числовых множеств). Желательно определить все множества, которым принадлежат данные чис- ла. Такой перебор удобнее оформить на доске в виде таблицы:
Советуем в тетрадях записать утверждения, используя знак принадлежности: а)  Q;6) 17,2 Q,в) 100 Н,‘100 Х,‘100 Q,‘г) —15 Х,‘—15 Q. №789. В процессе самостоятельной работы ученики вы- полняют записи в тетрадях, затем обсуждают их фронтально. Множеству натуральных чисел N принадлежат числа 845 и 36 12’ остальные числа этому множеству не принадлежат (0 g N, 12 15   7 е >)- Для выполнения №790 следует вынести таблицу на доску (интерактивную или обыкновенную) и заполнить её вместе с учениками, комментируя действия. 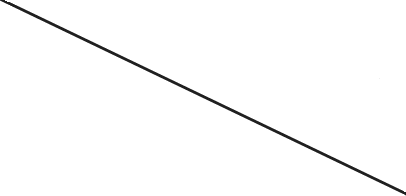 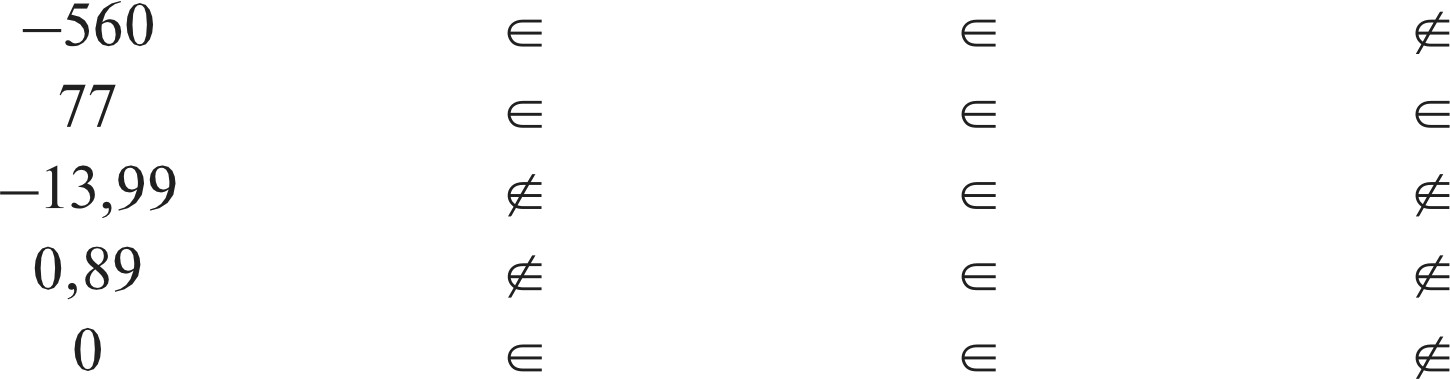 Заполненная таблица имеет вид:
  №791 рекомендуем выполнить в соответствии с указа- нием, данным в учебнике. Ученики чертят и заполняют та- блицу самостоятельно.
   Начать заполнение таблицы можно в классе, а закон- чить дома. Проверить правильность заполнения таблицы желательно при проверке домашнего задания на следующем уроке.При выполнении задания №792 рассуждения учащихся аналогичны рассуждениям в №781. №793 — устно. Важно обсудить каждый из предложен- ных вариантов названия множества и убедиться, что в та- блице записаны элементы множества квадратов двузначных чисел от 10 до 29. №794 — можно предложить выполнить в пapax с после- дующим фронтальным обсуждением. На дом: №783, 787. УPOK 18. ЗАДАНИЯ 795-800 Іfель. Познакомить учащихся с понятием подмножества, отношениями включения и равенства множеств. Создать ди- дактические условия для формирования у школьников уме- ния изображать отношения между множествами с использо- ванием кругов Эйлера. После проверкидомашнего задания рекомендуем приступить к выполнению №795. Цель задания — познакомить ребят с по- нятием «подмножество›. После выполнения этого задания и зна- комства с новой информацией (с. 187) советуем предложить ше- стиклассникам привести примеры множеств и их подмножеств. Вопрос ' для самостоятельного поиска информации из истории математики. №796 можно предложить выполнить в парах, записав элементы каждого множества, и организовать фронтальную проверку. Затем ребята выбирают и обосновывают запись, соответствующую отношению данных множеств {АМ). №797. Ученики выполняют рисунки в тетрадях самосто- ятельно: сначала анализируют запись а) и изображают отно- шение включения множеств с помощью кругов, затем — 6) и т. д. Желательно выслушать комментарии детей в каждом случае. Подводя итог, педагог предлагает такой рисунок на доске: 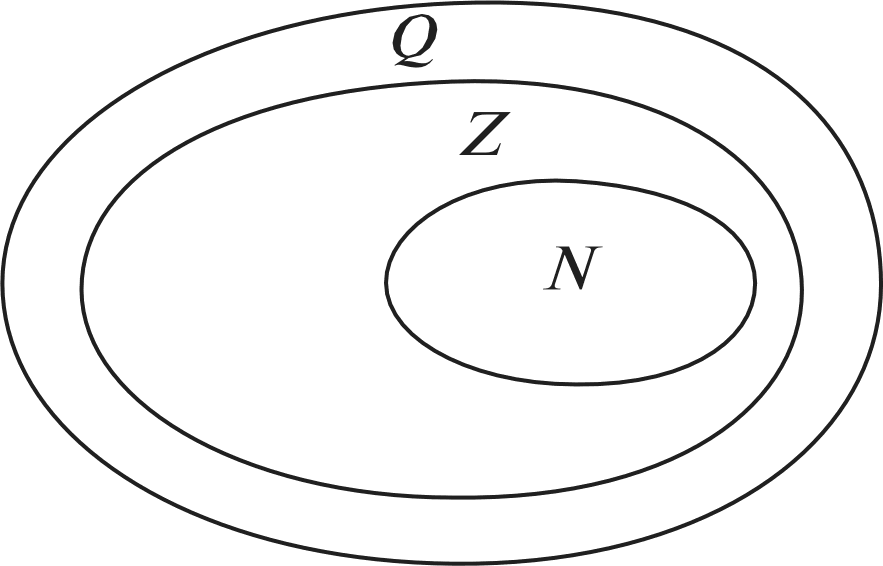  Шестиклассники впервые работают с рисунком, иллю- стрирующим отношения между тремя множествами. В дан- ном случае — отношение включения между множествами на— туральных чисел, целых и рациональных.№798 для домашней работы. №799. Советуем предоставить ученикам возможность самостоятельно ответить на вопрос основного задания. При обсуждении целесообразно зафиксировать все рассуждения в виде записей с использованием знака включения: АВ,АК,АМ,МК,МВ,МА. Анализируя их и выделяя записи: АМ и МА, дети предполагают, что равными являются множества А и М, т.е. множество чисел, оканчивающихся нулём, равно множеству чисел, кратных 10. В заключение дети читают текст под зна- ком «новая информация» (с. 188). №800 — устно: а) и г) — верно; 6) и в) — неверно. На дом: №798. § 20. Операции над множествами 2 часа, задания 801-814 В результате изучения темы школьники овладеют умени- ями находить пересечение, объединение, подмножество чис— ловых множеств в простейших ситуациях. Шестиклассники получат возможность научиться: опре- делять принадлежность элемента объединению и пересече- нию множеств, иллюстрировать пересечение и объединение множеств на кругах Эйлера. УPOK 19. ЗАДАНИЯ 801-807 Іfель. Познакомить учащихся с операциями объединения и пересечения множеств. Создать дидактические условия для формирования у школьников умений находить объединение и пересечение двух множеств в простейших ситуациях. Для проверки домашнего задания (No 798) рекомендуем вынести на доску рисунок. 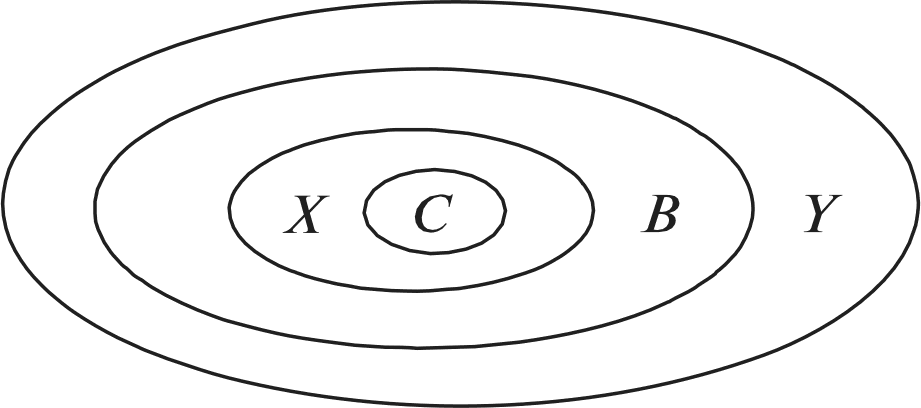 Комментируя рисунок, дети поясняют отношения между данными множествами. №801. Рекомендуем записать на доске множества А,Ви С и ответить на вопрос задания, не открывая учебник. За- тем сравнить выводы учащихся с рассуждениями Маши и Миши. Далее дети читают текст с новой информацией (с. 189) и рассматривают рисунок, наглядно иллюстрирующий опера- цию объединения множеств. №802 — для самостоятельной работы с последующим обсуждением. №804. Знакомство с понятием ‹пересечение множеств» можно организовать аналогично знакомству с понятием «объединение множеств› (см. №801). При выполнении №806 целесообразно не только перечис- лить элементы объединения и пересечения множеств А и В, но и сделать соответствующие записи на доске и в тетради. Они могут выглядеть так: А—(10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29}; В—(20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39}; К=АВ— (10, 11, 12, 13, ..., 37, 38, 39}; М—АВ—(20, 21, 22, 23, 24, 25, 26, 27, 28, 29}. Полезно выполнить рисунок, иллюстрирующий объеди- нение и пересечение множеств А и В(в виде кругов Эйлера), с указанием на нём элементов этих множеств. 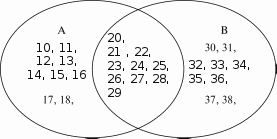 №807. Отвечая на вопросы о числе квадратов и прямо- угольников на рисунке, шестиклассники пользуются учеб- ником. Пока дети работают на местах, педагог выносит на доску рисунок, на котором дети покажут и назовут все ква- драты и прямоугольники (8 квадратов, 18 прямоугольников). Этот же рисунок поможет учащимся обосновать утверж- дения относительно пересечений квадратов и прямоуголь- НикоВ. Для ответа на дополнительный вопрос следует также за- штриховать соответствующие прямоугольники в различных направлениях. Искомая фигура — квадрат (желательно обо- значить его вершины буквами латинского алфавита). АВСD 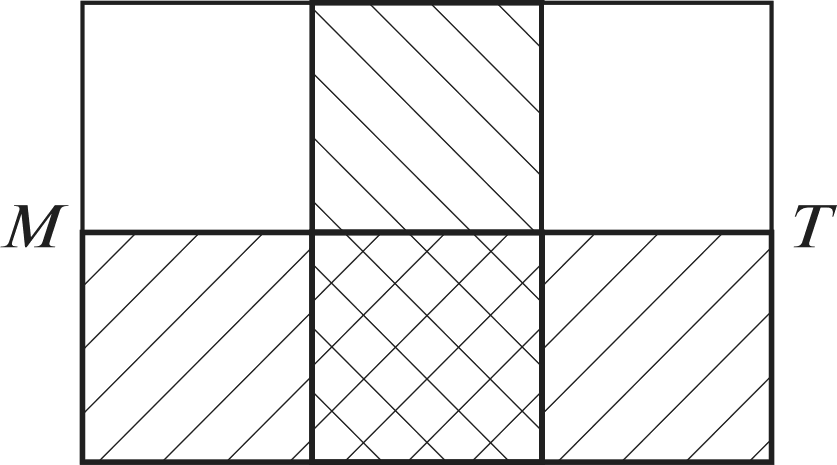   На дом: №803, 805. УPOK 20. ЗАДАНИЯ 808-814 Јfель.Познакомить учащихся со способом решения задач с использованием кругов Эйлера. Для проверки домашнего задания (No 803) советуем вы- нести на доску рисунок. 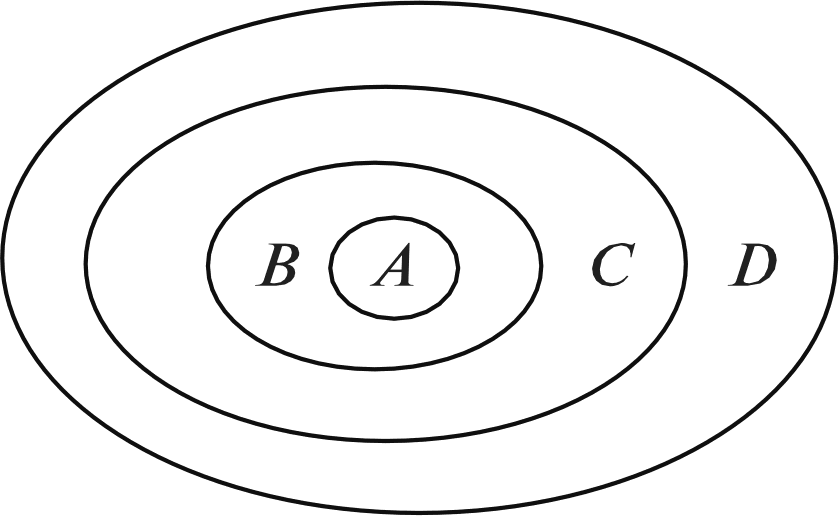 А—множество квадратов, В —множество прямоугольников, С — множество четырёхугольников, Я — множество многоугольников. 200Шестиклассники сравнивают рисунки, выполненные дома, с рисунком на доске, исправляют допущенные ошибки и поясняют неверные записи: СВ,ВА,DС. В №808 шестиклассники впервые используют круги Эй- лера при решении арифметической задачи. После ознакомления с текстом задачи, который выносит- ся на интерактивную доску (учебник закрыт!), желательно дать время учащимся для записи решения задачи. Вполне возможно, что в классе найдутся дети, которые справятся с решением без помощи учителя. Для этого требуется анализ данных в тексте задачи отношений между величинами и со- ответствующие рассуждения. Запись решения имеет вид: 50 — 26 = 24 (с.) — семьи, у которых только автомобиль; 35 — 26 = 9 (с.) — семьи, у которых только мотоцикл; 24 + 9 = 33 (с.) — семьи, у которых только одно транс- портное средство (или автомобиль, или мотоцикл); 33 + 26 = 59 (с.) — семьи, имеющие транспорт; 70 — 59 = 11 (с.) — семьи, не имеющие ни автомобиля, ни мотоцикла. Однако, как показывает практика, большинство ше- стиклассников испытывает затруднения в решении задачи арифметическим способом, поэтому советуем организовать их деятельность в соответствии с диалогом Миши и Маши, чтение которого выполняется вслух (по ролям). В процессе чтения текста Маши, где она предлагает вос- пользоваться кругами Эйлера, учитель или кто-то из ребят на доске выполняет иллюстрацию. Большой круг {В) — мно- жество семей, которые приняли участие в опросе. 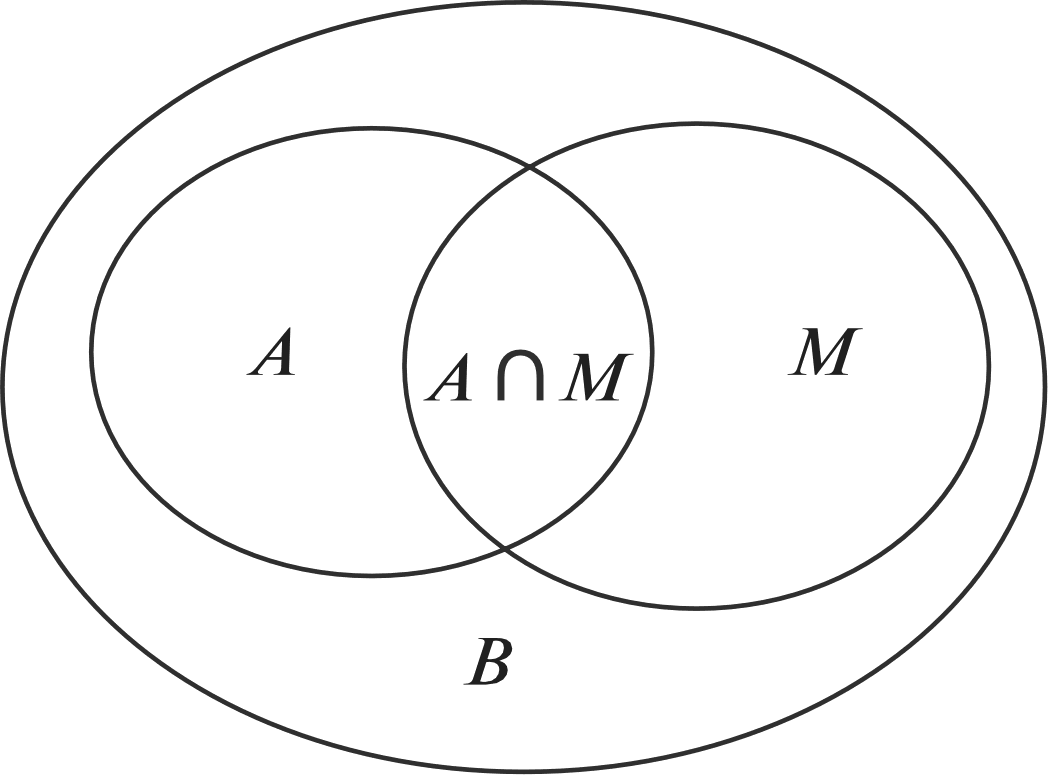 Продолжая работу с рисунком, дети сначала записывают число 26 (количество семей, имеющих и автомобиль, и мото- цикл), а затем, выполняя вычисления в соответствии с рас- суждениями Миши и Маши, вписывают полученные число— вые значения в соответствующие области. 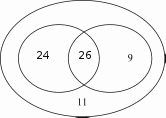 Возможно иначе организовать деятельность учащихся: сначала прочитать рассуждения Миши и Маши и рассмо- треть решение задачи с помощью кругов Эйлера, а затем вы- полнить запись действий с пояснениями. №809 — самостоятельно в тетрадях, а затем коллектив- ная проверка. Рекомендуем предложить детям составить аналогичные за- дачи и проиллюстрировать их решение на кругах Эйлера (рас- смотреть все полученные задачи можно на резервных уроках). В №812 требуется достроить второй угол. Прежде, чем приступить к выполнению задания, желательно вспомнить вместе, что это за геометрическая фигура — угол, из чего он состоит, а из чего состоят те геометрические фигуры, ко- торые должны получиться. Что у них может быть общего? А затем вынести на доску варианты выполнения задания. Обращаем ваше внимание, что задание можно выполнить по—разному. а) пересечением двух углов был луч; пересечением двух углов был треугольник;  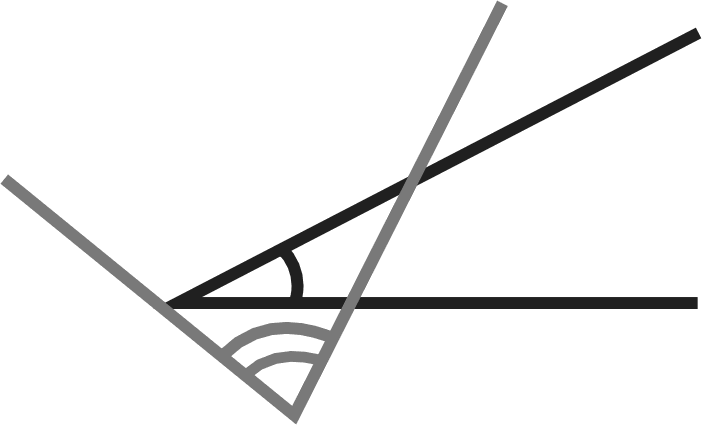 в) пересечением двух углов был четырёх- угольник; 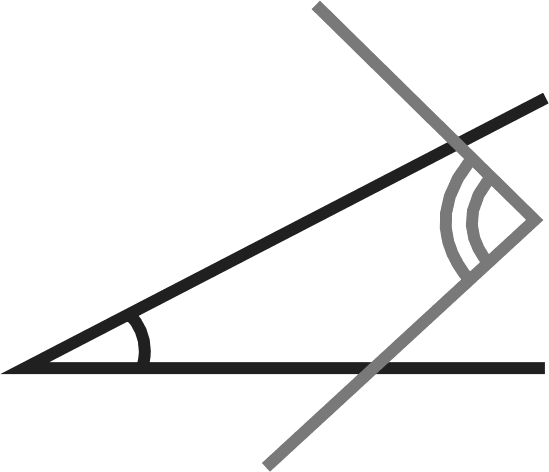 д) пересечением двух углов была точка; г) пересечением двух углов был отрезок; 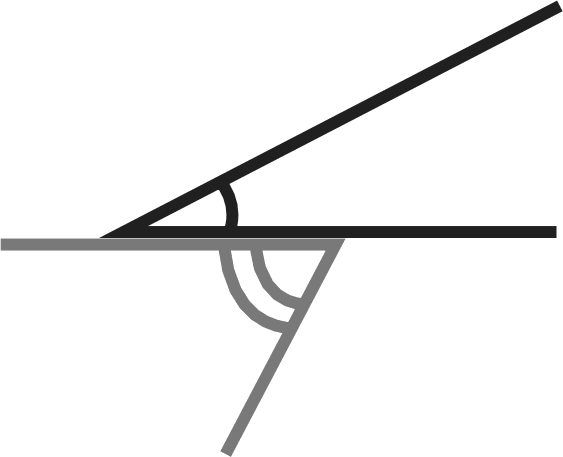 е) пересечением двух углов было пустое множество. 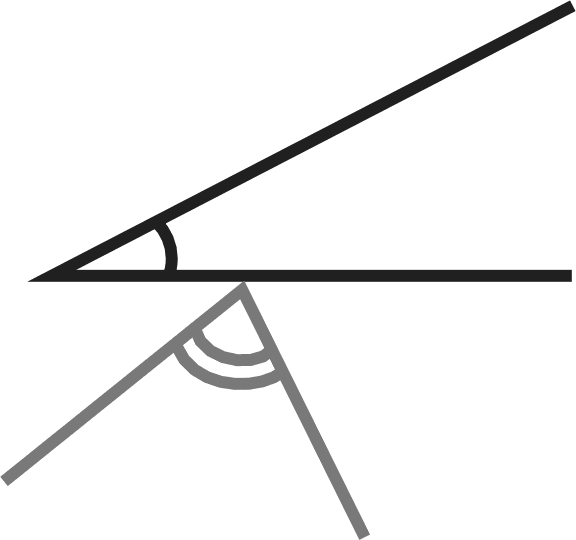 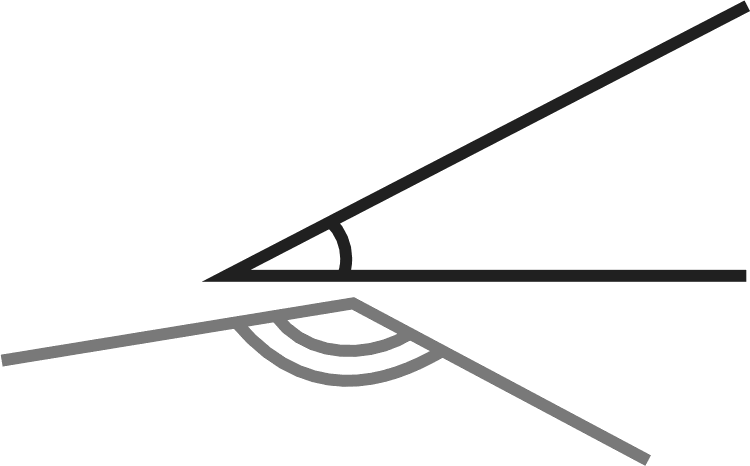 №814* — для работы в пapax. Шестиклассники изобра- жают отношения между данными множествами на кругах Эйлера. Учитель наблюдает за их работой и выносит на до— ску различные варианты рисунков (как верные, так и невер- ные). В ходе обсуждения на доске остаётся рисунок, соответ- ствующий требованию задания: ВА,Ст А,Ст В. 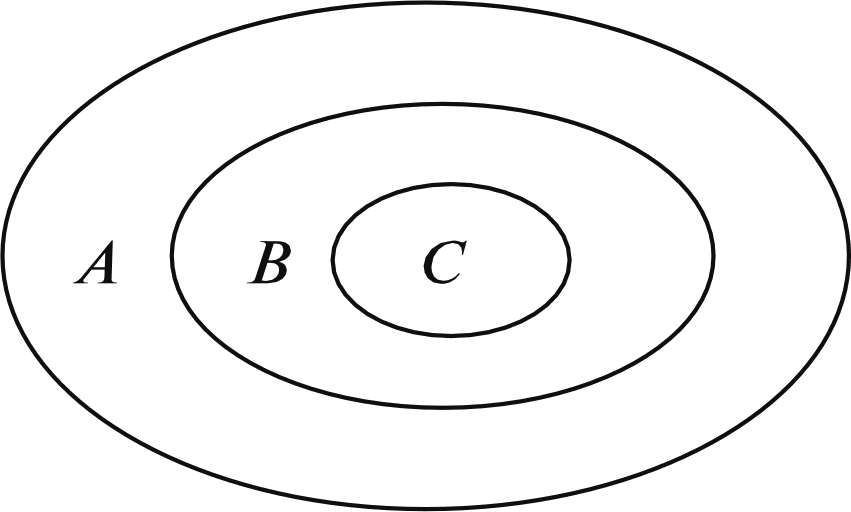 А—множество учеников 6 ‹Б» класса. В—множество учеников, посещающих кружок ‹Нагляд- ная геометрия». С—множество девочек 6 «Б› класса. При ответе на дополнительные вопросы учащиеся обо- сновывают своё мнение. Это могут быть такие утверждения: Все девочки 6 «Б» класса посещают кружок «Нагляд- ная геометрия›, так как множество девочек 6 ‹Б› класса яв- ляется подмножеством множества учеников, посещающих кружок «Наглядная геометрия» {С ш В}. Ученики 6 «А» класса не посещают кружок «Наглядная геометрия», так как множество учеников, посещающих кру- жок ‹Наглядная геометрия» является подмножеством мно- жества учеников 6 ‹Б» класса {ВА). На дом: №810, 811, 813. УPOK 21. КОНТРОЛЬНАЯ РАБОТА № 10 УPOK 22. АНАЛИЗ КОНТРОЛЬНОЙ РАБОТЫ № 10 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
