матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту

• Название: Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
• Анкор: матем метод 6 кл
• Дата: 08.04.2022
• Размер: 2.01 Mb.
• Имя файла: Matem-Metod-6kl_Text (1).docx
• Тип: Методическое пособие; #455623
• страница: 20 из 25

УРОКИ 17-20. ЗАДАНИЯ 574-602

Ifenь. Совершенствовать умения складывать и вычитать ра- циональные числа, записывать данные выражения в виде алге- браической суммы, а также повторитьранее изученный материал. На выполнение №574-602 отводится 4 урока. Ориенти- руясь на указанные номера и методические рекомендации, данные к предшествующим урокам, учитель планирует и ор-

ганизует работу учащихся.

Желательно на одном из уроков выполнить самостоятель- ную работу с последующим фронтальным обсуждением по- лученных результатов, ориентируясь на №569, 570, 572.

Советуем в домашнюю работу включать только те зада- ния (или пункты заданий), которые обсуждались на уроке.

УPOK 21. КОНТРОЛЬНАЯ РАБОТА №6

Ifenь. Проверить: усвоение понятий ‹противоположные числа›, «модуль числа», «алгебраическая сумма»; умения срав- нивать, складывать и вычитать рациональные числа, строить точки с заданными координатами на координатной прямой.
Примерное содержание контрольной работы №6

ВармантI

1. 
   Начерти координатную прямую с единичным отрезком в 2 клетки. Отметь на ней точки, соответствующие: а) |2,5|; 6) |—З|.
   
2. 
   Запиши число 3,7 в виде суммы: а) двух положитель- ных чисел; 6) положительного и отрицательного чисел.
   
3. 
   Запиши данные числа в порядке убывания: 0,4; —1,7; —8; 6,4; —9,2; 13; 9,8; —5.
   
4. 
   Запиши каждое выражение в виде алгебраической суммы и вычисли её значение:
   

а) 5,8 + (—6) + 4 — (—8) + (—1,2);

6) —9 + (—14 + (—1,2) + 4,2 — (—20).

5. 
   Вычисл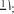и:
   

а) 5,6 — (—1,3); 6) 15 — 21; в) 16 + —

г) —42 — 62; д) —6,7 — 5,3; е) —3 +

6. 
   Найди значение выражения: а) |12,7| — 3,7 + (—2);
   

6) 1,4 |—2| + |—З| |—8|.

7. 
   Реши уравнение:
   

а) 5 х = |—20| = 45; 6) |—З| у = 81.

8. 
   Сравни числа:
   

а) 3,78 ... 3,781; 6) —1,4 ... 0,2;

в) —6,21 ... —8,1; г) 7,583 ... 7,5931.

ВармантМ

1. 
   Начерти координатную прямую с единичным отрез— ком в 3 клетки. Отметь на ней точки, соответствую— щие:
   

а) |3|; 6) —i2 .

2. 
   Запиши число 7,2 в виде суммы: а) двух положи— тельных чисел; 6) положительного и отрицательного чисел.
   
3. 
   Запиши данные числа в порядке убывания: 0,2; —1,4; —9; 5,4; —8,7; 16; 10,7; —6.
   
4. 
   Запиши каждое выражение в виде алгебраической суммы и вычисли её значение:
   

а) 8,5 + (—7) + 9 — (—4) + (—5,6);

6) —10 + (—12 + (—2,1) + 0,1 — (—23).

5. 
   Вычисли:
   

а) 6,5 — (—2,1); 6) 17 — 20; в) 19 + — ;

г) —7 ^{i 1}

2 2

д) —7,6 — 3,4; е) —9 + ⁱ

2

6. 
   Найди значение выражения: а) |—9,3| — 1,2 + |—4|;
   

6) 2,3 |—З| + |—4| - |—5|.

7. 
   Реши уравнение:
   

а) 7 - х = |—12| = 54;

6) |—б| у = 42.

8. 
   Сравни числа:
   

а) 6,21 ... 6,211; 6) —2,5 ... 0,1;

в) —9,43 ... —2,3; г) 4,264 ... 4,2643.
УPOK 22. АНАЛИЗ КОНТРОЛЬНОЙ РАБОТЫ №6

§ 15. Умножение и деление рациональных чисел

10 часов, задания 603-665

В результате изучения темы учащиеся усвоят правила умножения рациональных чисел с одинаковыми и разными знаками, правила деления рациональных чисел с одина- ковыми и разными знаками, правила записи отрицатель- ных обыкновенных дробей; уточнят представления о ра- циональных числах; повторят ранее изученные понятия:

‹противоположные числа›, «модуль», «взаимно обратные числа›, правила умножения и деления обыкновенных и де- сятичных дробей, свойства умножения (переместительное, сочетательное, распределительное), степень числа и др.; приобретут опыт их использования при выполнении раз- личных заданий.
УPOK 23. ЗАДАНИЯ 603-606

Ifenь. Познакомить учащихся с правилами умножения рациональных чисел.

Урок можно начать с самостоятельной работы в фор- ме математического диктанта. Учитель предупреждает, что во время диктанта не нужно выполнять вычисления. Надо только подбирать соответствующие числа и записывать тре- буемые выражения одно под другим, чётко соблюдая нуме- рацию. Ребята нумеруют в тетрадях 10 строчек. Педагог дик- тует: «Запишите выражением:

1. 
   произведение двух натуральных чисел;
   
2. 
   произведение целого отрицательного и целого положи- тельного чисел;
   
3. 
   произведение двух положительных обыкновенных дробей;
   
4. 
   произведение положительной и отрицательной дроби;
   
5. 
   произведение целого положительного числа и числа 1;
   
6. 
   произведение положительной дроби и числа 0;
   
7. 
   произведение целого отрицательного числа и числа 1;
   
8. 
   произведение отрицательной дроби и числа 0;
   
9. 
   произведение двух целых отрицательных чисел;
   
10. 
    произведение двух дробных отрицательных чисел». Результаты математического диктанта проверяются фрон-
    

тально.

Дети читают записанные в тетрадях выражения, неко- торые из них переносятся на доску. Учитель обращается к классу:

— Значения каких выражений мы уже умеем вычислять? Вполне возможно, что некоторые ученики найдут зна- чения во всех десяти пунктах. (Прочитали правило в учеб- нике или узнали об этом у родителей и т. д.) Можно обсу- дить, в каком классе они научились вычислять значения тех или иных выражений. Например: в начальной школе или

в 5 классе.

Какие случаи умножения ещё не рассматривали в школе? Шестиклассники отвечают, на доске обводятся номера 2,

4, 7, 8, 9, 10. Полезно задать и такой вопрос: ‹Как называют- ся числа, которые использовались при записи выражений?» (Рациональные числа.)

• 
  Сегодня мы познакомимся с правилами умножения рациональных чисел, — сообщает педагог.
  

Ребята открывают учебники на с. 134 и читают первое правило: ‹Произведение двух рациональных чисел одного знака положительно, а произведение двух рациональных чи- сел разных знаков — отрицательно›.

Для понимания этого правила следует вернуться к запи- сям на доске, начав с известных детям случаев умножения 1), 3), 5), 6), а затем перейти к случаям 2), 4), 9), 10) и проана- лизировать их с точки зрения прочитанного правила. (Учеб- ники закрыты.)

• 
  Давайте попробуем сформулировать это правило для умножения двух отрицательных чисел, используя понятие
  

«модуль», — предлагает учитель.

В результате обсуждения формулируется правило: ‹Про- изведение двух отрицательных чисел ... и т. д.»

• 
  Теперь попытаемся сформулировать правило ум- ножения чисел с разными знаками, используя понятие
  

t‹MOД ЛЬ».

После обсуждения предложенных формулировок учащи- еся открывают учебник и читают второе и третье правила на с. 134.

• 
  Применим сформулированные правила к вычислению произведений.
  

№604 выполняется устно. Ученики читают выражение, комментируют каждое число в нём и называют результат. Например, а) 8 7, 8 и 7 имеют одинаковые знаки, это целые

положительные (натуральные) числа, перемножаем их, поль- зуясь таблицей умножения, или перемножаем их модули;

в произведении ^{1 . 1}

3 4

первый множитель — положитель-

ное дробное число, второй — отрицательное дробное число. Множители имеют разные знаки, записываем в результа- те знак ‹минус› и перемножаем модули множителей. И т. д. Пункт 6) школьники самостоятельно записывают в тетра- дях, результаты проверяются фронтально.

Аналогично организуется работа с №605. Рекомендуем вынести на доску пункты д) (—2)³ 3² ... 0; и е) (—4)² 2' ... 0, так как они могут вызвать затруднения у детей. При обсужде- нии следует выполнить на доске такие записи: д) (—2) (—2) (—2) 3 3 ... 0; е) (—4) (—4) 2 2 - 2 ... 0, вспомнить опре- деление степени числа (‹Математика», 5 класс; произведе- ние п п а ...а,в котором п множителей, можно записать в виде выражения а") и обратить внимание учащихся на то, что число п может быть как положительным, так и отрица- тельным.

№606 сначала обсуждается фронтально. Дети самостоя- тельно выбирают выражения, соответствующие условию за- дания, и комментируют их. Обычно ни у кого не вызывает сомнения знак в пункте а), так как слева число положитель- ное, а справа — отрицательное.

Все остальные случаи требуют более сложных рассужде- ний. Например, в пункте г) слева и справа получаем отрица- тельные числа, из двух отрицательных чисел больше то, мо- дуль которого меньше, поэтому надо провести рассуждения,

не обращая внимания на знаки: слева число 6 умножают

на , то есть находят ⁱ

2
его часть. Значит, число 6 умень-

шается в 2 раза. Справа это же число 6 увеличивается в 1,5
раза. Отсюда следует, что модуль выражения справа больше, чем модуль выражения слева.

Значит, —68 ¹

2

Аналогичные рассуждения нужно выполнить в пункте е).

В пунктах д) и в) возможно сравнить выражения, пользу- ясь прикидкой результата. Если же ученики испытывают

трудности в проведении рассуждений, они вычисляют зна- чения выражений слева и справа и сравнивают полученные результаты.

На дом: №603, 608.

УPOK 24. ЗАДАНИЯ 607-614

Lfeль. Создать дидактические условия для усвоения ше- стиклассниками правил умножения рациональных чисел и для повторения правил сложения (вычитания) рациональ- ных чисел.

Обращаем внимание учителя на то, что ранее изученный материал учащиеся повторяют в процессе изучения нового. Система заданий, предложенных в учебнике, способствует организации такого повторения.

После фронтальной проверки домашнего задания устно выполняется №609. Советуем напомнить детям о возмож- ности использования переместительного и сочетательного свойств умножения. Например:
а) (—12) (—7) (—4) 5,2 2,5 0; в) —2 (—1,4) (—3,7) (—6) 0.
В случае необходимости можно оформить эти записи на доске.

№610 — для устной работы в парах.

h• 611 (а—в) для письменной самостоятельной работы с последующей фронтальной проверкой.

№612 — для самостоятельного выполнения, после ко- торого полученные результаты комментируются. Например: а) между числами —11 и —7 расположены целые числа —10,

—9, —8.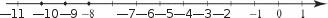




Запись в тетрадях —10 (—9) (—8) = —720.

Из №607 рекомендуем выполнить и обсудить в классе пункты в), е), и).

При выполнении №613 (а,6, г) учащиеся повторяют по- нятия «алгебраическая сумма» и «степень числа». Пояснение может быть таким: а) в скобках дана сумма отрицательных

чисел, поэтому результат — отрицательное число. При умно- жении чисел с одинаковыми знаками получаем положитель- ное число, т.е. произведение будет со знаком +.

По усмотрению учителя значения выражений, записан- ных в неравенстве слева, можно вычислить.

№614 — самостоятельная работа в тетрадях. Варианты выносятся на доску и обсуждаются.

На дом: №611 (r—e), 613 (в, д, е) — вычислить значения выражений.
УPOK 25. ЗАДАНИЯ 615-620

Lfeль. Создать дидактические условия для усвоения ше- стиклассниками правила умножения рациональных чисел и повторения свойств умножения (переместительного, соче- тательного и распределительного).

При выполнении №616 повторяются правила ум- ножения десятичных дробей на 10, 100, сложения чи- сел с разными знаками и сложения отрицательных чисел. Задание выполняется в тетрадях самостоятельно, затем об- суждается. В пункте г) к каждому предыдущему числу при- бавляется —2:

1,4 + (—2) = —0,6; —0,6 + (—2) = —2,6; —2,6 + (—2) = —4,6.

В №617 повторяется правило умножения десятичных дробей на 10, на 100, на 1000. Школьники приобретают опыт умножения чисел с разными и одинаковыми знаками.

№618 учащиеся выполняют в парах, выбирая верные высказывания. В процессе фронтального обсуждения дети обосновывают свой выбор. Например: а) это верное выска- зывание, при обосновании ученики ссылаются на правило:

«Чтобы сложить числа с одинаковыми знаками, надо сло- жить их модули, и перед полученным результатом поставить их общий знак». В пункте д) достаточно привести пример суммы чисел разных знаков, значение которой больше нуля (—2 + 5 = 3, 3 0).

В пункте г) — неверное высказывание, при обосновании ученики ссылаются на правило умножения рациональных чисел разных знаков.

В №619 учащиеся повторяют определения противопо- ложных и обратных чисел. Учитель может дополнить зада- ние, предложив ребятам найти сумму и произведение двух (трёх, четырёх) чисел или разность двух чисел.

На этом же уроке внимание шестиклассников акценти- руется на том, что умножение рациональных чисел облада- ет переместительным, сочетательным и распределительным свойствами (правила на с. 138). Ученики вспоминают фор- мулировку свойств и самостоятельно выполняют в тетрадях

№620 (а, 6) делая необходимые записи и вычисляя значе- ния некоторых выражений по указанию учителя. Эту работу можно продолжить дома.

На дом: №620 (в, г), 607.

УPOK 26. ЗАДАНИЯ 621-626

Іfель. Сформировать умение вычислять значения выра- жений с рациональными числами.

После проверки домашнего задания учитель предлагает детям обсудить №623 в парах, полученные результаты — фронтально. Задание используется для доказательства пере- местительного свойства сложения.

Поэтому желательно будет напомнить учащимся, что знак

«—» (минус) перед числом относится к этому числу, так как при записи числовых выражений мы пользуемся алгебраиче-

СКОЙ С ММОЙ

В тетрадях дети могут сделать такие записи: а) 0,7 — 1,2 = 0,7 + (—1,2) = —1,2 + 0,7;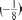

1 1 i ₊ 1

+ —¹ -

4 8 4

е)

8 4

(_ )+

% (—%)(—%)+(— 8 16 8

№624 обсуждается фронтально. Выражение г) выносим на доску —(—(—(—2,3 0,1))). Учащиеся комментируют: про- изведение —2,3 0,1 — отрицательное, перед ним стоит знак

‹—›, значит, надо записать число, ему противоположное, то есть со знаком ‹+». Но перед этим положительным числом стоит минус, значит, противоположное число будет отрица— тельным. А перед этим числом опять стоит «минус›. Значит, результат будет положительным. Ответ: 0,23.

№625, 626 для самостоятельной работы с последующим обсуждением, в котором принимает участие весь класс.

На дом: №621, 622, 623 (6, в, е).

УPOK 27. ЗАДАНИЯ 627-632

Іfель. Познакомить учащихся с правилами деления раци- ональных чисел. Создать дидактические условия для понима- ния и приобретения опыта в вычислении значений выраже- ний, содержащих деление рациональных чисел.

После проверки домашнего задания учитель предлага- ет детям №627. Учащиеся вспоминают правила умножения рациональных чисел. Записывают соответствующие им ра- венства. Можно открыть учебники на с. 134, где приведены эти правила.

Обобщая высказывания детей, учитель напоминает им о том, что разделить число а на число b,значит, найти такое число г, которое при умножении на b даст число а.

Советуем выполнить на доске запись а:b — с и расста- вить соответствующие знаки.

1) а:b— с;3) а :b—с;

2) а :b—с;4) а:b— с.
№628 (a—e) школьники выполняют самостоятельно в тетрадях. Важно обратить их внимание на последователь- ность выполняемых операций:

1. 
   сначала надо определить знак результата;
   
2. 
   затем разделить модуль делимого на модуль делителя. Результаты самостоятельной работы проверяются фрон-
   

тально.

Аналогично организуется деятельность учащихся при вы- полнении №630 (6, в).

После чтения №631 шестиклассники сначала анализи- руют пары выражений, выбирают ответы на поставленный вопрос, затем эти ответы обсуждаются фронтально. Пра- вильные ответы: 1), 3), 4), 5).

Пункт 2) не подходит, т. к. во втором выражении первой и третьей пары делимое больше делителя. Затем ученики анализируют ответы Миши, который записал частное в виде дроби, и ответы Маши, которая считает, что значения вы- ранений в каждой паре одинаковы. Отвечая на вопрос: «Как рассуждала Маша?», учащиеся отмечают, что в первой и вто- рой дробях числители и знаменатели имеют разные знаки,

поэтому перед дробью можно поставить знак минус: —5.

Наиболее трудной для шестиклассников является вторая часть правила на с. 141. Поэтому рекомендуем записать на

доске дробь и, следуя правилу, поменять в ней знаки: а) перед дробью и в числителе, получим ^—5.

6) перед дробью и в знаменателе, получим ⁵

Таким образом,

5

9' 9
—9’

—9‘

Выполнение №632 позволяет выяснить, кто из учащихся понял новое правило. Поэтому лучше, если в этом задании они сначала самостоятельно отметят пары равных дробей. Правильные ответы:

1. 
   Знак поменяли в числителе и знаменателе, дробь не
   

изменилась, значит, ^{7 7}

15 ' —15

2. 
   Знак поменяли перед дробью, в числителе и знамена- теле. Дроби не равны.
   

3. 
   Знак поменяли перед дробью и в числителе:
   
4. 
   Знак поменяли перед дробью ив числителе: —
   

5. 
   Знак пом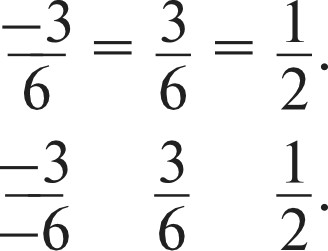еняли в числителе и в знаменателе:
   

5 —5

9' 9

6. 
   Знак поменяли перед дробью, в числителе и в знамена- теле. Дроби не равны.
   

На дом: №628 (ж—к), 629, 630 (а).
УPOK 28. ЗАДАНИЯ 633-639

Јfель.Создать дидактические условия для приобретения детьми опыта в замене знака в отрицательной дроби.

После проверки домашней работы задания а), г), ж), к)

№633 выносятся на доску и обсуждаются фронтально.

Например:

а) 3 + ^—1

7

3 — 26 (знак минус в числителе дроби, его

можно поставить перед дробью, тогда знак действия изменится);

р) 3 + ¹

—7

3 — ¹

7

2 (знак минус в знаменателе дроби,

его можно поставить перед дробью, тогда знак действия из- менится);

7
ж) 6) 3 — ₇ ⁺ ₇ ^{= 1} (знак минус в числителе дроби,

его можно поставить перед дробью, тогда знак действия из- менится);