матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb.
|
|
УPOK 7. ЗАДАНИЯ 48-54 Ifenь.Повторить признаки делимости на 9, на 5, на 3; сравнение натуральных чисел и дробей, сокращение дробей. Над №49 ученики работают самостоятельно, а при про- верке результатов обосновывают свой выбор. Например: а) числа 2 и 3 — взаимно простые, дробь  — несократимая; в) 37 — простое число, поэтому числа 37 и 38 взаимно прос-тые, дробь 37 38 несократимая. При выполнении задания можно повторить определение взаимно обратных чисел, записав дроби: И 2 . 37 38  2 3 38 37’и правило записи неправильной дроби в виде смешанного числа. Полезно также выяснить, почему дробь 72 81 не соот- 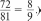 ветствует условию задания. (Она сократимая, её числитель и знаменатель можно сократить на 9;№50. Шестиклассники читают обе задачи, сравнивают, отмечают их сходство и различие, записывают решение за- дач в тетрадях самостоятельно. При проверке полезно обра- титься к схеме. В задаче а) она будет выглядеть так:  0,255 А в задаче 6) — так:  0.225300 т Далее учитель, ориентируясь на №52, предлагает де- тям самостоятельно записать в тетрадях все двузначные числа, кратные 9. При проверке результатов работы учени- ки читают числа и доказывают, что каждое из них делится на 9, ссылаясь на признак делимости. После этого следует открыть учебник и познакомиться с тем, как выполнили за- дание Миша и Маша. Должно получиться 10 чисел. Полезно обсудить и ответ на вопрос, предложенный в конце №51: ‹Сколько можно записать двузначных чисел, кратных числу 3?» (В три раза больше). Проверить это дети могут дома, воспользовавшись способом Миши или Маши. №52 (а) (1-йвариант) и №52 (6) (2-й вариант)учени- ки выполняют самостоятельно по вариантам и затем прове- ряют тетради друг у друга. №54 выполняется устно. Для обоснования ответа учени- ки формулируют признак делимости на 3. Тексты задач №53 сравниваются в классе, а их решения ученики записывают дома. На дом: №48, 52 (в), 53. УPOK 8. ЗАДАНИЯ 55-62 Іfель. Повторить правила сокращения дробей и признаки делимости на 4, на 3, на 9. №55 (а). Ученики читают первую часть задания и отме- чают галочкой числа, вынесенные на доску, которые можно сократить на 4. Учащиеся могут работать в парах, обсуждая варианты ответов и вспоминая признак делимости на 4. (Нуж- но, чтобы числитель и знаменатель были кратны четырём.) Результаты работы проверяются фронтально. Деятель- ность в парах продолжается. Ученики находят дроби, ко- торые можно сократить и на 3, и на 4. Подводится итог, и ребята выполняют записи в тетрадях: сначала сокращают дробь на 4, затем на 3. После этого коллективно обсуждается вопрос: является ли число 12 наибольшим общим делителем числителя и знаменателя этих дробей. №56 выполняется устно. Учитель может дать указание, что при записи трёхзначных чисел, кратных числу 4, следует использовать все данные цифры. Полезно выяснить, сколько трёхзначных чисел можно за- писать тремя данными цифрами, не повторяя их в записи числа. (Шесть.) Над №57 учащиеся работают в парах. Сумма цифр 9, 2, 1 равна 12. Это число кратно трём. Поэтому, переставляя цифры в числе, мы получаем 6 вариантов и ещё три вариан- та: 999, 222 и 111. Эти числа тоже кратны трём. Итого 9 ва- риантов. №58 предназначается также для самостоятельной рабо- ты. Используется признак делимости на 3 и правило сокра- щения дробей. В №59 каждое выбранное учениками утверждение долж- но быть обосновано. Утверждение а) неверное. Для доказательства достаточ- но привести число, кратное трём, которое не кратно числу 9. Например, число 12 кратно трём, но не кратно девяти. Утверждение 6) — верное, так как если число делится на 9, то его можно записать в виде произведения двух множите— лей, одним из которых будет число 9 (п : 9 = b;а— 9 b), но 9 — это 3 3. По свойству делимости произведения, вы- ражение 3 3 а делится на 3. Для доказательства того, что в пункте в) утверждение не- верное так же, как и в а), используется контрпример; г) — ут- верждение верное, достаточно привести пример одного чётно- го числа, которое кратно пяти (30); д) — утверждение верное (например, 30); е) — утверждение верное (например, 729); ж) — утверждение верное, это число 1. В №60 важно обсудить способ действия. Пусть дети сначала напишут дроби самостоятельно, а затем проком- ментируют, как они действовали. Например, можно подо- брать в числителе и знаменателе числа, кратные числу 9 18 27 а можно записать любую дробь, например, основным свойством дроби, получить дробь можно сократить на 9 18 63 , и, пользуясь  которуюСпособы выполнения №61 также могут быть различны- ми. Пусть учащиеся сначала самостоятельно напишут в те- тради число, которое делится на 3 и на 5 (пункт а)). На доску следует выписать 5-6 чисел. Например, число 3375 (сумма цифр делится на 3 и в этом числе последняя цифра 5). Но можно поступить по-другому. Найти произведение 3 и 5 (3 5 = 15) и умножить его на трёхзначное число, чтобы в результате получилось число четырёхзначное. Например, 15 224. (По свойству делимости произведе- ния, это число кратно пяти и трём). 15 224 = 3360 — полу- ченное число удовлетворяет условиям задания. Ученики самостоятельно выполняют №61 (6, в), а пунк- ты (r—e) задаются на дом. В урок можно включить №62 (а, ж, з). Остальные урав- нения этого номера дети решат дома. На дом: №61 (r—e), 62 (6—e). УPOK 9. ЗАДАНИЯ 63-72 Іfель. Повторить свойства делимости суммы, разности, произведения, понятие ‹степень числа›; совершенствовать умение решать задачи. Повторить понятие ‹смежный угол› и его использование при решении задач. При решении задачи №63 рекомендуем использовать схему, обозначив отрезком ABвеличину меньшего из смежных углов.    АВ148°  Так как сумма смежных углов равна 180°, то на один от- резок приходится 180 4 = 45°. Следовательно, один смежный угол равен 45°, другой — 135°. При решении задачи №64 рекомендуем также использо- вать схему. 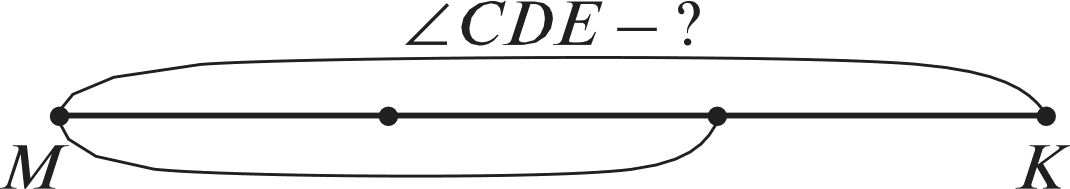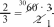Величина угла CDEобозначается отрезком MK,угол ABC   составляет часть углаZABC—60°  На схеме видно, что в задаче надо найти целое по его части. 60 = 90.h•66обсуждается устно. Ответы: а) Можно. Это число 1. 6) Можно. Это само число. в) Можно. Это само число. г) Нельзя. В №67 учащиеся самостоятельно записывают в тетра- дях ряд двузначных чисел 17, 34, 51, 68, 85. После этого мож- но предложить упражнения в сложении двузначных чисел. Например, найти сумму чисел: 17 и 51, 34 и 51, 51 и 68, 34 и 85 и т. д. №68 рекомендуем для работы в пapax. Ученики выби- рают число, которое является корнем уравнения, пользуясь свойством делимости разности (выражение 333 111 — 111333). В данной разности уменьшаемое и вычитаемое кратны трём, поэтому корень уравнения также будет числом, которое крат- но трём. Отсюда следует, что число 11 333 не подходит, т. к. оно не кратно трём; числа 133 333 и 220 778 не подходят, т. к. каждое из них не кратно трём; число 221778 — кратно трём. Значит, х = 221778. Проверка: 333111 221778 111333 J'f• 69(а) шестиклассники выполняют самостоятельно, а потом записывают на доске результаты. Учитель вызывает к доске детей, у которых в тетрадях как верные, так и невер— ные ответы. Правильные ответы: НОД (а, b) — 144; HOK(а, b) — 4320. Если у учащихся возникнут затруднения, они могут вос- пользоваться правилом нахождения HOK нескольких чисел на с. 11 учебника. №70 и №71 рекомендуем выписать на доску и обсудить, записав сначала, чему равен корень уравнения. Например, №70 (а): х — п = b + 15. Чтобы найти умень- шаемое, надо к разности прибавить вычитаемое, получаем х = b + 15 + а.Теперь можно воспользоваться свойством делимости суммы. Все слагаемые по условию делятся на 3, значит, корень уравнения х делится на 3. №70 (6): х — а — b + 182; х = b + 182 + п. Число 182 не делится на 3, значит, сумма не делится на 3. Следовательно, х не делится на 3. Аналогичные рассуждения проводятся и в №71, кото- рый также следует обсудить фронтально, сделав необходи- мые записи на доске. С №72 ученики сначала работают самостоятельно. Они отмечают галочкой уравнения, записанные на доске, корни которых кратны числу 4. Обосновывая свой выбор, дети ссы- лаются на свойства делимости разности, суммы, произведе- ния (формулировки даны на с. 17 учебника). Несколько урав- нений (по усмотрению учителя) учащиеся решают в классе, остальные можно задать на дом. На дом: №65, 69 (6, в), 72 (д, е). УPOK 10. ЗАДАНИЯ 73-81 Іfель. Упражняться в решении уравнений; совершенство- вать умение решать арифметические задачи. Учащиеся работают самостоятельно, учитель оказывает индивидуальную помощь, предлагая карточки со схемами. Например, схема к задаче №74 может выглядеть так: 256,2 м2 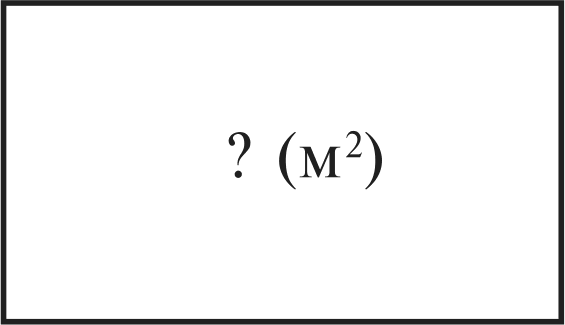 18,3 м   с0,7 от 18,3 м D К задаче №75 — так: ? (м2) 5 от 9,8 м 7 от 9,8 м К задаче №76 можно предложить такую схему:  45 n.К задаче №79: 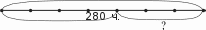 способ 1) 280 : 4 = 70; 2) 70- 7 = 490; 3) 490 — 280 = 210. cnocod 1) 280 : 4 = 70; 2) 70- 3 = 210. №80, 81 рекомендуем выполнить на уроке. Если време- ни на этом уроке не хватит, можно перенести выполнение заданий на следующий урок. На дом: №73, 77, 78. |