матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb.
|
|
ВЫЯСНЯЮТ, ЧТО МОЖНО 3H£tTb, ПОЛЬЗ ЯСЬ ИMeЮЩИMИCЯ ДОН- ными, и какое действие надо для этого выполнить; затем самостоятельно заканчивают запись решения задачи. Таким образом, в первом варианте самостоятельно выполняется только часть решения задачи. Результаты самостоятельной работы затем проверяются фронтально. ВармантМ 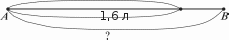 Учащиеся читают задачу и сами записывают её решение. При этом они могут воспользоваться схемами, которые учи- тель заранее нарисовал на доске.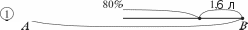 803    Учитель наблюдает за работой класса и предлагает запи- сать на доске решение задачи тем учащимся, которые допу- стили ошибки. Потом эти записи обсуждаются. (Для реше- ния задачи можно использовать схемы и ) ВариантIM Учащиеся читают задачу, самостоятельно рисуют схе- му и записывают решение. После этого работа проверяется фронтально. На дом: № 15, 17. На уроке 3 продолжается работа, начатая на предыду- щем занятии. В классе решаются задачи №21, 22. Деятельность учащихся по решению задач организуется с помощью различных методическмх приёмов: перефор- мулировка текста (замена процентов дробью), постановка новых вопросов к данному условию, выбор схемы, её само— стоятельное построение, обсуждение готового решения, из- менение условия задачи и др. На дом: № 12, 20. УPOK 4. ЗАДАНИЯ 23-29 Іfель. Повторить правило нахождения НОД, сокращение дробей. Совершенствовать умение решать задачи на нахож- дение части (процента) от целого и целого по его части (про- центу). После проверки домашнего задания учитель записывает на доске дробь 208 286 И предлагает учащимся самостоятельно найти наибольшее число, на которое её можно сократить. Возможно, некоторые откроют учебники, другие начнут сами правильно действовать, третьи вообще не поймут во- проса (бывает и такое). Педагогу не следует торопиться с вызовом к доске учени- ка, который сможет объяснить способ действия, или самому переформулировать задание, нацеливая учащихся на нахож- дение НОД. Советуем через 3-4 минуты выяснить, какое же наибольшее число предлагают выбрать шестиклассники для сокращения данной дроби. (Вероятно, это будут разные чис- ла.) Их нужно выписать на доску и после этого приступить к обсуждению способа действия. Рекомендуем также прочитать рассуждения Миши и Маши, которые даны в учебнике (No 23). После этого ребята самостоятельно выполняют задания №23 6), в). (Расклады- вают числитель и знаменатель дроби на простые множители и находят наибольшее число, на которое можно сократить данную дробь.) №24 рекомендуем для устной работы. Чтобы доказать, что дроби сократимые, достаточно назвать число, на кото- poe можно разделить числитель и знаменатель. А чтобы до- казать, что дроби являются несократимыми, необходимо на- звать делители каждого числа и показать, что в числителе и знаменателе взаимно простые числа, то есть их наиболь- ший общий делитель равен 1. Решение задачи №26 учащиеся записывают в тетрадях. Организуя деятельность шестиклассников, учитель может вос- пользоваться рекомендациями, которые даны к урокам 2-3. №25 — в парах, с последующим фронтальным обсуж- дением. Учащиеся комментируют действия Миши и Маши. Маша сначала нашла массу свёклы, которую отправили в ма- газин, а затем ответила на вопрос задачи. А Миша прежде узнал, какую часть свёклы переработали на caxap (1-0,35), а затем нашёл эту часть от массы всей свёклы. Целесообраз- но предложить ученикам выразить 0,35 в процентах и про- читать полученный текст задачи. Запись решения №27 желательно также выполнить в те- тради. (Можно перенести эту задачу на пятый или шестой урок.) №29 обсуждается устно. Решения обеих задач ученики записывают дома. На дом: №28, 29 (а, 6). УPOK 5. ЗАДАНИЯ 30-38 Іfель. Повторить различные способы решения уравне- ний, понятия «двойное неравенство» и ‹координатный луч». №30 обсуждается сначала фронтально. Ученики рас- кладывают числа 222 и 333 на множители: 222 = 2 111 и 333 = 3 111, а число 111 уже разложено на простые множи- тели. Поэтому 222 = 2 - 3 37, 333 = 3 3 37. И т. д. Уравнение из №31 учитель выносит на доску и предлага- ет детям подумать, как записать его решение. Если ученики не могут дать ответ, педагог обращает внимание класса на то, что в данном уравнении 5 2 3 11 х = 2 11 5 первый множитель представлен в виде произведения четырёх чисел (5 2 - 3 11), а результат умножения — трёх чисел (2 11 5). Следовательно, 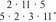 значение х можно записать в виде дроби х =Теперь удобно выполнить сокращение и получить х 1. Возможен и другой способ проверки ответов Миши и Маши. Корень уравнения можно записать вместо х:  5 2 3 11 11 = 5 2 11.Получим произведение, записанное справа. Значит, пра- ва Маша. Решение уравнения 6) 2310 : у = 2 11 3 5 7 из №32 следует обсудить фронтально и записать его на доске: 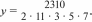 Затем нужно 2310 разложить на простые множители. При подборе делителей ученики повторяют признаки делимости на 2, на 3, на 5 и выполняют запись:
Н н 1 Теперь можно вычислить корень уравнения:   у= 1.Решение уравнений №32 (в, г) шестиклассники самостоя- тельно записывают в тетрадях. При выполнении №33 учащиеся повторяют запись ко- ординат точек, правила сравнения обыкновенных и деся- тичных дробей. Над заданием можно работать устно. Важно, чтобы ученики комментировали способ действия. Например, для случая а), где даны координаты точек Л(5) и В6 , можно неправильную дробь 1 16 записать в виде сме- 3  шанного числа 5 или число 5 представить в виде непра-вильной дроби со знаменателем 3: 5 . Тогда легко ответить на вопрос: левее на координатном луче будет находиться точка, у которой координата меньше. №34 выполняется устно. Дети называют те натуральные числа, которые можно записать вместо х в каждом двойном неравенстве. №35 предназначен для самостоятельной работы. Учени- ки переносят в тетради рисунок из учебника, находят еди- ничный отрезок (2 клетки) и отмечают заданные точки. На дом: №30, 32 (а, д), 36, 37, 38. УPOK 6. ЗАДАНИЯ 39-47 Ifenь. Повторить определение наименьшего общего крат- ного, признаки делимости на 2, на 5, на 3; степень числа. №39 (а) рекомендуем предложить для самостоятель- ной работы в парах. При обсуждении её результатов следует уточнить, как учащиеся действовали (нужно было увеличить каждое число в несколько раз и получить число, кратное данному). Полезно выяснить, можно ли назвать наибольшее число, кратное 308. НЗ Приступая к работе над №40, желательно обсудить, как ученики собираются действовать. Если возникнут трудности, советуем задать вопрос: можно ли сократить каждую дробь? (Для ответа следует обратиться к таблице простых чисел.) Убедившись, что все данные дроби несократимые, ше- стиклассники делают вывод, что для выполнения задания надо воспользоваться основным свойством дроби, то есть умножить числитель и знаменатель на одно и то же число. Например, умножив числитель и знаменатель дроби 226 257 на число 2, получим дробь 514 После такой подготовительной работы дети справятся с этим заданием дома, умножив чис- литель и знаменатель каждой дроби на двузначное число. №41 выполняется устно. Учащиеся сравнивают числа а и b, записанные в виде произведений, и дополняют первое произведение недостающими множителями, то есть находят HOK(п, b).При обсуждении задания следует уделить внимание понятию «степень числа›. (Что означает запись 5’; 52; 2’ и т. д.?) №42, 43(а,6) — для самостоятельной работы. №44 обсуждается фронтально. Ученики повторяют свой- ства делимости суммы (разности) и произведения, признак делимости на 2, определение чётных чисел. Решение уравне- ний можно включить в домашнюю работу. Цель №45 — повторить признак делимости на 3. Учитель может по-разному организовать деятельность учащихся. й вариант. Учебники закрыты. Дети самостоятельно записывают в тетрадях пять трёхзначных чисел, которые делятся на 3. Затем формулируют признак делимости на 3 и читают свои числа. После этого анализируются числа, предложенные Мишей и Машей. й вариант. В этом случае ребята сначала читают за- дание, обсуждают числа, которые записали Миша и Маша. И после этого самостоятельно записывают в тетрадях пять трёхзначных чисел, кратных числу 3. J'f•46 рекомендуем для работы в парах. Учащиеся обсуж- дают те основания классификации, на которые ориентиро- вались персонажи учебника. Миша в одну группу записал правильные дроби, а в другую — неправильные. Маша к од- ной группе отнесла дроби, которые можно сократить на 5, а к другой — те, которые можно сократить на 3. На дом: №39 (6, в), 43 (в, г), 47. |