матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb. Скачать 2.01 Mb.
|
г) з 816. 3 41 31 д) 62 — (0,4)2; е) 1,8 0,001; ж) 6,7 0,01. Реши уравнения: а) Зх — 5,8 = 21,2; 6) 6,01 х = 0,601. Реши задачи: а) В доме 70 однокомнатных квартир, что составля- ет 20% от количества двухкомнатных квартир. На сколько меньше однокомнатных квартир, чем двух- комнатных? 6) Macca гуся составляет 60% от массы кролика. Ка- кова масса гуся, если масса кролика 6,2 кг? Н,епь3.Проверить сформированность умения решать задачи. ВариантI Ширина прямоугольника составляет 0,7 его длины. Найди площадь и периметр прямоугольника, если его длина 7 м. Из двух деревень одновременно навстречу друг дру- гу выехали велосипедист и всадник. Скорость вело- сипедиста 20,5 км/ч, а скорость всадника составляет 0,8 скорости велосипедиста. Они встретились через 2 часа. Какое расстояние между деревнями? От ленты отрезали сначала 8 м, а потом 1 3 оставшейся ленты. Какова была длина ленты, если во второй раз от неё отрезали 6 м? ВариантII Заасфальтировали 18 км дороги, что составило 0,8 всей дороги, которую нужно заасфальтировать. На сколько километров длина заасфальтированной части дороги больше той, которую осталось заасфальтировать? Скорость течения реки составляет 0,2 собственной ско- рости теплохода. С какой скоростью движется теплоход по течению реки, если его скорость в стоячей воде 21 км/ч? Сначала из корзины взяли 13 яблок, а потом 1 7 остав- шихся. Сколько яблок было в корзине первоначально, если во второй раз из неё взяли 6 яблок? УPOK 19. АНАЛИЗ КОНТРОЛЬНОЙ РАБОТЫ №1 Глава 1. ОБЫКНОВЕННЫЕ И ДЕСЯТИЧНЫЕ ДРОБН § 1. Приближённые значения чисел 3 часа, задания 134-145 В результате изучения темы учащиеся получат пред- ставления о приближённом числе, о бесконечной и конеч- ной десятичной дроби; овладеют умениями пользоваться правилами округления чисел для записи их приближённого значения. В 5 классе ребята научились записывать десятичные дро- би в виде суммы разрядных слагаемых, выполнять действия с десятичными дробями (сравнивать, складывать, вычитать, делить и умножать), записывать десятичные дроби в виде обыкновенных (и наоборот), переводить десятичные дроби в проценты (и наоборот). Эти знания и умения можно не только продуктивно по- вторять в процессе изучения темы «Приближённые значения чисел›, но и активно использовать их для усвоения правил округления чисел. УPOK 20. ЗАДАНИЯ 134-136 Ifenь.Познакомить шестиклассников с бесконечными десятичными дробями, с правилами их записи и округления. Ориентируясь на содержание № 134, учитель записывает на доске дроби: 2. 9 . 9 5’ 125 13 и предлагает ученикам самостоя- тельно записать их в виде десятичных дробей. При выполнении задания ребята применяют основное свой- 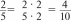 ство дроби = 0,4 и 9 9 8 72 ство дроби = 0,4 и 9 9 8 72 125 125 8 1000 = 0,072 или делят числитель дроби на её знаменатель (2 : 5 = 0,4 и 9 : 125 = 0,072). Учитель приглашает к доске учеников, чтобы они за- 9 125 = 0,072. Проблема возникает с дробью 9 13 Шестиклассники за- мечают, что её знаменатель невозможно привести к зна- менателю вида 10П, т. е. не существует такого числа m, что m 13 = 100 (1000, 10 000 и т. д.) Педагог предлагает выполнить деление ‹уголком» числи- теля данной дроби на её знаменатель. Дети один за другим выходят к доске, каждый записывает по одной операции до тех пор, пока в остатке не получится число 9. Можно вызвать ещё 2-3 учеников к доске, но обычно ребята замечают, что цифры в частном начинают повторяться. Это тот момент, когда целесообразно открыть учебник и прочитать рассуждения Миши и Маши на с. 28, а также новую информацию, которая следует за их диалогом. После этого желательно выяснить, значение какого сло- ва из текста на плашке ребятам непонятно (неизвестно). Как показывает практика, дети называют слово ‹бесконечная›. Учитель обращается к ним с вопросами: Встречались ли вы раньше с этим словом? От какого существительного произошло это слово? (Бесконечность.) Что, по-вашему, означает бесконечность? (Нет конца.) Да, слово ‹бесконечность» используется для характери- стики безграничных, неисчерпаемых явлений (объектов), для которых невозможно указать границы или их количествен- ную меру. Приведите примеры, связанные со словом ‹беско- нечность». (Бесконечное время, бесконечная Вселенная и т. д.) Можно ли назвать самое большое натуральное число? (Нет, обязательно будет следующее, которое больше на 1; на- туральный ряд чисел бесконечен.) Можно ли назвать самое большое двузначное число? Трёхзначное? (Да, можно.) Если выписать все двузначные числа, то этот ряд чи- сел будет конечным или бесконечным? (Конечным.) А ряд трёхзначных чисел конечен или бесконечен? (Конечен.) Какие числа можно записать, используя одну цифру 3? (Какие угодно: 33; 333; 3333... и т. д.) Можем ли мы назвать и записать самое большое число, используя цифру 3? (Нет.) Можно ли, например, назвать и записать самую ма- ленькую дробь, в числителе которой число 1, а в знаменателе число, записанное цифрой 3? На доске появляются записи дробей: 1 . 1 . 1. 1. 1. 1 3 33 333’ 3333 33333’ 33333333 " Педагог предлагает назвать самую большую из данных дробей и самую маленькую, а затем сравнить дроби.  33333333 33333333Можно ли записать дробь, в числителе которой чис- ло 1, а в знаменателе число, записанное цифрой 3, так, что- зззззззз’ бы написанная дробь была меньше 1 (Да, из двух дробей с одинаковым числителем меньше та дробь, знамена- тель которой больше). Несколько учеников выходят к доске и записывают: Десятичные дроби могут быть конечными (0,4; 0,072) и бесконечными. Выполните деление уголком 1 : 3 {1-й ва- риант),1 : 9 {2-йвариант)и вы обнаружите интересный факт. Деление выполняется и в тетрадях, и на доске, и ученики убеждаются в том, что делить можно бесконечно. Что вы заметили? (В частном повторяется одна и та же цифра.) Как можно записать дроби 1 1 И 9 1 3 1 В виде бесконечных десятичных дробей? 3 = 0,3333... = 0,1111... . Затем, используя информацию со с. 31, шестиклассники за- писывают полученные бесконечные десятичные дроби в таком виде: 0,3333... - 0,(3); 0,1111... = 0,(1) и выполняют округление до десятых (0,3333... 0,3; 0,1111... 0,1); до сотых 0,3333... - 0,33; 0,1111... - 0,11; до тысячных 0,3333... = 0,333; 0,1111... = 0,111. №135 ученики обсуждают в парах и самостоятельно вы- ПОЛНЯЮТ. На доску выносятся только те обыкновенные дроби, в ко- торых деление числителя на знаменатель приводит к повто- рению одного и того же остатка. Проведённая работа подводит шестиклассников к выводу о том, каким должен быть знаменатель, чтобы обыкновен- ную дробь можно было записать в виде конечной или бес- конечной десятичной дроби. Этот вывод дети смогут сделать с помощью учителя, ко- торый обратит их внимание на то, что обыкновенные дроби можно разбить на две группы. В ходе беседы ребята отвечают на вопросы педагога (Чем похожи дроби? Чем отличаются?), что помогает им выяснить признак, по которому дроби раз— биваются на группы. На с. 29 приводятся правила, которые следует прочитать только лишь после того, как школьники выскажут свои суждения. В №136 есть указание на способ действия, поэтому школьники могут справиться с заданием самостоятельно. Учащиеся выполняют деление в тетрадях, выписывая на доску результаты, затем округляют их до десятых. На дом: на усмотрение учителя. УРОКИ 21, 22. ЗАДАНИЯ 137-145 Lfeль.Продолжить формировать умения округлять числа и записывать обыкновенные дроби в виде конечных и бес- конечных десятичных дробей. Приступая к выполнению №137, важно обсудить способ действия (нужно числитель разделить на знаменатель). Дети работают в тетрадях самостоятельно и записывают прибли- жённые равенства на доске. Полезно выяснить, чем похожи все записи (дробная часть одинакова), чем отличаются (це- лой частью). Приближённые равенства из № 138 советуем вынести на доску и в ходе беседы выяснить, какие представления об округлении чисел (и их записи) имеют учащиеся. Встречались ли вы с такими записями раньше (5,0; 5,40 и т. д.)? Что показывают нули в записи приближённых чисел? (До какого разряда округлили число.) Фронтальное обсуждение рекомендуем завершить чтени- ем диалога Миши и Маши. №139 (1-й столбец) обсуждается и записывается в те- традях в классе. Второй столбец рекомендуем включить в домашнюю работу. ]ЭИ BЫПOЛHeHИИ • 14(I ШКОЛЬНИКИ ПОЛЬЗ ЮТСЯ СПОСО- бом прикидки, округляя каждую десятичную дробь до це— лых. Эта работа проводится фронтально. Например, в пун- кте а) произведение дробей 3,07 3,2 ученики заменяют выражением 3 3, а произведение дробей 3,81 3,7 заменяют на 4 4 и т. д., что позволяет без особых затруднений выбрать в каждой паре выражение, значение которого меньше 12. Проверка осуществляется с помощью вычислений. №141 выполняется устно. Для обоснования ответа дети ссылаются на правила округления чисел. Задачу № 142 ученики решают самостоятельно. На доску ВЫНОСИТСЯ ТОЛЬКО OTBeT. При выполнении заданий № 143, 144, 145 ученики пользуются правилами округления чисел. На дом: № 139 (2-й столбец), 143 (в), 145 (д—и). § 2. Среднее арифметическое чисел 2 часа, задания 146-155 |
