матем метод 6 кл. Методическое пособие для учителя Пособие предназначено для учителей, работающих по учебнометодическому комплекту
 Скачать 2.01 Mb.
|
Методические рекомендации к урокам математики I ЧЕТВЕРТЬ 45 часов  § 1. Проверь себя! Чему ты научился в пятом классе? 17 часов, задания 1-133 УPOK 1. ЗАДАНИЯ 1-9, 11 Lfeль. Повторить: понятия «правильная дробь›, «непра- вильная дробь», «сокращение дроби», запись обыкновенных дробей в виде десятичных, основное свойство дроби, вза- имно обратные числа, построение углов с помощью транс- портира. На первом уроке необходимо уделить 5-10 минут знаком- ству с учебником. Учащиеся читают названия глав, парагра- фов. Выделяют знакомые и незнакомые понятия. Отмечают, что задания с Мишей и Машей включены в учебник так же, как в 1-5 классах, и в конце учебника дана таблица простых чисел. Разглядывают форзацы. Полезно вспомнить, какие главы включал учебник 5 класса (‹Натуральные числа и нуль», «Обыкновенные дро- би», «Десятичные дроби», «Таблицы и диаграммы») и выяс- нить, почему в названиях глав 6 класса не встречается поня- тие ‹натуральное число». (Любое натуральное число можно записать в виде обыкновенной и десятичной дроби.) 6 = 6 _ 12 _ 42 1 2 7 = 6,0 = 6,00 и т. д. № 1 обсуждается фронтально. Предложенные в задании правила помогают учащимся вспомнить тот материал, кото- рый изучался в 5 классе, и выбрать правило для обоснова- ния ответа. Например, доказывая, что равенство в)  верно,ученики ссылаются на основное свойство дроби (числитель и знаменатель дроби увеличили в 4 раза). Для упражнений в вычислениях уместно предложить увеличить числитель и знаменатель дроби в 5, 6, 7, 3 раза, а также записать полу- ченные дроби в виде натурального числа.  Для доказательства утверждения, что равенство е) 25 = 0,12 является верным, шестиклассники могут воспользоватьсяосновным свойством дроби нить деление 3 : 25 = 0,12. 3 4 12 25 4 100 0,12 или выпол- №2 дети выполняют самостоятельно в тетрадях. При этом способы записи натуральных чисел в виде обыкновен- 2   ных дробей могут быть различными: 9 = 18 , 9 = 9 = 27 9 = И Т.Д. Дроби, данные в №3, учитель выписывает на доску. Каждую десятичную дробь ребята записывают в тетрадях в виде обыкновенной. Затем читают ответы Миши и Маши, анализируют их и отвечают на поставленный вопрос. (Ко— нечно, Миша поступил правильно, он сократил дроби.) Таким образом, в процессе выполнения этого задания учащиеся повторяют не только запись десятичных дробей в виде дробей обыкновенных или в виде смешанных чисел, но и вспоминают правило сокращения дробей. Рекомендуем не спрашивать, какая дробь называется правильной? Неправильной? Кто помнит основное свойство дроби? Какие числа называют простыми? Составными? Луч- ше, если те или иные понятия и определения дети будут по- вторять, выполняя задания. Тогда это действие будет необхо- димым и осознанным. №4 предполагает повторение понятий ‹несократимая дробь» и «правильная дробь›. В классе советуем предложить №4 (6), а №4 (а) задать на дом. В №5 сначала задание выполняется устно. Ученики ком- ментируют записи, сделанные Мишей и Машей. Повторяют основное свойство дроби и алгоритм письменного деления. За- тем записывают в виде десятичной дроби каждое из чисел, ра- ботая в парах. Один действует как Миша, другой — как Маша. №7 выполняется самостоятельно в тетрадях. На доске рекомендуем сделать только одну-две записи. Во время самостоятельной работы не стоит вызывать уче- ников к доске: учитель в случае необходимости окажет ин- дивидуальную помощь. Для проверки самостоятельной ра— боты учащиеся могут обменяться тетрадями. На этом же уроке следует вспомнить, как нужно действо- вать, чтобы записать неправильную дробь в виде смешанного числа. Это можно сделать на доске в процессе коллективной работы, а №6 задать на дом. Вспомнив определение взаимно обратных чисел, шести- классники самостоятельно выполняют в тетрадях №8. № 11 выполняется в соответствии с планом, который дан в учебнике. Отметим, что при выполнении всех заданий дети упраж- няются в устных вычислениях, поэтому вряд ли целесо- образно отводить на данном уроке специальное время для устного счёта. На дом: №4 (а), 6 (любые три дроби), 9. УРОКИ 2, 3. ЗАДАНИЯ 10, 12-22 Lfeль.Повторить: правила нахождения дроби (процента) от целого и целого по его части (проценту), как действовать при построении столбчатой диаграммы. Совершенствовать умение решать задачи. Урок 2 целесообразно начать с №10, в котором учащим- ся предложено сравнить тексты двух задач. Рекомендуем сна- чала выслушать ответы детей, а затем прочитать вслух при- ведённые в учебнике рассуждения Миши и Маши. При выполнении №13 шестиклассники самостоятельно читают задание и выбирают схемы, соответствующие задаче. Результаты самостоятельной работы обсуждаются фронтально (ученики обосновывают выбор схемы). Подходят две нижние схемы, так как отрезокразделён на 10 частей, из которых 7 частей составляют 14 км. Чтобы найти целое (весь путь), надо 14 : 0,7. Работу со схемами можно продолжить, предложив учени-  кам составить задачи к двум верхним схемам. По схеменадо найти число по его части (14 : 0,4), а по схеме — часть от числа (14 0,7). Аналогичная работа проводится с №14. Задачу №16 следует обсудить в классе, так как не все уче- ники смогут самостоятельно сориентироваться в выборе дей- ствий для её решения. Это связано с тем, что число 32 в одном случае следует рассматривать как часть, по которой находится целое (всё количество книг), а в другом случае как целое, от которого находится часть (количество книг во второй коробке). Тем не менее, советуем предоставить всем детям возмож- ность прочитать задачу, обдумать её и начать самостоятельно записывать решение. За отведённое учителем время (не более пяти минут) одни ученики смогут оформить решение задачи полностью, другие напишут одно или два действия. Только после этого рекомендуем приступать к обсуждению задачи. Возможен, например, такой вариант. Учитель записывает 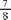 на доске три выражения: 32  ; 32  , 32 и сообщает, что обнаружил в тетрадях различные варианты записи пер- вого действия.Затем педагог предлагает обсудить эти варианты и выяс- нить, какие из них соответствуют условию задачи, а какие не соответствуют. В процессе обсуждения выясняется, что ошиблись те, кто записал выражение 32 4 Для обоснования ответа в № 16 учащиеся могут воспользо- ваться схемой, на которой отрезком ABобозначены все книги, а отрезком АС—книги, которые положили в первую коробку.  32 к.На схеме хорошо видно, что нужно найти целое по его части, то есть количество всех книг, а значит, требуется про- извести деление. Выражение 32 7 8 тоже можно было записать в первом действии и получить ответ на вопрос: ‹Сколько книг поло- жили во вторую коробку?» Здесь также уместно воспользо- ваться схемой, обозначив отрезком AB книги, которые по- ложили в первую коробку.  32 к. В соответствии с условием задачи книги из второй ко-робки составляют коробку. 8 от книг, которые положили в первую Значит, нужно найти часть от целого, то есть выполнить умножение. Учащиеся самостоятельно заканчивают запись решения задачи в тетрадях. Различные способы выполнения третьего и четвёрто- го действий ученики записывают на доске и обосновывают в процессе фронтальной работы.
На этом же уроке обсуждается № 19. Ученики самосто- ятельно читают тексты задач и отвечают на поставленные в них вопросы. Задачу № 18 также лучше выполнить в классе. Приведём возможные варианты организации деятельности учащихся при решении этой задачи. ВармантI Задача читается вслух. На доске заранее нарисованы схемы, на которых отрезком ABобозначен объём кувшина:  80%  803  80%1,6 л 1,6 л  1,6 л Учитель предлагает выбрать схему, которая соответству- ет условию задачи. Это схема . Анализируя её, школьники |