Методическое пособие пм 03 организация занятий по основным общеобразовательным программам дошкольного образования
 Скачать 1.17 Mb. Скачать 1.17 Mb.
|
|
Дидактические игры «Найди звездочку». (Дети делятся на две команды и дают друг другу задания на комбинированный счет. Контроль над правильностью выполнения осуществляется по звездочке, спрятанной под лепестком с соответствующей цифрой.); «Угадай, какие часы идут правильно» (Дети — часы. Хлопают глазками столько раз, какое число показывают контрольные цифровые часы.) и др. Методика ознакомления с принципами построения натурального ряда (задача 3) Предварительная работа После обучения детей счету объектом изучения становятся числа. Дети знакомятся с образованием соседних чисел и их отношениями. Это дает представление о некоторых принципах построения числового ряда. Наглядный материал Множества из одинаковых элементов, различающихся одним признаком (например, цветом или формой). Счетная лесенка.
Возможно использование палочек X. Кюизенера, карточек с цифрами и знаками. Методика обучения С детьми четырех-пяти лет работаем с числами в пределах первого пятка, а с детьми пяти-шести лет работаем с числами второго пятка. Образование соседних чисел (задача 3-а) Фрагмент: Программная задана: показать образование числа 4 и числа 3 друг из друга. Наглядный материал: три круга одного цвета, один — другого. Ход: L Работа с демонстрационным материалом Что это? Сколько? О О О Поставим еще один. О О О • - Сколько стало всего? - Как из трех получилось четыре? - Чтобы получить четыре, надо к трем добавить один. - А как можно из четырех получить три? Чтобы получить три, надо от четырех убрать один. II. Работа с раздаточным материалом Аналогичная работа на другом наглядном материале. Делаем выводы: Чтобы получить последующее число, надо прибавить единицу. Чтобы получить предыдущее число, надо отнять единицу. Замечание: Если дети знают цифры, можно познакомить их со знаками: «плюс» и «минус»: — Чтобы не писать слова, люди придумали знаки: | +1 — «плюс» — значит, прибавить; [ - ] — «минус» — значит, отнять. Можно предложить детям выложить карточками образование 1числа: 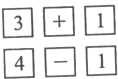 Сравнение соседних чисел (задача З-б) Фрагмент: Программная задача: показать отношение между числами 3 и 4. Наглядный материал: четыре круга, три квадрата расположены так, чтобы прослеживалось приложение. Ход: I. Работа с демонстрационным материалом Что это? О О О О Что это? □ □ □ Чего больше? Чего меньше? Почему? Сколько кругов? Сколько квадратов? — Кругов больше — их 4, квадратов меньше — их 3. Значит, какое число больше? Какое число меньше? II. Работа с раздаточным материалом Аналогичная работа на другом наглядном материале. Делаем выводы: Всегда четыре больше трех, а три меньше четырех. Замечание: Можно дополнить работу заданиями на повторение понятия «поровну» и образования соседних чисел: Как сделать поровну? Сделайте. Как сделали поровну? Кругов и квадратов поровну — их по четыре, значит, четыре равно четырём. Как получилось четыре квадрата? Воспитатель убирает 1 квадрат. Как можно было сделать поровну по-другому? Сделайте. Как получилось три круга? Кругов и квадратов поровну — их по три. Три равно трем. Если дети уже знакомы с цифрами, то можно познакомить их и со знаками: <, >, =. Для этого используем карточки и объясняем: — Чтобы не писать слова, люди придумали знаки: [ > I — «больше» (птичка открывает клювик в сторону большего числа); [<] — «меньше»; | = | — «равно». Можно предложить детям выложить карточками отношения между числами: Усложнения Начинаем с чисел 1 и 2 и постепенно доходим до 9 и 10. Объясняем правило: «Если число называется при счете раньше, то оно меньше. Если число называется при счете позже, то оно больше». Сравниваем числа без наглядности. Используем карточки с цифрами и знаками, затем запись на листе бумаги в клетку (лучше давать в подготовительной группе). Показываем транзитивность отношения «меньше» между числами: «3 < 4, 4 < 5, следовательно 3 < 5» с использованием наглядности (например, «счетной лесенки»). В подготовительной группе даем понятия «больше на ...», «меньше на ...» на основе изучения состава числа из двух меньших чисел. Методика обучения сравнению множеств на основе счета (задача 4) Предварительная работа После изучения способов образования чисел и видов отношений между числами показываем возможности использования счета для сравнения множеств. Методика обучения «Люди придумали счет и числа для своего удобства. Числа мы сравниваем в уме, это быстрее, чем раскладывать предметы парами». Фрагмент: Программная задача: научить сравнивать множества по количеству на основе счета. Наглядный материал: четыре круга, три квадрата расположены так, чтобы не прослеживалось приложение. Ход: I. Работа с демонстрационным материалом Что это? О О О О Что это? □ □ □ Что нужно сделать, чтобы узнать, чего больше, чего меньше? Посчитайте. Сколько кругов? Сколько квадратов? Какое число больше? Какое число меньше? Значит, чего больше? Чего меньше? А как, не считая, проверить? (Способом приложения.) //. Работа с раздаточным материалом Аналогичная работа на другом наглядном материале. Делаем; вывод: Чтобы сравнить, чего больше, а чего меньше, надо посчитать и сравнить числа. Усложнения Увеличиваем количество элементов в сравниваемых множествах от 1 до 10. Постепенно отменяем сравнение множеств приемами наложения и приложения, используя только знание отношений между числами. Методика формирования понимания абстрактности числа (задача 5) Предварительная работа После обучения приемам счета, в процессе формирования счетной деятельности, знакомства с отношениями между числами, сравнения множеств по количеству на основе счета показываем, что число предметов в группе не зависит от их качественных признаков (формы, размера, цвета и др.) и их пространственного расположения. Это помогает детям научиться воспринимать число как абстрактное математическое понятие — количественную характеристику множества, раскрывает закон сохранения количества. Данная работа полезна для развития абстрактного мышления у дошкольников. Методика обучения В процессе практических упражнений с предметами, картинками, геометрическими фигурами показываем независимость числа сначала от размеров предметов, затем от расстояния между предметами, потом от конфигурации их расположения и обсуждаем это. Сначала рассматриваем равночисленные множества, затем неравночисленные. Независимость числа от размера предметов Наглядный материал Одинаковые предметы двух контрастных размеров, расположенные так, чтобы не прослеживалось приложение и действительно казалось, что одних предметов больше, чем других. Фрагмент 1 — Что это ? □ □□ □ □ Чем отличаются? Какие по размеру? Каких квадратов кажется больше? Каких квадратов кажется меньше? Что нужно сделать, чтобы узнать точно? — Посчитайте! По скольку их? Квадратов по пять, значит поровну. Почему мы вначале ошиблись? Больших квадратов кажется больше, маленьких квадратов кажется меньше, но их поровну, потому что по пять. Как, не считая, проверить? (Приложением.) Фрагмент 2 — Что это ? Чем отличаются? Какие по размеру? Каких фигур кажется больше? Каких фигур кажется меньше? Что нужно сделать, чтобы узнать точно? Посчитайте! Какое число больше, 5 или 4? Какое число меньше? Значит, чего больше? Чего меньше? Почему мы вначале ошиблись? Кругов кажется больше, потому что они большие, треугольников кажется меньше, потому что они маленькие. Посчитав, можно узнать точно: кругов меньше, а треугольников больше, потому что 4 < 5, а 5 > 4. • Как, не считая, проверить? (Приложением.) Задание студентам: Напишите самостоятельно схему диалога. Схема: Что это? Чем отличаются? Чего кажется больше? Чего кажется меньше? Как узнать точно? Посчитайте! Какое число больше? Какое число меньше? Значит, чего больше? Чего меньше? Почему мы ошиблись вначале? Как, не считая, проверить? Независимость числа от расстояния между предметами Наглядный материал Две группы предметов одинаковых по величине, расположенных на разном расстоянии («далеко — близко») . Схема Что это? Как расположены? О О О О О Чего кажется больше? Чего кажется меньше? Как узнать точно? Посчитайте! По скольку? По пять — значит, поровну, Почему мы ошиблись вначале? Замечание: нельзя проверять приложением, так как теряется смысл задачи. Независимость числа от формы расположения предметов Наглядный материал Две группы предметов, одинаковых по величине, расположенных по разному (в ряд, по кругу и др.). Например, на рисунке можно выбрать две группы геометрических фигур.  О О О О О Схема Что это? Как расположены? Чего кажется больше? Чего кажется меньше? Как узнать точно? Посчитайте! Какое число больше? Какое число меньше? Значит, чего больше? Чего меньше? Почему мы ошиблись вначале? Усложнения Идем от равночисленных множеств к неравночисленным. Увеличиваем количество элементов в сравниваемых множествах от 1 до 10. Даем сразу несколько отличий. Методика ознакомления с порядковым счетом (задача 6) Предварительная работа После выработки счетных навыков, умения отвечать на вопрос «сколько?» знакомим детей с порядковым счетом, учим отвечать на вопрос «который?». Особенности наглядного материала Множества, состоящие из разных предметов, называемых одним словом (овощи, фрукты, фигуры и т. п.). Методика обучения В средней группе дети считают в пределах первого пятка, в старшей (возможно и раньше) — в пределах десятка. Необходимые знания даются небольшими порциями. В средней группе: Понимание значения порядковых числительных (мотивация использования порядкового счета). Правильное называние и использование порядковых числительных (первый, второй, третий,...). Различение вопросов: «сколько?» и «который?». Понимание различных формулировок вопросов: «который?», «какой по порядку?», «на котором месте?», «какой по счету?». В старшей группе: 5. Понимание словосочетаний: «количественный счет», «порядковый счет». В подготовительной группе: 6. Понимание того, что порядок зависит от направления счета, а количество нет. Фрагмент 1: Программная задача: познакомить с порядковым счетом. Наглядный материал: картинки с овощами. Ход: Что это? Что это?... Как их можно назвать одним словом? Как мы считаем, чтобы ответить на вопрос «сколько?»? Посчитайте! Сколько овощей? Чтобы ответить на вопрос «сколько?», мы считаем так: «Один, два, три, четыре, пять». А чтобы ответить на вопрос «который?», надо считать так: «Первый, второй, третий, четвертый, пятый». Давайте посчитаем вместе! Замечание: воспитатель, называя числительные, показывает на каждую картинку и считает быстро, чтобы счет прозвучал слитно. Называть предметы и согласовывать окончания здесь не надо. Эта работа начнется после выучивания слов-числительных по порядку. Здесь идет хоровое и индивидуальное проговаривание порядкового счета. Затем ответы на различные формулировки вопросов. — Который огурец? — Какой по порядку помидор? - На котором месте лук? Что на пятом месте? Поменяй местами огурец и лук! Который был лук? Который стал? Поставь помидор вторым! Что изменилось? Фрагмент 2: Программная задача: научить различать и понимать словосочетания «количественный счет» и «порядковый счет». Наглядный материал: геометрические фигуры (рис.). Ход: Что это? Что это?... Как их можно назвать одним словом? Что нужно сделать, чтобы узнать, сколько фигур? Посчитайте! Сколько? Когда мы хотим узнать, сколько предметов, то есть их количество, мы считаем так: «Один, два, три...». Это количественный счет, он показывает количество предметов. Повторите хором: «Количественный счет». Индивидуальные вопросы: Посчитай количественным счетом! —- Каким счетом посчитал Миша? А как надо посчитать, чтобы узнать, на каком по порядку месте стоит каждая фигура? Который треугольник? Между которыми по порядку фигурами стоит квадрат? Когда мы хотим узнать, какой по порядку предмет, мы считаем так: «Первый, второй, третий...». Это порядковый счет, он показывает порядок расположения предметов. Повторите хором: «Порядковый счет». Индивидуальные вопросы: Посчитай порядковым счетом! Каким счетом посчитала Маша? Фрагмент 3: Программная задача: показать, что количество предметов не зависит от направления счета (закон «сохранения количества»), а порядок зависит. Наглядный материал: геометрические фигуры (см рис. ). Ход: Что это? Что это? Маша, посчитай количественным счетом слева направо. Сколько? Миша, посчитай количественным счетом справа налево. Сколько? Замечание: дети старшей группы уже могут считать без внешних действий, но здесь мы просим вызванного ребенка посчитать вслух, показывая на предметы. Что можно сказать? Количество предметов не зависит от направления счета. Петя, посчитай порядковым счетом слева направо. Который овал? Оля, посчитай порядковым счетом справа налево. Который теперь овал? А был? А стал? Почему это произошло? Порядковый номер предмета зависит от направления счета. Вопросы на закрепление Как мы считаем, когда хотим ответить на вопрос «сколько?»? Как мы считаем, когда хотим ответить на вопрос «который?»? Как называется счет, которым я считаю? На какой вопрос я отвечаю? Задания на усложнение Отсчитай семь треугольников. Между первым и вторым поставь круг. На котором месте круг? Поставь круг четвертым. Между которыми по порядку треугольниками стоит круг? Дидактические игры «Что изменилось?», «Чего не стало?» (Дети рассматривают ряд предметов и обсуждают их количество и порядок. Дается установка запомнить данную последовательность. Дети закрывают глаза, воспитатель меняет местами или убирает один предмет. Затем обсуждаются вопросы: «Который был? Который стал?». В подготовительной группе можно менять местами или убирать сразу до трех предметов); «Угадай вопрос». (Одному ребенку на ушко задается вопрос или задание, он его выполняет, дети угадывают, о чем его спросили.); «Колобок», «Теремок», «Репка», «На водопой», «12 месяцев». (Обсуждается прочитанная сказка, количество героев, порядок их появления и пр.); «Рассчитайся по порядку». (Подвижная игра, можно проводить на занятиях по физкультуре.); «Магазин». (Сюжетная игра, в процессе которой обсуждается количество товара, порядок в очереди и пр.). | |||||||||||||||||||||||||
