Билеты Навига. Перечень вопросов к зачёту по дисциплине Воздушная навигация и аоп

• Название: Перечень вопросов к зачёту по дисциплине Воздушная навигация и аоп
• Дата: 21.01.2023
• Размер: 5.85 Mb.
• Имя файла: Билеты Навига.docx
• Тип: Документы; #897264
• страница: 2 из 11

3. Системы координат, применяемые в воздушной навигации

1. Географические координаты

Географические координаты — это угловые величины, которые определяют положение данной точки на земной поверхности. Гео­графическими координатами являются широта и долгота места (рис. 1.3).

Широтой места φ называется угол между плоскостью эк­ватора и направлением на дан­ную точку М из центра Земли или длина дуги меридиана, выра­женная в градусах, между эква­тором и параллелью данной точ­ки. Отсчет ведется от экватора к полюсам от 0 до 90°.

Долготой места λ назы­вается двугранный угол между плоскостью начального меридиана и плоскостью меридиана данной точки М или длина дуги экватора, выраженная в градусах, между начальным меридианом и меридианом данной точки. Долгота из­меряется в градусах. Отсчет ведется от начального меридиана к востоку и западу от 0 до 180°.

Меридиан, имеющий долготу 180°, по международному согла­шению принят в качестве линии смены дат и начала междуна­родной разграфки карт.

Долгота места, кроме угловых величин, может измеряться в единицах времени (часах, минутах и секундах).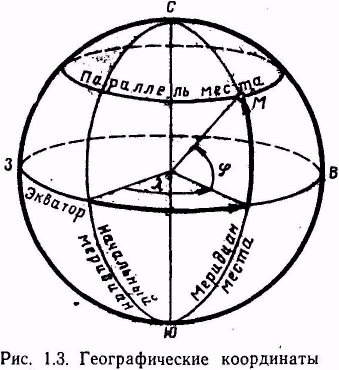



2. Прямоугольные системы координат

Прямоугольные системы координат − это обычные декартовы системы, имеющие три перпендикулярных оси (X, Y, Z). Они используются для описания положения точек в пространстве, на поверхности или внутри Земли.



Если начало прямоугольной системы координат (точка пересечения трех осей) расположено в центре масс Земли, то систему называют геоцентрической, а если в центре аппроксимирующего Землю эллипсоида - референцной.

Системы координат, начало которых находится на поверхности Земли, называют топоцентрическими . Топоцентрические системы используются для определения положения точек на небольшой территории, в пределах которой кривизной Земли можно пренебречь.

В геоцентрических системах координат ось OZ направлена по оси вращения Земли, а в референцных – по малой оси эллипсоида в сторону Северного полюса. Оси ОХ и ОY лежат в плоскости экватора перпендикулярно друг другу.

В зависимости от того, вращается ли система координат вместе с Землей, различают гринвичские и инерциальные системы.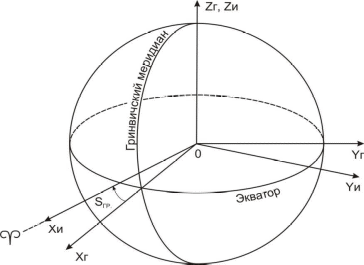



В гринвичскойсистеме координат ось ОХГ лежит в плоскости Гринвичского меридиана и пересекает поверхность Земли в точке с широтой и долготой равными нулю. Такая система координат вращается вместе с Землей, поэтому координаты точек на Земле в течение суток не меняются.

В инерциальнойсистеме координат ось ОХИ направлена в точку весеннего равноденствия на небесной сфере. Это точка, в которой пересекаются небесный экватор и эклиптика. Можно считать, что она занимает фиксированное положение относительно звезд. Поскольку эта система координат фиксирована относительно небесной сферы и вместе с Землей не вращается, координаты точек на вращающейся Земле непрерывно изменяются. Вместе с тем взаимное расположение инерциальной и гринвичской систем может быть точно определено в любой момент времени, поскольку угол между осями OXГ и ОХИ – это гринвичское звездное время (Sгр).

Сферические системы координат

Если Землю представить в виде сферы, то на ней может быть задана сферическая система координат.

Если полюсы сферической системы координат, то есть точки, в которых сходятся меридианы, совпадают с географическими полюсами Земли, то есть точками пересечения оси вращения Земли с ее поверхностью, то такую систему координат называют нормальной сферической.

Координатные линии на сфере задаются с помощью больших кругов.

Большим кругом на любой сфере называется линия, образованная путем сечения сферы плоскостью, проходящей через центр сферы.

Дуга большого круга на земной сфере в навигации называется ортодромией(по-английски – Great Circle) соединяет любые две точки, через которые она проходит, по кратчайшему расстоянию.

Остальные окружности на сфере, плоскости которых не проходят через ее центр, называются малыми кругами.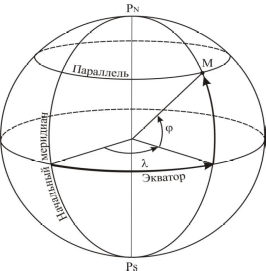



Меридиан – большой круг, плоскость которого проходит через ось вращения Земли. Меридианов бесконечно много, поскольку их можно провести через любую точку.

Экватор – большой круг, плоскость которого перпендикулярна оси вращения Земли. Экватор только один (в конкретной сферической системе координат).

Параллель – дуга малого круга, плоскость которого перпендикулярна оси вращения Земли и, следовательно, параллельна экватору. Сам экватор также является частным случаем параллели.

Сферическая широта φ – это угол между плоскостью экватора и направлением из центра сферы на данную точку.

С 1884 г. в качестве начального меридиана используется так называемый Гринвичский меридиан, вблизи Лондона.

Можно вывести следующие соотношения между координатами точки (φ , λ) в сферической системе координат на сфере радиуса R и координатами (x,y,z) этой же точки в прямоугольной гринвичской системе координат.



Если представить сетку меридианов и параллелей в виде сетки, надетой на глобус (Землю), то ее можно сместить по поверхности сферы и разместить полюсы системы координат (точки схождения меридианов) в любом месте. В таких смещенных системах координат также будут свои широты и долготы, но измеряться они будут с помощью условных меридианов и параллелей.

В картографии такие системы координат называют косыми сферическими, а в навигации – ортодромическими системами координат.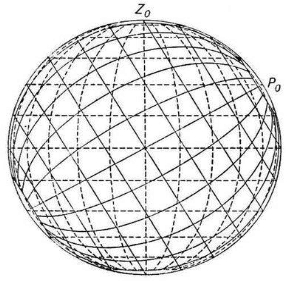



3. Геодезическая система координат СК-42

В 30-е годы ХХ века в Советском Союзе были начаты работы по определению параметров референц-эллипсоида, наилучшим образом подходящего к поверхности геоида на территории СССР. Для этого нужно было провести геодезическую съемку территории страны.

До проведения этих работ в стране не существовало единого, официально принятого реферец-эллипсоида. Для геодезической съемки использовались различные эллипсоиды – Кларка, Хейфорда, Бесселя.

С 1910 г. номинальным исходным пунктом астрономо-геодезических сетей страны является углубление на центральной плитке пола в центре Круглого зала главного здания Пулковской астрономической обсерватории под Санкт-Петербургом. Астрономическая широта этого пункта 59°46'18,71'' , а долгота 30°19'38,40''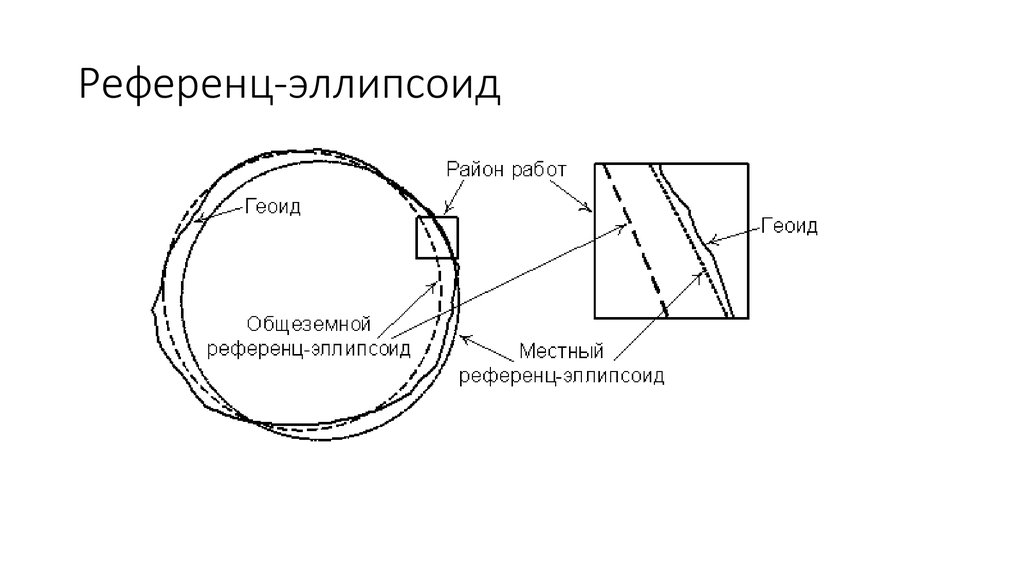



К середине 30-х годов на территории СССР образовались три независимые геодезические системы – Пулковская, Ташкентская и Свободненская.

Они создавались на основе эллипсоида Бесселя 1841 г., но в каждой из систем эллипсоид имел собственную ориентацию. Это приводило к тому, что координаты одной и той же точки в разных системах расходились на сотни метров.

По результатам уравнивания Ф.Н.Красовский предложил принять для земного эллипсоида большую полуось равной 6 378 245 м, а сжатие 1:298,3.

В 1942 г. эти параметры были утверждены. Впоследствии этот эллипсоид получил имя Красовского.

К 1946 г. уравнивание астрономо-геодезической сети было завершено и было принято Постановление Совета Министров СССР № 760 от 7 апреля 1946 г. «О введении единой системы геодезических координат и высот на территории СССР». Этим Постановлением учреждалась «Система координат 1942 г (СК-42)» на эллипсоиде Красовского.

За исходный пункт принималось Пулково, а за исходный уровень отсчета высот – нуль Кронштадтского футштока.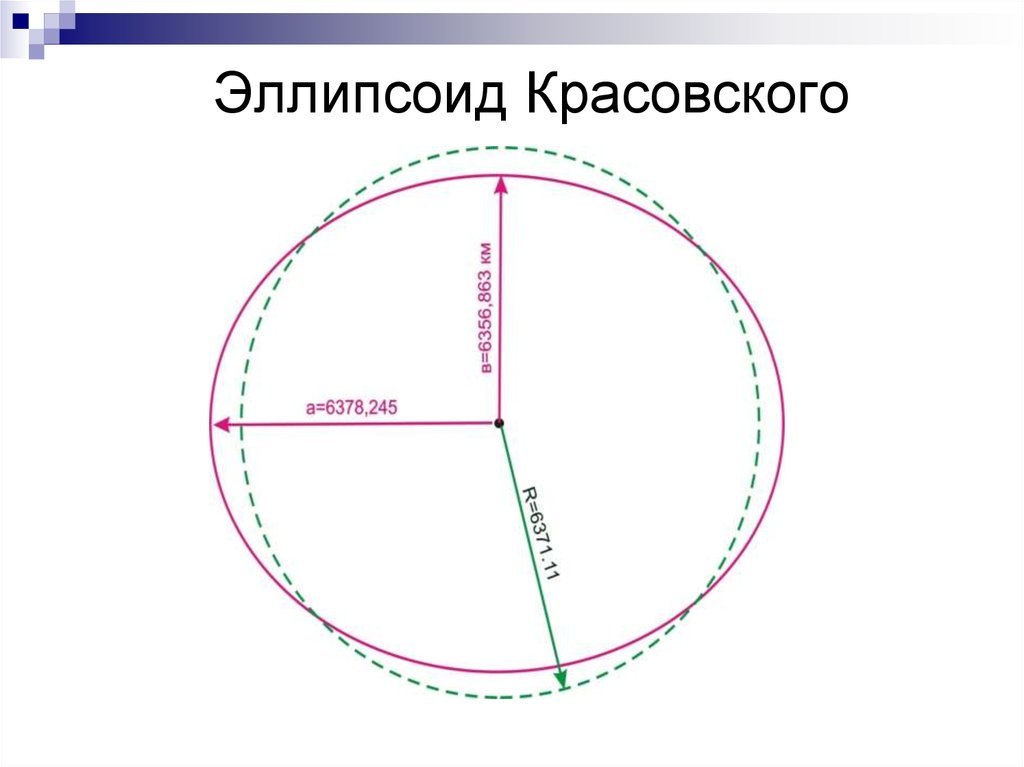



в 1948 г было принято, что исходным пунктом триангуляции СССР является геодезический пункт «Сигнал А» Саблинской сети с координатами

B = 59°46'15,359'' ; L = 30°19'28,318''.  

Азимут с пункта «Сигнал А» на пункт «Бугры»

A = 121°06'42,305''.

Именно в этой геодезической системе координат СК-42 на эллипсоиде Красовского на протяжении десятилетий указываются широты и долготы на картах и в документах аэронавигационной информации нашей страны.

В зарубежной литературе она часто обозначается как Pulkovo 42 или SK-42.

4. Всемирная геодезическая система WGS-84

В соответствии со стандартами ИКАО с 1998 г. все государства – члены ИКАО должны публиковать в документах аэронавигационной информации координаты всех пунктов в общей для всех Всемирной геодезической системе WGS-84 (World Geodetic System). Описание системы и правила ее применения приведены в документе ИКАО

(Doc.9674, WorldGeodeticSystemManual)

WGS-84 представляет собой глобальную отсчетную основу (reference frame), которая в русском переводе документа 9674 названа «глобальной опорной системой». С ее помощью определены:

- прямоугольная система координат;

- эллипсоид, на котором задана геодезическая система координат;

- модель гравитационного поля Земли.

Последовательно создавались такие общеземные системы как WGS-60, WGS-66, WGS-72, WGS-84. Начиная с WGS-66, эти системы включали в себя и мировой геоид, представленный в виде модели гравитационного поля Земли.

WGS-72 разрабатывалась как геодезическая основа первой в мире спутниковой навигационной системы Transit. В качестве общеземного эллипсоида в этой системе использовался эквипотенциальный эллипсоид GRS 67

Министерство обороны США (DoD, Department of Defence) приняло решение о создании собственной системы отсчета (WGS-84), ориентированной на решение военных задач и навигацию по спутниковой навигационной системе Navstar GPS, также финансируемой этим Министерством.

WGS-84 введена в 1987 г.

Благодаря повсеместному использованию Navstar GPS (НавСтар ДжиПиЭс) система WGS-84 получила широкое распространение и установлена ИКАО для международного применения.

Система отсчета (reference system) у WGS-84 в принципе совпадает с ITRS (ITRS точнее привязана к центру масс Земли. Разница между координатами в этих двух системах не превышает 10 см. ),

то есть:

- начало прямоугольной системы координат расположено в центре масс Земли (с учетом массы океанов и атмосферы);

- ось Z направлена на опорный полюс, установленный IERS;

- ось X лежит в плоскости нулевого опорного меридиана, установленного IERS;

- ось Y дополняет систему координат до правосторонней.

• 
  Вследствие такой ориентации ось Z совпадает с направлением на условный земной полюс (Conventional Terrestrial Pole), установленный
  
• 
  Международным бюро времени (BIH) на эпоху 1984 г. с точностью до 0,005'', а ось X с направлением нулевого меридиана BIH с такой же точностью. Ориентация осей не меняется во времени из-за движения земной коры.
  
• 
  Геодезическая система координат WGS-84 задана на эллипсоиде с параметрами:
  

a=6378137,0; 1/α=298,257223563,

• 
  Центр эллипсоида совпадает с началом прямоугольной системы координат.
  

Основные параметры Всемирной геодезической системы WGS-84 приведены в табл.3.1.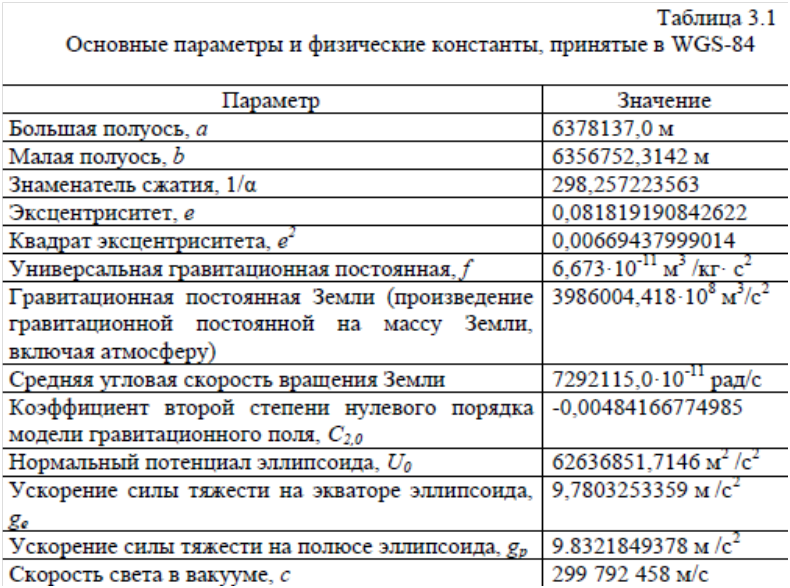



Волна геоида WGS-84 в Пулково составляет +18 м., высота геоида, принятого в России (он проходит через ноль Кронштадтского футштока), над эллипсоидом Красовского составляет в этом же месте +12,8 м.

Различие в высотах в основном вызвано разными эллипсоидами. Но и уровни геоидов несколько различаются.

В нашей стране его уровень определен осреднением уровня Балтийского моря, а геоид WGS-84 установлен значением потенциала, «среднего» для всей планеты.

5. Система геодезических параметров Земли ПЗ-90
(«Параметры Земли-90»)

ПЗ-90 («Параметры Земли-90») является системой отсчета (reference system), которая включает в себя:

- геоцентрическую прямоугольную систему координат (X, Y, Z);

- эллипсоид с заданной на нем системой геодезических координат (B, L, H);

- параметры связи с Международной земной отсчетной основой ITRF 2000 (на эпоху 2000 года);

- модель гравитационного поля Земли.

Система прямоугольных координат ориентирована следующим образом:

- начало координат совмещено с центром масс Земли, включая массы океанов и атмосферы;

- ось Z направлена на условный Северный полюс Земли, как определено Международной службой вращения Земли (International Earth Rotation and Reference Systems Service);

- ось X направлена в точку пересечения плоскости экватора и начального (нулевого) меридиана, установленного Международным бюро времени (Bureau International de l’Heure);

- ось Y дополняет геоцентрическую прямоугольную пространственную систему координат до правой.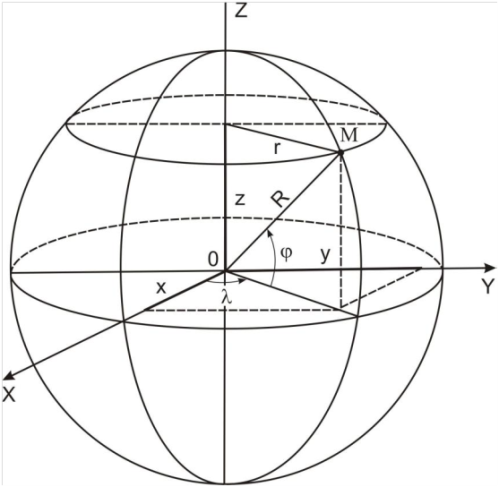

• 
  Можно видеть, что система отсчета ПЗ-90 (соглашение о начале координат, направлении осей) практически совпадает с международной ITRS. Но отличается отсчетная основа (reference frame), то есть набор пунктов на земной поверхности, «закрепляющий» данную систему координат.
  
• 
  Для ITRS, как уже говорилось, такой основой является ITRF, а для ПЗ-90 – пункты космической геодезической сети (КГС) Российской Федерации. Координаты этих пунктов определялись с использованием специальных геодезических спутников ГЕОИК, спутников систем ГЛОНАСС и ЭТАЛОН. (В этой сети 26 пунктов находятся на территории бывшего СССР и еще 7 в Антарктиде).
  

Поскольку набор исходных данных, закрепляющих систему координат, использовался разный, то и системы координат, заданные ПЗ-90 и ITRF, оказались несколько смещенными друг относительно друга

С 2007 года после обработки новых измерений введена очередная версия системы, получившая обозначение ПЗ-90.02.

В этой версии направления осей точно совпадают с WGS-84 (поворота нет), а начало координат сдвинуто по направлениям осей на гораздо меньшую величину (максимум по оси X – 36 см).

Таким образом, системы прямоугольных координат WGS-84, ITRF и ПЗ-90.02 можно считать идентичными с практической точки зрения, то есть даже при решении навигационных задач, требующих высокой точности (например, заход на посадку).

ПЗ-90 включает в себя также эллипсоид, центр которого и направления осей совпадают с центром и направлениями осей прямоугольной системы координат. Этот эллипсоид, так же как в WGS-84, является общеземным эллипсоидом, но параметры эллипсоидов ПЗ-90 и WGS-84 несколько отличаются

В табл.3.2 приведены основные данные, касающиеся ПЗ-90.02.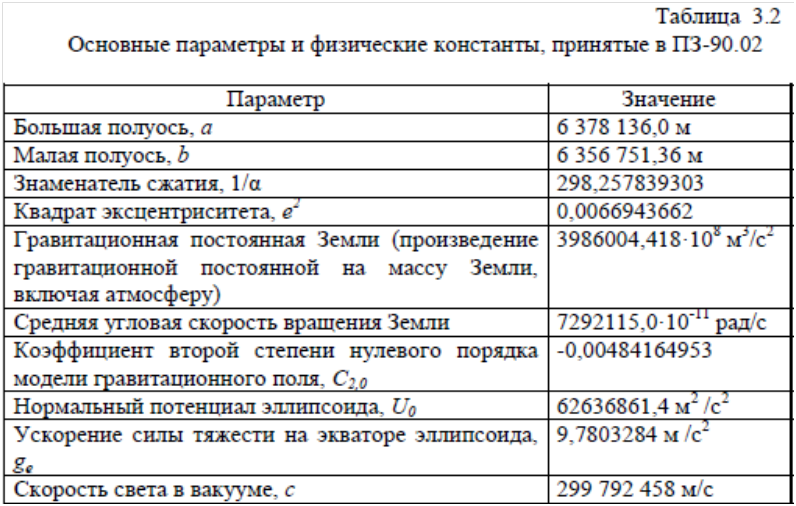