щербакова учебник. Программа Учебники и учебные пособия для педагогических училищ и колледжей
 Скачать 2.02 Mb. Скачать 2.02 Mb.
|
|
§ 1. Развитие счетной деятельности детей седьмого года жизни В работе с детьми седьмого года жизни важное значение имеет дальнейшее развитие счетной деятельности.Они учатсясчитать в пределах десяти в прямом и обратном порядке, количественными и порядковыми числительными,группами подва-три предмета, называя общее количество предметов. Важное место в этой группе занимает счет с участиемразных анализаторов(зрительного,слухового,тактильного,двигательного).Основное внимание уделяется созданию множеств по названному числу. Дети считают звуки,движения, предметы,сопоставляют множества,воспринимаемые разными анализаторами,с заданным числом. Детям седьмого года жизни доступны сложные задания,состоящие из нескольких конкретных заданий. Например,воспитатель предлагает послушать,сколько раз он ударит молоточком,а дети находят среди числовых фигур такую карточку, на которой столько же кружочков или на один больше (меньше),чем количество воспринятых звуков. Используются и такие приемы:«Угадайте,сколько предметов у меня на карточке,если я хлопну в ладоши на один раз меньше (больше)?»Достаточно эффективны дидактические игры и упражнения типа: «Кто знает,пусть дальшепосчитает»,«Назови предыдущее число», «Под какую елочку прыгнул зайчик?»,«Номер дома»и др. Упражнения,связанные со счетной деятельностью,служат основным компонентом каждого занятия по математике.Как правило, на них отводится 3—4мин в начале или в конце занятия. В подготовительной к школе группе важно подвести детей к обобщению, что считать можно,начиная с любого предмета,в любом направлении,основное — не пропустить ни одного элемента и не посчитать один элемент дважды.При этом обращается внимание на направление движения рук и глаз слева направо,сверху вниз.У детей формируются представления о последовательности размещения чисел в натуральном ряду, понимание взаимообратных отношений между числами в пределах десяти, умения пользоваться словами 195 впередиисзадизаданного числа для обозначения этих отношений. Так,воспитатель предлагает детям рассмотреть таблицу, на которой изображены числовые ступеньки(числа от одного до десяти). «Вы хорошо научились считать, — говоритвоспитатель,— знаете числа,а теперь посмотрите на таблицу,на ней в определенном порядке размещены числа. Эта таблица называется числовыми ступеньками(рис. 27). Скажите,какие числа больше, а какие меньше? Сколькоступенек на числовой лесенке? Посчитайте их по порядку.
Я буду показывать ряд, а вы отвечайте,какой он по по рядку.Какое наименьшее число на числовых ступень ках?Какие числа идут пос ле этого? Какое наибольшее число на числовых ступень ках?Какое число в пятом ряду?Какое число опережа ет пять? А еще какие чис ла?Что больше:четыре или пять?Какое число стоит после пяти? Еще какие? Рис.27 Какое число больше:шесть или пять? Посмотрите,какое число перед числом три, а какое —после трех? Чтобольше:восемь или семь? Почему?»Дети разглядывают числовую лесенку, называют числа. Потом воспитатель закрывает лесенку и предлагает вспомнить,какое число больше (меньше),чем названное.На сколько шесть больше пяти? и т.п. Педагог снова открывает лесенку и говорит:«Посчитайте,сколько квадратов в восьмом ряду.Назовите числа,которые предшествуют восьми. Больше или меньше эти числа,чем восемь?Почему вы считаете,что числа девять и десять больше восьми?»Дети отвечают,что эта таблица называется числовой лесенкой.«Правильно,на ней видно,в каком порядке размещены числа, какие числа предшествуют данному числу и какие вдут после него,какие числабольше,а какие меньше». Для закрепления понятия о смежных числах раздаютсякарточки с четырьмя полосками и коробка с кружочками(по двадцать пять кружочков на каждого ребенка).Воспитатель обращается к детям: «Возьмите карточку и посчитайте,сколько на ней полосок. На третью полоску положите шесть 196 кружочков.Какие числа стоят до шести?Какое число стоит перед числом шесть?Что больше:пять или шесть?На какую полоску надо положить пять кружочков?Какое число идет после шести? Что больше:шесть или семь?На какую полоску следует положить семь кружочков?Кто догадался,сколько кружочков надо положить на первую полоску?Положите четыре кружочка. Назовите самое маленькое количество кружочков на вашей карточке.Какие числа идут после семи?» В конце занятия воспитатель делает вывод о том, что всечисла,которые стоят до какого-либо любого числа,меньше,чем это число;числа, которые идут после этого числа,больше его. Понимание отношений между смежными числами натурального ряда позволяет научить считать от любого числа в прямом и обратном порядке. При этом дети сначала могут опираться на демонстрационный и раздаточный материал. Наряду со счетом отдельных предметов,упражнениямив счете их по порядку в этом возрасте вводится обучение счету групп, т.е. обучение счету на основе смены основаниясчета.К этому дети седьмого года жизни уже подготовлены.В частности,обучение измерению и делению целого на равные части является фундаментом,базой для пониманиясчета группами. Начинать ознакомление детей со счетом группами можнос показа практической значимости этой деятельности,экономии времени, установившихся традиций. Так,взрослые считают парами рукавички,носки, обувь;десятками —яйца, иногда овощи, фрукты;набором — мебель(гарнитур), посуду(сервиз) и т.п.Воспитатель подчеркивает,что в такихслучаях несколько предметов воспринимают как единое целое. Опираясь на это, можно предложить детям упражнения со счетом групп разных предметов.Дети создают и считают количество групп, количество предметов в каждой группе,общее количество предметов(сколько всего?). Значение этой работы в том, что вследствие обучения дети осознают связь между счетом и измерением,начинают понимать,что основой(мерой) счета может быть любое число. Т.В.Тарунтаева рекомендует начинать такую работу с анализа двух строений с разными основами(два или три бруска).Потом воспитатель поясняет, что счет также может иметьразную основу. Основа счета — это то,что мы берем за единицу,— это мера. Итак,опираясь на известную детям деятельность,можно ознакомить их с новым видом счета — 197 счетом группами. После этого они считают предметы:прикладывая два кружочка сразу к двум предметам, они называют число один,еще раз прикладывают их и называют число два.Основа счета меняется.Например, за единицу (основу)счета берут три-четыре кружочка. Детей учат создаватьчисло по заданной основе счета. С особым интересом дети воспринимают перегруппирование.Например, из десяти предметов создают пять групп по два предмета в каждой, потом две группы по пять предметов.Вместе с воспитателем они делают вывод о том,что при одном и том же множестве,если уменьшается количествогрупп,то одновременно увеличивается количество предметов в группах. Ребенок поясняет это так: «Сначала у меня было пять групп по два самолета в каждой группе,а потом я каждую группу создал из пяти самолетов,а групп у менястало меньше — всего две». Целенаправленное обучение помогает формировать у детей способность одновременно оценивать все количественные изменения в предметной ситуации. Особое внимание следует уделять при этом развитию речи, умению пояснять, доказывать,аргументировать свой ответ.Важно, чтобы дети умели объяснять путь к достижению цели. Например,они разложили шесть квадратов на две группы,при этом в каждой группе получилось по три квадрата.После этого воспитатель предлагает подумать, как можно из шести квадратовсоздать три группы.Ребенок говорит:«Я из каждой группы возьму по одному квадрату и создам еще одну группу.У меня получится три группы по два квадрата в каждой». Как единица (основа)счета теперь рядом с отдельнымипредметами выступает группа предметов.Это подводит детей к осознанию десятичной системы счисления. Упражнения для самопроверки нумерации десятка образуется число счете цифрой место ряду количественные числом соседними ряда меньших В подготовительной группе большоевнимание уделяется вопросам ... чисел первого.... Дети должны усвоить, как...каждое ...при ... ; как называется каждое число и как оно записывается— ... ; какое ... занимает каждое числов ... от 0 до10; после какого числа и перед каким числом его называют во время счета;какие ... отношения между данным... и ... числами, а также другими числами ...; из каких двух...чисел оно образуется. 198 § 2. Ознакомление детей с составом числа издвух меньших чисел Дети седьмого года жизни учатся определять количественный состав чисел из двух меньших сначала в пределах первой пятерки, а потом в пределах десяти. Эта задача рассматривается как одно из наиболее важных в подготовке детей к вычислительной деятельности. На протяжении всех лет обучения в детском саду в процессе выполнения упражнений с множествами детей постепенно подготавливают к усвоению состава числа из двух меньших чисел. Дети создают множества,объединяют небольшие группы вместе,делят множество на части, сравнивают их между собой.Все эти упражнения способствуют созданию существенной основы вычислительной деятельности.В дальнейшем это будет использоваться как один из приемов сложения (вычитания). Следует подчеркнуть,что основная цель этих упражнений не механическое запоминание таблиц, показывающих,из каких чисел составляется то или другое число, а понимание того, что число,так же как и множество,может бытьобразовано из частей, групп,других чисел,общее количество которых соответствует заданному множеству или числу. Оперируя конкретными множествами и числами, дети осознают отношения частей и целого.Части могут быть равнымиинеравными,большими или меньшими, однако всегда частьменьше целого. Приведем пример такого занятия. Воспитатель ставит цель ознакомить детей с количественным составом числа четыре. «Положите перед собой игрушки, — говорит воспитатель,— посчитайте их. Найдите карточку с соответствующей цифрой и положите ее под игрушками».Дети находяткарточку,воспитатель проверяет, все ли правильно посчитали игрушки и взяли карточку с соответствующей цифрой. «Сколько у вас игрушек?Разложите игрушки на две цветные полоски бумаги».Дети выполняют задание. «Расскажи,Петя,как ты разложил четыре игрушки.Как Алена разложила их? А как разложил игрушки Саша?Как можно составить число четыре?Из каких меньших чисел складываетсячисло четыре?» Детям предлагается собрать игрушки и снова разложитьих на две полосы!,однако уже иначе, не так,как они былиразложены раньше. Задание повторяют трижды. В процессе 199 такого обучения они усваивают, что число четыре составляется из: 3 и 1; 1 и 3; 2 и 2 (рис. 28). 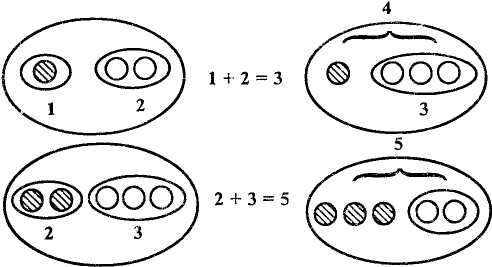 4-3 = 1 5-2 = 3 Рис.28 Дети могут объединить четыре геометрические фигуры из треугольников и четырехугольников, закрасить двумя цветами (всего было четыре фигуры, несколько из них красные, а остальные — зеленые). В качестве наглядности широко используются цифры. Например, дети раскладывают число шесть так: пять и один; четыре и два; три и три; два и четыре; один и шесть. При этом важно, чтобы воспитатель следил за ответами детей, в которых следует называть как все число, так и его части. «У меня было всего пять флажков, из них три флажка я отдал Ирине и два Володе. У Ирины и Володи вместе пять флажков. Итак, число пять можно разложить на три и два». Воспитатель может ставить не конкретные, а проблемные вопросы. Например, на квадратную карточку в один ряд нельзя поставить семь матрешек. Он не дает конкретных указаний, как их разместить, а просто предлагает поставить на карточку семь матрешек. Дети самостоятельно решают разместить их в два ряда. При этом могут быть разные варианты: пять и две; четыре и три; шесть и одна и т.д. Упражнения для самопроверки количественный меньших подготовке вычислительной обучения В этой группе дети учатся определять ... состав чисел из двух ... в пределах десяти. Задача рассматривается как одна из наиболее важных в ... детей к ... деятельности. К пониманию состава числа детей готовят на протяжении всех лет ... в детском выполнения множествами множества делят части упражнения чувственной состава число создать чисел количество саду в процессе ... упражнений с ... . Они создают ..., объединяя небольшие множества вместе, ... их на ... , сравнивают между собой. Эти ... способствуют созданию ... основы для изучения ... числа. Основная цель этих упражнений — понять, что ... , как и множество, можно ... из частей, групп, других ... , общее ... которых соответствует заданному множеству или числу. § 3. Методика ознакомления детей с арифметическими задачами и примерами В обучении решению арифметических задач условно можно выделить два взаимосвязанных этапа: ознакомление со структурой задачи, способами решения ее, и обучение приемам вычислений (А.М.Леушина). При этом дети в значительной степени осознают содержание арифметической задачи, учатся формулировать арифметические действия, аргументировать выбор действия, овладевают приемами сложения и вычитания. Арифметическая задача — это простейшая, сугубо математическая форма отображения реальных ситуаций, которые одновременно близки и понятны детям и с которыми они ежедневно сталкиваются. Есть все основания считать, что это до некоторой степени объясняет достаточно высокий интерес обучающихся к решению арифметических задач. Однако, несмотря на то что вычислительная деятельность вызывает интерес, а самой проблеме отводится значительное место в программе обучения в детском саду, многие старшие дошкольники и даже младшие школьники (учащиеся 1—3-х классов) испытывают значительные трудности именно в решении арифметических задач. Около 20% детей подготовительной группы испытывают трудности в выборе арифметического действия, аргументации его. Эти дети, решая арифметические задачи, в выборе арифметического действия ориентируются в основном на внешние, несущественные, псевдоматематические связи и отношения между числовыми данными в условии задачи, а также между условием и вопросом задачи. Это проявляется прежде всего в непонимании обобщенного содержания понятий: условие, вопрос, действие, а также знаков (+, —, =), в неумении правильно выбрать необходимый знак, арифметическое действие в том случае, 200 201 когда заданное в условии конкретное отображение не соответствовало арифметическому действию (прилетели,добавили, дороже— сложение;улетели, взяли,дешевле —вычитание).Более того,иногда отдельные воспитатели именно на эти псевдоматематические«связи» ориентируют детей. В таких ситуациях вычислительная деятельность формируетсянедостаточно осознанно. Очевидно,основная причина низкого уровня знаний заключается в том, что отличает вычислительнуюдеятельность от счетной. Во время счета ребенок имеетдело с конкретными множествами(предметов,звуков, движений).Он видит, слышит,чувствует эти множества,имеет возможность практически действовать с ними (накладывать,прикладывать,непосредственно сравнивать).Что же касается вычислительной деятельности,то она связана с числами. А числа — это абстрактные понятия. Вычислительная деятельность опирается на разные арифметические действия, которые также являются обобщенными,абстрагированными операциями с множествами. Понимание самой простой арифметической задачи требует анализа ее содержания,выделения ее числовых данных,понимания отношений между ними и , конечно,самих действий,которые должен ребенок выполнить. Дошкольникам особенно трудно понимать вопрос задачи,отражающий математическую сущность действий.Именно вопрос задачи направляет внимание ребенка на отношения между числовыми данными. Обучение дошкольников решению арифметических задач подводит их к пониманию содержания арифметических действий(добавили —сложили, уменьшили— вычли). А этовозможно также на определенном уровне развития аналити-ко-синтетической деятельности ребенка. Для того чтобы ониусвоили элементарные приемы вычислительной деятельности,необходима предварительная работа, направленная на овладение знаниями об отношениях между смежными числами натурального ряда, о составе числа, счете группами и т.д. Особое значение в формировании вычислительной деятельности приобретают четкая системность и поэтапность в работе. Обучение следует начинать с ознакомления со структурой арифметической задачи на основе задач-драматизаций.На одном из занятий воспитатель предлагает выполнить такие действия: «Поставить на стол две автомашины и один самолет».Ребенок выполняет задание, т. е .ставит на стол две 202 машины и один самолет.Воспитатель предлагает детям рассказать о том, что сделал ребенок. Они говорят, что Саша поставил на стол две машины и один самолет. Воспитатель говорит, что к этому маленькому рассказу я добавляю вопрос:сколько всего игрушек Саша поставил на стол? Все считают и отвечают:«Три игрушки». «То,что вы рассказали о действиях Саши, вместе с вопросом,который задала я, называется арифметической задачей.В арифметической задаче есть две части —условие и вопрос».Дети повторяют отдельно условие и вопрос, самисоставляют задачи на основе практических действий. На первых занятиях детям предлагаютсязадачи-д р а -матизации и задачи-и ллюстрации,в которых требуется найти сумму (на основе объединения множеств)или разность(остаток). При составлении таких задачследует идти от малых чисел к большим(до 10). Сначалаодним из числовых данных служит единица. На этих занятиях основное внимание уделяется ознакомлению со структурой задачи, умению детей выделять числовые данные,устанавливать связи между ними, называть и выполнять арифметические действия сложения и вычитания.Посколькурешение в этот период опирается в основном на восприятиеконкретных множеств (предметы,игрушки, картинки),то дети фактически используют счет вместо вычислений.Этот этап в деятельности ребенка закономерный.Однако задачазаключается в том, чтобы научить приемам вычислительнойдеятельности,опираясь на знание отношений между смежными числами натурального ряда, а позднее— количественного состава числа из единиц в пределах десяти. После нескольких упражнений воспитатель дает определение арифметической задаче — это маленький рассказ, в котором есть числа, их не менее чем два, в конце такого рассказа ставится вопрос,который требует определения количества.Вопрос начинается словами «Сколько?»или «На сколько?».Итак, в структуре арифметической задачи ребенок с помощью воспитателя пока еще выделяет только двечасти:условие и вопрос. Ознакомившись со структурой арифметической задачи, дети решают их. С этого момента в массовой практике часто начинается абсолютно свободное составление задач и решение их без учета особенностей,без выделения типов, усложнения их. Принципиально важно ознакомить ребенка с разнымитипами задач, оказать помощь в выявлении специфики, осо- 203 бенностей каждого типа.Именно это вооружает ребенка обобщенными способами умственной деятельности,на что в дальнейшем можно будет опереться при изучении математики в школе. В системе дальнейшей работы можно выделить несколько этапов в зависимости от типов арифметических задач. Следует подчеркнуть,что термин«типы задач»в работе с детьми не используется,а употребляются такие слова и выражения:подобные,такие же самые,новые, совсем другие;сравните задачи, которые мы решали на прошлых занятиях,с этими задачами»и т.п. Первый этап в работе заключается в составлении и решениизадач на нахождение суммы и остатка.На этом этапеважно показать детям,как изменяется множество при объединении или вычитании частей. Ход рассуждений сначала может идти от условия к вопросу задачи.Например: «К кормушке прилетели сначала три птички, потом— еще одна. Сколько всего стало птичек?» Дети вместе с воспитателемрассуждают так: было три птички, потом прилетела еще одна, теперь их стало на одну больше.Эту задачу можно решитьсложением(к трем прибавить один). Делается вывод: к кормушке прилетели четыре птички. «В магазине было пять телевизоров,один из них продали. Сколько телевизоров осталось в магазине?»Решая эту задачу,воспитатель учит аргументировать свои действия так: было пять телевизоров,один продали,следовательно,их осталосьна один меньше.Чтобы узнать,сколько телевизоров осталось,нужно от пяти отнять один и получится четыре. Воспитатель формирует представления о действиях сложения и вычитания,одновременно знакомит их со знаками «+»(прибавить,сложить), «—»(отнять, вычесть)и «=» (равно,получится). Таким образом, ребенок постепенно от действий с конкретными множествами переходит к действиям с числами — решает арифметическую задачу. Уже на втором-третьем занятии наряду с задачами-дра-матизациями и задачами-иллюстрациями можно предлагатьдетям решать устные(текстовые)задачи. Этот этап работы тесно связан с использованием карточек с цифрами и знаками.Особенно полезны упражнения в самостоятельномсоставлении аналогичных задач. При этом воспитатель должен помнить,что основное заключается в нахождении не столькоответа(названия числа),сколько в нахождении пути решения.Так, дети решают задачу. «На участке детского сада в пер- 204 вый день посадили четыре дерева,а на следующий— еще одно дерево. Сколько деревьев посадили за два дня?»Воспитатель учит ребенка мыслить во время решения задачи. Онспрашивает:«О чем идет речь в задаче?»— «О том, что на площадке детского сада посадили деревья».«Сколько деревьевпосадили в первый день?»— «Четыре». —«Сколько деревьевпосадили во второй день?»— «Одно дерево».— «А что спрашивается в задаче?» «Сколько всего деревьев посадили на участке за два дня?» —«Как можно узнать, сколько деревьев посадили на участке?»— «К четырем прибавить один». Воспитатель подводит детей к такому обобщению:чтобы к числу прибавить один (единицу),не надо пересчитыватьвсе предметы, надо просто назвать следующее число. Когдак четырем прибавляем один, мы просто называем следующее за числом четыре число пять. А когда надо вычесть, отнять один — следует назвать предыдущее число, стоящееперед ним. Предлагаем несколько задачпервого типа.
Если с первых шагов обучения дети осознают необходимость,значение анализа простых задач,то позднее этопоможет им в решении сложных математических задач. Активность умственной деятельности ребенка во многом зависит от умения воспитателя ставить вопросы,побуждать его мыслить. Так,воспитатель спрашивает у детей: «О чемследует узнать в задаче?Как можно ответить на вопрос? Почему ты считаешь,что надо сложить?Как ты прибавишь к четырем единицу?» Следующий этап в работе связан с ознакомлением детей с новыми задачами:на отношениябольше(меньше) на несколько единиц. В этих задачах арифметические действия какбы подсказаны в самом условии задачи. Отношение«больше на единицу» требует от ребенка увеличения,присчитывания,сложения. Выражение«больше (меньше)на единицу»дети усваивают при сравнении смежных чисел.При этом акцентировать внимание на отдельных словах больше,меньше и ориентировать их на выбор арифметического действия 205 только в зависимости от этих слов не рекомендуется.Позднее при решении«не прямых,косвенных»задач возникает потребность переучивать,а это намного сложнее, чем научить правильно делать выбор арифметического действия. Предлагаем несколько задачвторого типа.
В группе детей седьмого года жизни в начале работы воспитатель предлагает только прямые задачи, в них вопрос как бы подсказывает,какое действие следует выполнить— сложение или вычитание. Шестилеткам необходимо предлагать сравнивать задачи разных типов, хотя это для них довольно сложное дело,поскольку они не видят текста, а обе задачи необходимоудерживать в памяти. Основным критерием сравнения является вопрос. В вопросе подчеркивается,что нужно определить только количество второго множества,которое больше(меньше)на один, или общее количество(остаток, разницу).Арифметические действия одинаковые,а цель разная,что способствует развитию мышления.Воспитатель постепенно подводит детей к пониманию этого. Еще более важный и ответственный этап в обучениидетей решению арифметических задач — ознакомление их с третьим типом задач на разностное сравнение чисел. Задачи этого типа решаются только вычитанием.При ознакомлении с этим типом задач внимание обращается на основное— вопрос в задаче.Вопрос начинается со слов «насколько?»,т.е. всегда необходимо определить разницу, разностные отношения между числовыми данными. Воспитатель учит детей понимать отношения зависимости между числовыми данными. Анализ задачи должен быть более детальным.Во время анализа дети должны идти от вопроса к условию задачи. Следует объяснить, что в выборе арифметического действия основным всегда является вопрос задачи,от его содержания и формулировки зависит решение.Поэтому следует начинать с анализа вопроса.Сначала детям предлагают задачу без вопроса. Например:«На прогулку дети взя- 206 ли четыре больших мяча и один маленький. Что это такое? Можно ли это назвать арифметической задачей?» —спрашивает воспитатель.«Нет, это только условие задачи»,— отвечают дети. «А теперь поставьте сами вопрос к этой задаче». Следует подвести к тому, что к условию этой задачи можно поставить два вопроса:сколько всего мячей взяли на прогулку?На сколько больше взяли больших мячей,чем маленьких?В соответствии с первым вопросом следует выполнитьсложение,а в соответствии со вторым —вычитание. Это убеждает в том, что аначиз задачи следует начинать с вопроса. Ход рассуждений может быть таким: чтобы узнать, скольковсего мячей взяли на прогулку,надо знать,сколько взялибольших и маленьких отдельно и найти общее их количество.Во втором случае надо найти, на сколько больше одних мячей,чем других,т.е. определить разницу. Разницу всегда находят вычитанием:от большего числа вычитают меньшее. Итак,задачи третьего типа помогают воспитателю закрепить знания о структуре задачи и способствуют развитию умения различать и находить соответствующее арифметическое действие. На этих занятиях не механически,а более или менее осознанно дети выполняют действия,аргументируют выбор арифметического действия. Задачи этого типа также следует сравнивать с задачами первого и второго типов. Вычислительная деятельность в дошкольном возрасте предполагает овладение арифметическими действиями сложения и вычитания,относящимися к операционной системе математики и подчиняющимися особым закономерностям операционных действий. Сложение и вычитание тесно связаны со счетом, пониманием состава числаиз единиц и двух меньших чисел,делением целого на части.Так, на рисунке28 представлены отношения междучисловыми данными, подводящие к выбору арифметического действия. Арифметические действия сложения и вычитания являются средством выполнения практических операций объединения и разъединения совокупностей и действий опосредованного сравнения.Арифметическая задача — основная форма выражения деятельности такого рода. Чтобы дети лучше запоминали числовые данные,используются карточки с цифрами, а впоследствии и знаки. Вначале числовые данные в задачах лучше ограничить первыми пятью числами натурального ряда. Дети в таких случаях,как правило,легко находят ответ. Основная цель этих 207 занятий— научить анализировать задачу. Дети учатся выделять структурные компоненты задачи, числовые данные, аргументировать арифметические действия. Особое внимание в этот период следует уделить обучению детей составлению и решению задач по иллюстрациям и числовым примерам. Составление и решение арифметических задач по числовому примеру требует сложной умственной деятельности,поскольку содержание задачи не может быть произвольным,а опирается на числовой пример как на схему. Например,воспитатель говорит: «Сейчас мы с вами будем составлять и решать задачи по картине».При этом привлекается внимание к картине, на которой изображена речка,на берегу играют пять ребят, а двое в лодках плывут к берегу.Предлагается рассмотреть картину и ответить на вопрос:«Что нарисовано на картине? О чем хотел рассказатьхудожник?Где играют дети? Сколько ребят на берегу?Что делают эти дети (показывает на детей в лодке)?Сколько их?Когда они выйдут на берег, их станет больше или меньше? Составьте задачу по этой картинке». Воспитатель вызывает двух-трех ребят и выслушивает составленные ими задачи.Потом выбирает наиболее удачнуюзадачу,и все вместе решают ее. «О чем идет речь в задаче? Сколько детей играли на берегу? Сколько детей приплыло в лодке?Что надо сделать,чтобы решить задачу? Как к числу пять можно прибавить число два?»5+1+1=7. Воспитатель следит за тем,чтобы правильно формулировалось арифметическое действие и объяснялся прием присчитывания по единице. Аналогично составляют и решают другие задачи. В конце занятия воспитатель,подводя итог,спрашивает,чем занимались на занятии,уточняет ответы:«Правильно,мы учились составлять и решать задачи,выбирать соответствующее действие, прибавлять и вычитать число два путем присчитывания и отсчитывания по единице». Примерно так же дети составляют и решают задачи по числовому примеру. Вначале обращают внимание на само действие.В соответствии с действием(сложение или вычитание)составляются условие и вопрос к задаче. Можно усложнить цель — не по каждому числовому примеру составляетсяновая задача, иногда по одному и тому же примеру составляются несколько задач разных типов.Это, естественно,значительно сложнее, зато наиболее эффективно для умственного развития ребенка. 208 Так,по числовому примеру 4+2 дети составляют и решают две задачи:первую — на отношение больше на несколькоединиц(на 2) и вторую— на нахождение суммы (скольковсего).При этом ребенок должен осознавать отношения изависимости между числовыми данными. На основе примера4—2 они должны составить три задачи: первого,второго и третьего типа. Сначала воспитатель помогает вопросами,предложениями:«Сейчас мы составим задачу, где будут слова— на два меньше,а потом по этому самому примеру составим задачу,где не будет таких слов, и нужно будет определить разницу в количестве(сколько осталось).— А потом воспитатель спрашивает:«А можно ли на основе этого примера составить новую, совсем другую задачу?»Если дети сами не могут сориентироваться,то воспитатель подсказывает им: «Составьте задачу, где вопрос начинался бы со слов на сколько больше(меньше)». Такие занятия помогают понять основное— арифметические задачи по своему содержанию могут быть разными, аматематическое выражение(решение) одинаковое.В этот период обучения большое значение имеет«развернутый»способ вычисления,активизирующий умственную деятельностьребенка.Накануне воспитатель повторяет количественныйсостав числа из единиц.Потом предлагает прибавлять число 2 не сразу, а присчитывать сначала 1, потом еще 1. Включениеразвернутого способа в вычислительную деятельность обеспечивает развитие логического,при этом способствуя усвоению сущности этой деятельности. После того как у детей сформируются представления и некоторые понятия об арифметической задаче, отношенияхмежду числовыми данными, между условием и вопросом задачи,можно переходить к следующему этапу в обучении— ознакомлению с преобразованием прямых задач в обратные. Это даст возможность еще глубже усвоить математическуюформулу задачи, специфику каждого типа задач. Воспитательобъясняет,что каждую простую арифметическую задачу можно преобразовать в новую, если искомое задачи взять за одноиз данных новой задачи, а одно из данных преобразованной задачи считать искомым в новой задаче. Такие задачи, где одно из данных первой задачи является искомым во второй, а искомое второй задачи входит в данные первой,называются взаимообратными задачами. Итак,из каждой прямой арифметической задачи путемпреобразования можно сделать две обратные задачи. 209 8 Заказ1392 Если дети при решении задач с первых шагов будут ориентироваться на существенные связи и отношения,то слова стало,осталось и другие не дезориентируют их. Независимоот этих слов они правильно выберут арифметическое действие.Более того,именно на этом этапе педагог должен обратить внимание на независимость выбора решения задачи от отдельных слов и выражений. Ознакомление с прямыми и обратными задачами повышает познавательную активность,развивает способность логически мыслить. При решении любых задач детидолжны исходить из вопроса задачи.Взрослый учит ребенка аргументировать свои действия,в данном случае аргументировать выбор арифметического действия. Ходмыслей при этом может идти по схеме:«Чтобы узнать..., нам необходимо..., потому что...» и т.д. В группе детей седьмого года жизни можно ознакомитьс новыми приемами вычислений— на основе счета группами.Дети, научившись считать парами,тройками, могут сразу прибавлять число 2, а потом и 3. Однако спешитьс этим не следует.Важно, чтобы у них сформировалисьпрочные,достаточно осознанные умения и навыки присчитывания и отсчитывания по единице. В современных исследованиях по методике математического развития есть некоторые рекомендации к формированию обобщенных способов решения арифметических задач. Один из таких способов— решение задач по схеме-формуле.Это положение обосновано и экспериментально проверено в исследованиях Н.И.Непомнящей,Л.П.Клюевой, Е .А.Тар-хановой,РЛ.Непомнящей.Предложенная авторами формула— это схематическое изображение отношения части и целого(рис. 29). Целое в данном случае— круг. Работой,предшествующей этому этапу,является практическое деление предмета(круга, квадрата,полоски бумаги)на части.То, что дети делают практически,воспитатель потом изображает в схеме-формуле.При этом он рассуждает так: «Если круг поделить пополам,то получатся две половины.Если эти половины сложить, то образуется снова целый 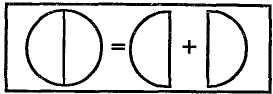 Рис.29 круг.Если от целого круга отнять одну часть, то получим другую часть этого круга. А теперь попробуем,прежде чемрешать некоторые задачи (подчеркивается слово некоторые),определить,на что ориентиру- 210 ет вопрос задачи:на нахождение части или целого.Неизвестное целое всегда находится сложением частей, а частьцелого— вычитанием». Например:«Для составления узора девочка взяла четыресиних и три красных кружочка. Из скольких кружочков девочка составила узор?» Дети рассуждают так: «По условиюзадачи рисунок составлен из синих и красных кружочков. Это части. Надо узнать, из скольких кружочков составлен узор.Это целое. Целое всегда находится сложением частей (4+3=7)». Для детей высокого уровня интеллектуального развития можно предлагать проблемные(косвенные)задачи. Ознакомление детей седьмого года жизни с задачами такого типа возможно и имеет большое значение для их умственногоразвития.На этой основе в дальнейшем будут формироватьсяумения осуществлять анализ более сложных арифметических задач, объяснять ход решения,выбор арифметическогодействия.Косвенные задачи отличаются тем, что в них оба числа характеризуют один и тот же объект, а вопрос направлен на определение количества другого объекта.Трудности в решении таких задач определяются самой структурой и содержанием задачи. Как правило, в этих задачах естьслова,которые дезорганизуют ребенка при выборе арифметического действия. Несмотря на то что в условии задачи есть слова больше,прилетели,старше и др., следует выполнять как бы обратное этому действие— вычитание.Для того чтобы ребенок правильно сориентировался,воспитатель учит его более тщательно анализировать задачу. Чтобы выбрать арифметическое действие, ребенок должен уметь рассуждать,логически мыслить. Пример косвенной задачи: «В корзине лежит пять грибочков, что на два грибочка больше, чем их лежит на столе. Сколько грибочков лежит на столе?» Часто дети, ориентируясь на несущественные признаки, аименно на отдельные слова (в данном случае словобольше),спешат выполнить действие сложения,допуская грубую математическую ошибку. Воспитатель подчеркивает особенности таких задач,предлагая вместе порассуждать так: в условии задачи оба числа характеризуют один объект— количество грибов в корзине:в ней пять грибочков и в ней же на два больше, чем на столе.Необходимо узнать, сколько грибочков на столе. Если в корзине на два больше, то на столе лежит на два грибочкаменьше.Чтобы узнать,сколько их на столе, следует от 5 вычесть2 (5-2=?). 211 При составлении задач воспитатель должен помнитьотом,что важно разнообразить формулировки в условии и вопросе задачи:насколько выше,тяжелее,дороже и т.д. Наряду с решениемарифметическихзадач предлагаются арифметические примеры, способствующие закреплению навыков вычислительной деятельности.При этом детей знакомят с некоторыми законами сложения. Известно,что всегда легче выполнить сложение, если второе слагаемое меньше первого.Однако не всегда именно такпредлагается в примере, может быть и наоборот— первое слагаемое меньше, а второе больше. Например,2+7=? В таком случае есть необходимость познакомить с перемести-тельным законом сложения:2+7=7+2. Сначала воспитатель показывает это на конкретных примерах, например на брусках.При этом он актуализирует знания о составе числа из двух меньших чисел.Дети хорошо усвоили, что число 9 можно образовать(составить) из двух меньших чисел: 2 и 7, или,что то же самое,7 и 2. На основе многочисленных примеров с наглядным материалом делают вывод-обобщение:действиесложения выполнять легче, если к большему числуприбавлять меньшее, а результат не изменится,если переставитьэти числа, поменять их местами. Итак,в методике математического развития дошкольников большое внимание уделяется проблеме обучения их вычислительной деятельности.Однако только в результате це-ленапраыюнной систематической работы у них формируются достаточно прочные и осознанные знания и навыки в вычислительной деятельности,а это важная предпосылка в овладении математикой в школе. Упражнения для самопроверки Детей в подготовительной группе зна комят с ... действиями— ... и вычитание, арифметическими Эта работа проводится... . На нескольких сложение поэтапно занятиях следует раскрыть... между ... ело- взаимосвязь жения и ....Ознакомление проводится на действиями основе... рисунков, по которым можно вычитания составить...на сложение и вычитание.Пос- рассматривания ле использования определенного количе- задачи ства...дети должны уметь сделать вывод: упражнений если от ...отнять второе слагаемое, томы суммы получим... слагаемое.Понимание ...между первое взаимосвязи сложением и ... используется в дальней- вытапииигм usем при проверке правильности ответа. 212 |
