|
|
щербакова учебник. Программа Учебники и учебные пособия для педагогических училищ и колледжей
i .
л» > ±ше ка вопросы,прохоянг в автобус, зани--„'ь с а разговаривают.Воспитатель предлагает про-BtN'iи/ "ш о ли пассажиры заняли места.
'!> *з 1 л'гг-п ,южет ехать автобус? (Считалкой выбирают водителя.)Водитель! Проверьте,хватит ли нам бензина? (Бакпустой,)Нам необходимо шесть литров бензина. А вот рядом бензоколонка.Водитель, проверьте по счетчику(отмеряется на счетчике переводом стрелки от одного деления к другому).А вы, заправщик,заправьте в бак шесть литровбензина.Дети, а вы смотрите,правильно ли наливают бензин,можно загибать на руках пальчики.Ну вот мы и можемехать.А в дороге, чтобы вам не было скучно, я буду тоже задавать вопросы».
Дети отвечают на вопросы.
Остановка.Выходят на полянку. «Полюбуйтесь лесом, прослушайте пение птиц.Пройдите по лесу, рассмотрите елочки,посчитайте шишки на них».Предлагается поиграть в игру«Найди свою елочку»(дети разбегаются по полянке, а по сигналу воспитателя бегут к своим елочкам — соотношение
164
своего номера с количеством шишек на елке).Игра повторяется дважды. Елочки меняются местами.
«Прислушайтесь,кто это перескакивает с ветки на ветку.Кто бы это мог быть? (Белки). А кто их видит? Вот они, шалуньи!А все ли они одинаковые?Давайте проверим(дети находят две одинаковые белочки). Дети,я нашла пакет.Что ж там написано? Может быть, это сорока потеряла. Это приглашение в Лесную школу.Но как же мы найдем дорогу к Лесной школе?» И вдруг видят большой камень, а на нем надпись(рассматривают ее). «Давайте прочтем. Налево пойдешь— в болото попадешь.Дети, где болото? (показывают).Направо пойдешь — к медведю попадешь.Назад пойдешь— дороги не найдешь, а вперед пойдешь— до Лесной школы дойдешь».
Задание для детей:«Повернитесь к самой высокой елочке лицом,сделайте три шага вперед,пять прыжков влево — вот и все дела».
«Дети!Вот и Лесная школа. Проходите,посмотрите,как тут зверята учатся».
Дети садятся за столы. На столе воспитателя цветок с разноцветными лепестками.На каждом лепестке написано задание.
I"1г ь CIvoтСьгьп ' !
] >■! т
р-*,о-
,■ - 1Г, , r , \ стрелка
по^ к. 1" * ч ' к. rtп каран-
датiv-iд.г• Т1"'
т к сг, 1 ! . •> гл м третий
< з " '* , • <• <, ■•■> 4Oi^ ля (за-
готсс * mi и1 t> г1■• j. '"••'ьзовать
игг
>гто (г-•■■ v1 " ''-нрави-
лесч.1 . о..l'k:\.:. (I ..ш-.г..*: _i..л.,,._. ,прислу
шайтесь,слышите?» (Дети находят под елочкой белку с кор
зинкой орехов).
За то, что дети старались,правильно отвечали, выполняли задания, бережно относились к лесу, к природе,лесные жители дарят им орехи.Все идут к автобусу через лес спесней.В автобусе воспитатель спрашивает у детей, что имбольше всего понравилось и запомнилось в путешествии.Таким образом, подводится итог занятия.
В старшей группе можно варьировать размещение пересчитываемых предметов. Дети должны научится считать предметы,размещенные по кругу, в виде числовой фигуры и в
165
бесструктурной,асимметричной группе. Важно при этом обратить их внимание на то, с какого предмета начинаютсчитать,чтобы не считать дважды один и тот же предмет и вместе с тем не пропустить ни одного. Поэтому целесообразно постепенно усложнять размещение предметов в пространстве.Ознакомив детей с разными способами счета, следует обратить их внимание на более удобный.Многократные упражнения подводят к выводу: начинать счет можно с любого числа,главное — не пропустить ни одного и не пересчитать дважды.
Как демонстрационный и раздаточный материалы достаточно часто используются числовые фигуры,а в последующем— цифры.
В старшей группе продолжается развитие счетной деятельности с участием разных анализаторов:счет звуков,движений,предметов на ощупь. Упражнения в счете предметов на ощупь значительно усложняются:для счета предлагаются более мелкие предметы, которые можно разместить на карточке в два ряда, в счете принимают участие все одновременно.Например, воспитатель проводит игру«Пошли,пошли, поехали».Предлагает детям стать в круг, руки спрятать за спину. Б руки каждого ребенка воспитатель вкладывает карточку, на которую нашиты пуговицы от1 до 5 штук. Они считают пуговицы,держа руки заспиной.На слова: «У кого 1 пуговица?У кого 2 пуговицы?»— дети показывают карточку с соответствующим количеством пуговиц.
Воспитатель объясняет правила игры:«Когда я скажу"пошли,пошли, поехали",— вы держите карточки перед собой, пуговицами вниз, чтобы их не было видно,и передаете один другому по кругу слева—направо или справа—налево.Когда я скажу"стой!", карточку,которая у вас будет в руках,спрячьте за спину и посчитайте на ощупь,сколько на ней пуговиц. Подглядывать нельзя!»
Педагог вместе с детьми становится в круг: «Слева направо пошли, пошли,поехали». Ребенок,который стоит от воспитателя слева, передает карточку ему,а сам получаеткарточку от соседа слева и т.д. Карточки постепенно передаются по кругу. На сигнал «стой!»дети прекращают передавать карточки, прячут руки с карточкой за спину, считаютпуговицы на ощупь. «У кого 2 пуговицы?У кого 3 пуговицы?»— спрашивает воспитатель.Дети показывают карточки. Числа можно называть как по порядку,так и в разбивку.Игру повторяют несколько раз.
166
Значительно шире для этой возрастной группы используется счет с участием слухового анализатора.Характер заданий постепенно усложняется.Если в средней группе дети считали только звуки,то в старшей можно соединять счет звуков и последующий отсчет предметов,сравнивать звуки и предметы по количеству.Кроме того,счет звуков можно объединять со счетом движений.
Установление количественных отношений между множествами,воспринятыми разными анализаторами,способствует обобщению счетной деятельности.
Упражнения для самопроверки
множествами представления
счете
числами
считать
количественного
порядкового
принцип
последующего
предыдущего
п-1
На шестом году жизни в процессе операций с ... у детей углубляются... о числе и ...,отношениях между ... , формируютсяпредставления об образовании чисел до десяти.
Детей учат...в пределах десяти, упражняют в распознавании...и... счета. Основное,чтобы усвоили...образования...за числом и числа п+1и любого... числа....
Ознакомление с количественным составом числа из единиц в пределах пяти.Шестилетние дети понимают не только то,что множество состоит из отдельных элементов, но и объясняют отношения числа к единице, т.е.подчеркивают количество единиц в числе.Эта работа проводится в пределах первых пяти чисел. При этом дети должны понимать, что все числа составляются из единиц, количество единиц в разных числах различно,оно соответствует различному количеству элементов множества(совокупности).
Для ознакомления с количественным составом чисел используется раздаточный и демонстрационный материал, в котором каждый элемент множества отличается от других элементов этого же множества по форме, цвету,размеру, назначению(рис. 22). Однако материал подбирают так, чтобы можно было делать обобщение:всего четыре кружочка, пять овощей. Дети уже знают на основе практических действий с множествами,что совокупности составляются из отдельных элементов, что количество элементов в совокуп-
167
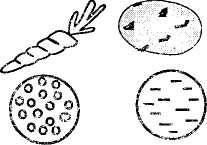
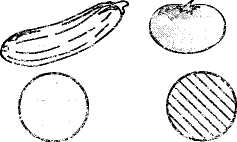
Рис, 22
кости соответствует числу. К этому понятию детей надо подводить постепенно, начиная с элементарного представления о множсстез и понимания их взаимоотношений к осмыслению числа как показателя мощности множества.
Следует напомнить еще раз, что в этой работе нельзя спешить. При изучении количественного состава числа первого десятка воспитатель подводит детей к пониманию единицы как отдельного элемента. В будущем, при подготовке к школе, эти знания станут основой формирования понятия о числе как показателе целой группы.
Сначала можно использовать однородный материал, каж-ттМй -.>^р,,-рт{Т г-ото^-л-о ся"ш-"рте>{ отчругих по размеру. Это
>■ < ' ol"'. 5 ■* создание ряда
1 * ,n. iv. i coit^^ -юла первого
< v r ! "■ vI-. j, л, а позже —
г i^ , ti' ^ .и просто счи-
^г , г ь ; - а ' iс" ль обращает
их внимание на количественный состав, предлагает называть все элементы множества. Например: «Сколько разных по размеру палочек нужно, чтобы составить это множество?» или «Сколько кружочков разного цвета нужно, чтобы составить это множество?» Возможны и другие варианты вопросов, заданий, а именно: как по названному числу создать множество из трех, пяти и больше элементов? Дети могут также рисовать разные предметы по заданным числам. Каждый раз после выполнения задания они рассказывают, как создали данную совокупность (множество).
Одно из занятий воспитатель может провести так.
Цель занятия. Ознакомить детей с количественным составом чисел 2,4 из единиц; научить составлять группы, которые вмещают определенное количество предметов одного вида, но отличаются качественными признаками (например, цветом).
Ход занятия. Воспитатель раскладывает на верхнюю полочку наборного полотна четыре квадрата синего цвета и
спрашивает: «Что это? Сколько квадратов?» Потом справа от синих квадратов размещает три квадрата разных цветов. И с-нова спрашивает детей: «Сколько квадратов в этой группе? Давайте все вместе посчитаем. Какого цвета квадраты? Сколько зеленых, красных, синих квадратов? Сколько всего квадратов? Правильно, в этой группе один квадрат зеленый, один синий и один красный, а всего три квадрата. Поровну ли квадратов в обеих группах? Как сделать, чтобы их было поровну?» Потом воспитатель вызывает одного ребенка и предлагает ему разместить квадраты разного цвета под синими, один под другим. Педагог спрашивает: «Сколько надо взять квадратов разного цвета, если я назову число четыре?»
Работас раздаточным материалом. У детей карточка с двумя незаполненными полосками, три кружочка зеленого цвета и три — разных цветов, коробка с цветными карандашами.
Воспитатель предлагает на верхнюю полоску положить три зеленых кружочка, а на нижнюю столько же кружочков разного цвета. «Сколько кружочков на верхней полоске? Сколько их на нижней? Сколько на ней кружочков каждого цвета?» Иа эти вопросы ребенок отвечает так: у меня на нижней полоске один красный, один желтый, один синий кружочек, всего три кружочка разного цвета. Воспитатель спрашивает: «Одинаково ли количество кружочков на верхней и нижней полосках? Почему? Сколько нужно взять предметов разных цветов, если я назову число три?»
Далее детям предлагают взять два (четыре) карандаша разного цвета. Уточняют, сколько карандашей каждого цвета взяли и сколько всего карандашей.
В конце занятия делается вывод: «Сегодня мы создавали группы из отдельных предметов и узнавали, сколько их нужно взять, чтобы получить множество из двух, трех или четырех предметов».
Понимание состава числа — очень важный момент подготовки детей к вычислительной деятельности. В подготовительной группе при обучении сложению и вычитанию чисел дети будут опираться на сочетательный закон сложения — прием присчитывания и отсчитывания по единице.
Упражнения для самопроверки
Дети шестого года жизни должны
знать ... состав ... из единиц в пределах количественный
пяти. числа
168
169
Сначала проводится большая ... рабо- практическая
та по сравнению соответствующих...пред- совокупностей
метов.Дети рассматривают группу пред
метов,или ее часть.Они должны пони
мать,что любое число составляется из
единиц.Общее ... единиц соответствует за- количество
данному.... или числу. множеству
Порядковое значение числа.Ознакомление с порядковымсчетом начинается в группе детей пятого года жизни. С шестилетками эта работа продолжается.
Умение считать, называя порядковые числительные,и понимать, чем они отличаются от количественных,имеет большое значение прежде всего для усвоения отношений между смежными числами натурального ряда, а в целом— успешного обучения в школе.
Как указывалось раньше, дети начинают использовать в своей речи порядковые числительные одновременно с количественными очень рано, уже в конце второго года жизни.
Перед воспитателем этой возрастной группы стоят задачи: научить детей порядковому счету в пределах десяти; умениюправильно отвечать на вопросы «Сколько?»,«Какой?», «Который».Именно в процессе обучения формируются представления о том, что числительное,которое было названо вовремя счета последним,дает ответ на вопрос «Сколько?»Часто следует знать не обо всех предметах группы, а о местеодного предмета в ряду других. В таких случаях вопрос ставится так: «На котором месте этот предмет?» или«Какой он попорядку?»В подобных ситуациях не пересчитывают все предметы,а считают только до того предмета,о котором хотелиузнать.При этом используются порядковые числительные.
В доступной форме необходимо объяснить детям, что результат количественного счета не зависит от порядка, в котором считают предметы. При этом важно лишь не пропуститьили не посчитатьдважды один и тот же предмет.И наоборот, для порядковых чисел направление счета имеет большое значение.В количественном и порядковом счете упражняются сначала с помощью предметов, а потом без них.
Ознакомление с порядковым значением числа происходит на основе сопоставления его с количественным значением.Детей подводят к пониманию того, что когда нужно узнать,сколько предметов всего, их считают так: один, два,три,четыре. В результате такого счета они могут ответить на
170
вопрос«Сколько?».Однако когда надо определить очередность,место предмета среди других,считают так:первый, второй,третий, четвертый.Это и будет ответом на вопрос «Который?»или «Какой по порядку?»
Порядковые числа люди используют для определениямаршрутов городского транспорта,номеров домов,мест в кинотеатре,автобусе и т.д.
Педагогическая практика свидетельствует о том, что детичасто путают вопросы«Какой?» и «Который?»Необходимообъяснить им, что первый вопрос требует выделения качественных признаков предмета (цвета,величины,назначения).Второй — определения места среди других. Чередованиевопросов«Сколько?»,«Который?»,«Какой» дает возможность раскрыть их значение.
Рассмотрим это на примере одного из занятий.
Цель занятия. Раскрыть значение порядковых числительных и сформировать навыки порядкового счета в пределах7. Показать, что для определения порядкового места предмета среди других существенное значение имеет направление счета.
Ход занятия. На столе у воспитателя7 одинаковыхкоробок.В одной из них спрятан шарик.«Сережа, посчитайкоробочки»,— говорит воспитатель.«Что сделал Сережа? О чем мы узнали?Правильно,Сережа посчитал коробочки, и теперь мы знаем,сколько их.Когда необходимо узнать, сколько предметов всего, их считают так, как это сделал Сережа:один, два, три и т.д. Благодаря этому получаютответ на вопрос «Сколько?»Всего семь коробок. Все коробки одинаковые,однако в одной из них спрятан шарик. Ее легконайти,если знать, на котором месте коробка с шариком.Когда требуется определить место предмета среди других,тоже считают,но числа называют иначе. Послушайте и посмотрите,как надо считать,когда хотят узнать, на котором месте предмет,который он по порядку».
Педагог считает слева направо: первая,вторая, третья...Которая по порядку последняя коробка? Детям предлагаетсяеще раз всем вместе(хором) посчитать коробки по порядку.
«Я вам открою секрет: шарик лежит в пятой коробке слева.Подойди, Галя,найди пятую коробку слева».Девочка находит пятую коробку и показывает шарик. Педагог следит за тем,чтобы ребенок использовал в своей речи порядковыечислительные.
«Дети,в каком направлении Галя считала коробки? — продолжает воспитатель.— А нашла бы она шарик, если бы
171
считала справа налево?Коля, проверь,если считать справа налево,то которая по порядку коробка с шариком?»Выясняется,что шарик в третьей коробке справа. «Валя,покажи пятую коробку справа. Видите,дети, как меняется место предмета среди других в зависимости от того, в каком направлении их считать.Поэтому, называя место предмета,всегда указывают направление счета: пятая слева, вторая справа.
Теперь обозначим место предмета, если считать слева направо.Закройте глаза,я положу шарик в другую коробку.Откройте глаза. Где шарик?Он в шестой коробке слева.Миша, найди шестую коробку».
Педагог еще два-три раза меняет место шарика.Дети, пользуясь порядковым счетом, находят его.
Работасраздаточнымматериалом.На столах у детей подносы с кружочками(квадратиками).Кружочки с одной стороны покрашены в синий цвет, а с другой в красный.Воспитатель предлагает детям положить семь кружков в ряд синей стороной вверх,найти четвертый кружочек(второй, шестой)слева и перевернуть его краснойстороной вверх.
«На котором месте у вас красные кружочки? Сколькоих?Которые по порядку синие кружочки?» При этом педагог каждый раз просит детей вслух посчитать кружочки, следит за тем, чтобы дети правильно называли порядковыечислительные.
После этого закрепляются навыки порядкового счета при увеличении количества предметов,которые нужнопосчитать,до десяти. Для этого широко используются разнообразный дидактический материал,дидактические игры типа:«Назови следующее число», «Сколько нас осталось?»,«Посчитай дальше от любого числа».
Некоторые дети, определяя место предмета,заменяют порядковые числительные количественными.Педагог следит,как они считают и указывает на ошибки. Особенно эффективны так называемые комбинированные упражнения,где порядковый счет соединяется со сравнением двух и более совокупностей предметов,группировкой геометрическихфигур,упорядочиванием предметов по величине и др.
В этой работе сначала используются однородные предметы,отличающиеся по цвету, размеру,а позднее —совокупности предметов разного вида,например силуэты животных,модели геометрических фигур и др.
Некоторое время (одно-два занятия) порядковый счет главенствует на занятии.После того как дети в основном
172
усвоят порядковый счет, на закрепление его можно отводитьуже только определенную часть занятия(начало или конец его).С целью прочного усвоения знаний эти задания повторяются на протяжении всего учебного года в старшей и закрепляются в подготовительной к школе группе.При этом следует помнить, что для повторения одной и той же темы интервалы между занятиями постепенно могут быть все более продолжительными.
Упражнения для самопроверки
Большое значение для усвоения от
ношений между ... числами... ряда имеет смежными
знание порядкового счета и понимание натурального
того,чем отличаются... числа от ... . порядковые
Целенаправленное обучение порядко- количественных
вому счету и ознакомление детей с поряд
ковыми... начинается в ... группе,уточня- числительными
ются эти знания в старшей. средней
В количественном и... счете дети упраж- порядковом
няются сначала с помощью..., а потом предметов
без них.
ги«л
юс,
ъ
Деление целого на части(
жества, а также отдельного (".v<
\яло ■
»хт
ратно сталкиваются в бы j, .о
приходилось делить между< >\» i
ты, печенье),покупать в м<< л ч i * , ,
хлеба,делить грядки на отдельные участки и т.д.
Деление целого предмета или множества на несколькоравных частей дает возможность познать ряд закономерностей в вещах и явлениях,способствует формированию логического мышления, развитию умения находить причинно-следственные связи, по результатам работы делать вывод об исходных данных и т.п.
С делением целого на. части дети знакомятся очень рано. На третьем-четвертом году жизни практически делили множество на части (отдельные элементы). Выполняли они и обратные действия — из отдельных элементов(частей) создавали целое множество.При этом ставилась задача определить количество элементов(фактически— частей) в данноммножестве,однако не рассматривались,а потому и не осознавались отношения части к целому.
Позднее,при ознакомлении с количественным составом чисел первого десятка,основное внимание уделялось имен-
173
но пониманию детьми отношения единицы (как части) к числу(как целому).
Однако педагогический опыт показывает,что без целенаправленного обучения делению на части не формируются четкие представления о целом и его частях, об отношениях части к целому,о связях между частями (равные и неравные) и т.п.
Процесс ознакомления детей с делением целого на частисостоит из таких компонентов:деление множества на подмножество,практическое деление предмета на части путем складывания,разрезания,на основе измерения и получениецелого из частей, т.е.установление отношений части и целого.Сначала воспитатель показывает детям, что множествамогут быть однородными и неоднородными,состоящими из двух-трех частей. Эти части можно объединять.Например, зайчиков и медведей дети воспринимают и считают как два самостоятельных множества (две совокупности,группы). «Сколько зайчиков? Сколько медведей? Чего больше? Чегоменьше?Как одним словом можно назвать и зайчиков, имедведей?Правильно, это игрушки». Итак,воспитатель подводит детей к тому,что количество отдельных небольшихмножеств можно объединять в одно большое множество. Этопоследнее множество называется целым, а первичные(небольшие)множества —частями этого целого. Целое всегда больше,чем любая его часть (даже самая большая).
Дети рассматривают букет из разных цветов и устанавливают,что букет — это целое, ромашки и васильки —его части.Ромашек в букете больше, чем васильков,однако их меньше,чем всего цветов в букете. Такие упражнения воспитатель организует на двух-трех занятиях. Постепенно дети делают вывод, что целое множество можно разделить на части,что часть (даже самая большая)меньше, чем целое, а целое больше, чем часть.
Для закрепления и уточнения этих понятий используются дидактические игры и упражнения типа «лото».Дети группируют,классифицируют предметы по определенным признакам,свойствам.
Особое значение имеют упражнения в практическом делении целого предмета на равные (а потом и неравные)части и на основе этого — осознание понятий «половина»,«одна вторая», «четверть»,«три четвертых»и т.д. Работа эта сложная,поэтому не следует форсировать отдельные ее моменты.Занятия планируются в определенной последовательности и представляют собой систему,где каждое звено (кон-
174
кретное занятие) тесно связано с предыдущим и последующим.Последовательность в обучении делению целого на части обоснована в работах Т.В.Тарунтаевой.
Первое занятие, посвященное ознакомлению с делением целого на части,следует рассматривать как вступительное.Основная цель этого занятия— создание определенной заинтересованности детей самим процессом деления,понимания ими практической необходимости этих действий.Для повышения заинтересованности и познавательной активности упражнениям часто придают игровой характер. Например,к кукле Наташе в гости пришлаее подруга, у них одно яблоко на двоих. Часть детей можетпредложить отдать яблоко подруге, однако будут и такие,кто предложит разделить яблоко пополам,поровну. Воспитатель делит яблоко пополам. Закрепляются слова-понятия:половина,две части, поровну.На этом же занятииможно предложить детям разлить поровну сок в две чашки.Следует подчеркнуть,что часть сока(половину) надовылить в чашку Наташе,остальную (тоже половину) — ее подруге. Воспитатель обращает их внимание на одинаковое количество сока в обеих чашках.
Детям предлагается самостоятельно поделить лист бумаги пополам,согнув и разрезав его. При этом воспитатель не спешит разрывать лист на части. Он сгибает его и уточняет, что образовались две половины,потом разгибает лист, чтобы все увидели,что из двух половинок можно составить снова целое.
Такие занятия можно проводить как комбинированные,т.е.обучение делению целого на части соединить с другими программными задачами(ознакомление с величиной,формой и др.). На втором и третьем занятиях знания и умениязакрепляются.Дети делят предмет (круг,полоску, ленту)на две равные части и из частей создают целое.Например,воспитатель берет лист бумага и обращается с вопросом:«Сколько у меня листов?»— «Один», — отвечают дети. Потом воспитатель сгибает лист бумаги пополам.«Сколько теперь листов?» — «Два»,— отвечают дети. «А если сложить так,как было, чтомы будем иметь?»— «Будем иметь один лист». В этих упражнениях дети учатся объединять отдельные части в целое, и наоборот— делить целое на части. Потом воспитатель показывает принцип деления целого предмета на четыре равныечасти.Как пример приведем одно из занятий.
Цель занятия. Научить делить целое на две, четыреравные части, сгибая предмет пополам(на две части)и еще
175
раз пополам (на четыре части);научить рассказывать о своих действиях и результате деления (сложив пополам, получимдве равные части,половина целого,одна из двух частей); сформировать представления о том, что половина— это одна издвух равных частей целого. Половинами называют обе равные части;показать отношения между целым и частью (целое больше,чем часть; часть меньше, чем целое).
Ход занятия, Воспитатель говорит: «У меня бумажная полоска, я складываю ее пополам,точно подравниваюконцы,заглаживаю линию сгиба.На сколько частей я поделила полоску? Правильно,я сложила полоску один раз пополам и поделила ее на две равные части. Сегодня мы с вами будем делить предметы на равные части.Равные ли эти части?»Педагог складывает полоску, убеждая детей в том,что части равные. «Получили две равные части. Вот одна половина полоски, а вот другая половина»,— показывает и объясняет воспитатель.«Что я сейчас показала? Сколько всего половинок?Что называется половинкой?»Педагог уточняетответы детей: «Половина— это одна из двух равных частей целого.Половинами называются обе равные части. Скольковсего таких частей в целой полоске?Как я получила две равные части? Что больше:целая полоска или одна из двух равных частей? Что меньше? А если я сложу полоску вот так (не пополам), на сколько частей я поделю ее?Можно ли эти части назвать половинами?Почему?»
Дети складывают круг пополам один раз, воспитательспрашивает:«Что получилось?»Детям предлагают рукой обвести каждую из половинок круга и задают вопрос: «Чтобольше(меньше) — целый круг или одна из двух равныхчастей(половина его)?»
Другому ребенку можно предложить сложить круг пополам,а потом еще раз пополам. Он складывает круг два разапополам,а педагог спрашивает детей: «Сколько раз был сложен круг пополам?Сколько получилось частей? Равные ли это часта?» ребенок обводит рукой каждую из четырех частей.
Воспитатель спрашивает:«Что больше(меньше) — однаиз четырех частей целого или целый круг?Сколько образовалось частей? А сколько теперь получилось,когда мы сложили круг дважды пополам?»
Во второй части занятия дети работают с раздаточнымматериалом.У каждого ребенка по два прямоугольника из бумаги.Предлагается сложить прямоугольник один раз пополам.Педагог напоминает,что складывать нужно так, чтобы стороны и углы совпадали.Задает вопросы:«Что мы сде-
176
лали?Что мы получили?Равные ли это части? Как называются обе равные части целого?Что больше(меньше) — половина целого или целый прямоугольник?»
Педагог предлагает второй прямоугольник дважды сложить пополам и спрашивает:«Что мы сделали?Что получили?»Дети обводят пальцем каждую из четырех частей.
В конце занятия воспитатель спрашивает:«Что вы научились делать? Если предмет сложить один раз пополам,то сколько частей будем иметь? Какие это части? Как они называются?Сколько раз надо сложить предмет пополам,чтобы получить четыре равные части?»
Дети должны понимать,как части относятся к целому. Для этого воспитатель раздает по два листа бумаги,одинаковые по размеру и форме. Один лист дети делят,второй остается целым. После того как они разделят лист на четыре части,показывают по просьбе воспитателя одну четвертую,две,три четвертых листа, а потом— целый лист.«Как можно сравнить целый лист бумаги с его частями,которые получили в результате деления?» —спрашивает воспитатель.Дети на целый лист накладывают часть и убеждаются,что целое больше,чем часть, а часть меньше целого.
На последующих занятиях знания уточняются и обобщаются.Ребята осознают,что единицы времени можно условно поделить на части: части суток, времена года, дни недели и др. Учатся делить на части не только разьединением,сгибанием,разрезанием,но и на основе измерения.
Величины можно разделить на части, измерив их, т.е. сравнитьс определенной величиной,которую принимают за единицу измерения.Ж.Пиаже утверждал,что измерение включает две логические операции: первая— это процесс деления, которая дает возможность ребенку понять,что целое состоит из определенного количества слеженных вместе частей;другая — это операция смещения или замещении,которая дает ему возможность присоединить одну часть к другой и так создавать систему единиц.
К измерению при делении целого на части, как правило, обращаются тогда, когда нельзя сгибать предмет. Например,воспитатель рисует на доске продолговатый невысокий прямоугольник и предлагает детям подумать,как можно разделить его на четыре равные части. (На столе воспитателя лежит шнур,по длине равный длинной стороне прямоугольника.)
С помощью наводящих вопросов: «Чем можно измеритьпрямоугольник?Как можно разделить шнур? Какую следует выбрать меру?» — дети должны прийти к решению: необхо-
177
димо шнуром измерить длиную сторону прямоугольника, убедившись, что она равна длине шнура, сложить шнур пополам и еще раз пополам. Сложенный шнур четыре раза отложить на стороне прямоугольника, сделать мелом отметки. Потом делают обобщение: «Мы разделили прямоугольник, изображенный на доске, на четыре равные части, каждая из этих частей называется одной четвертой».
Воспитатель постоянно побуждает к словесному описанию способа и результата деления. Дети устанавливают связь между действием и его результатом: разделили предмет пополам (дважды пополам) — получили две (четыре) равные части, объединили их вместе — получили целый предмет.
По просьбе воспитателя находят одну из двух частей (половинок), одну из четырех частей, две, три из четырех частей. Воспитателю следует помнить, что знания и умения детей делить предмет на части целесообразно использовать для расширения представлений о размерах геометрических фигур, о пространстве, времени. Например, когда делят квадрат, прямоугольник, ромб на равные части, получают при этом разные геометрические фигуры. Иногда детям дают конкретные задания: «Как следует сложить квадрат, чтобы получить два равных треугольника (прямоугольника)?» (рис. 23).

Рис. 23
Знание о делении целого на части и сложении целого из частей, полученные на занятиях по математике, закрепляются в изобразительной деятельности, конструировании и т.д. Эти знания и умения расширяются и уточняются в подготовительной к школе группе. Понимание детьми отношения части и целого, в дальнейшем можно использовать при обучении их решению арифметических задач.
Упражнения для самопроверки
необходимостью
целого части
делением
Одной из задач обучения детей в группе шестого года жизни является ознакомление их с возможностью и ... деления... на .... Процесс ознакомления детей с ... целого на части состоит из нескольких этапов:
подмножества
предмета
сгибания
измерения целого
отношений
деление множества на ... ;
практическое деление ... на части пу
тем ..., разрезания;
на основе ...и образования ...из час
тей, т.е. установления... части и целого.
|
|
|
 Скачать 2.02 Mb.
Скачать 2.02 Mb.