Навигация по странице:Р= 2М
|
курсовая работа. курсовая работа ДМ Сапронов. Разработка механического привода ленточного транспортера пз08
5.5 Цилиндрическая передача
В прямозубой передаче зубья входят в зацепление сразу по всей длине. Из-за неточности изготовления передачи и ее износа процесс выхода одной пары зубьев из зацепления и начало зацепления другой пары сопровождается ударами и шумом, сила которых возрастает с увеличением окружной скорости v колес. Прямозубые передачи применяют при невысоких и средних окружных скоростях.
Согласно основной теореме зацепления [см. формулу (1)] для понижающих передач
i=ω1/ω2=dд2/dд1=z2/z1 (26)
Для пары цилиндрических зубчатых колес рекомендуется i<=3…6; наибольшее значение i=12,5 (ГОСТ 2185
66).
Размеры зубчатого колеса выражают через модуль зацепления m и число зубьев z.
Диаметры делительной и начальной окружностей
dд=d=mz. (27)
Диаметр окружности выступов
De= dд+2h׳= dд+2m. (28)
Диаметр окружности впадин.
Di= dд+2h׳׳= dд+2,5m. (29)
Межосевое (межцентровое) расстояние передачи
A=(dд1 + dд2)/2= dд1·(1+i)/2=m z1(1+i)/2=m·zc/2, (30)
где zc = z1 + z2 — суммарное число зубьев.
Зная zc определяют число зубьев шестерни z1 = zc/(1+i). и колеса z2= zc- z1.
Силы взаимодействия между зубьями принято определять в полюсе зацепления р.
Распределенную по контактным линиям нагрузку в зацеплении заменяют равнодействующей Рn, которая направлена по линии давления (зацепления - нормали NN). Силами трения в зацеплении пренебрегают, так как они малы. Для расчета зубьев, валов и опор усилие Рn раскладывают на составляющие: окружное усилие
Р = Рn·cos α = 2·М1/ dд1 = М1·(1+ i)/A (31)
радиальное усилие
T=P·tg α (32)
где М1 — вращающий момент на шестерне.
На ведомом колесе направление усилия Р совпадает с направлением вращения, на ведущем и противоположно ему.
Основным критерием работоспособности открытых передач является прочность зубьев на изгиб. При выводе расчетной формулы принимают следующие допущения:
1. Вся нагрузка Рn зацепления передается одной парой зубьев.
2. Зуб рассматривают как консольную балку, нагруженную сосредоточенной силой Рn, приложенной к зубу в его вершине.
Эта сила, действующая под углом и к оси зуба, вызывает в его сечениях напряжения изгиба и сжатия. Силу Рn переносят по линии зацепления до оси зуба и полученную точку принимают за вершину параболы, которая определяет контур балки равного сопротивления изгибу. Точки F и Н касания ветвей параболы и профиля зуба определяют положение опасного сечения зуба на изгиб.
3. Сила трения в зацеплении и сжимающей действие силы Рn мало влияют на величину напряжения и поэтому не учитываются.
При этих допущениях напряжение изгиба в опасном сечении корня зуба
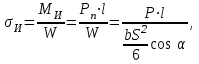
где W = bS2/6 — осевой момент сопротивления опасного сечения корня зуба.
Плечо изгиба l и ширину зуба в опасном сечении S выражают через модуль зацепления:
l = μm; S=νm,
где μ и ν — коэффициенты, учитывающие форму зуба.
Тогда
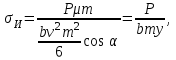
где. 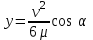 — коэффициент формы зуба. — коэффициент формы зуба.
Заменив Р= 2М1/dд1= 2М1/mz1, получим 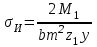 . .
Учитывая динамическое действие нагрузки и неравномерное распределение ее по длине зуба поправочным коэффициентом K, а износ зуба — поправочным коэффициентом γ, получим формулу для проверочного расчета открытых прямозубых передач:
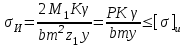 (33) (33)
где b=b2 — ширина обода колеса.
Выразив значение b2 через m, т. е. b2 = ψm·m, получим формулу для проектного расчета открытых прямозубых передач:
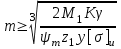 , (34) , (34)
где М1— вращающий момент на шестерне;
К — коэффициент нагрузки (см. ниже);
γ — коэффициент износа. В зависимости от допустимого износа зуба 10—30% соответственно принимают γ = 1,25 — 2;
ψm=b2/m — коэффициент ширины обода колеса по отношению к модулю. Для прямозубых передач общего назначения рекомендуется принимать ψm=10…20, соблюдая при этом условие b2<=dд1.
При выборе коэффициента ψm следует учитывать соображения, изложенные при расчете фрикционной передачи. Ширину обода шестерни b1 выполняют на 5…10 мм больше расчетной, учитывая возможное осевое смещение зубчатых колес из-за неточности сборки;
у — коэффициент формы зуба шестерни или колеса;
[σ]и — допустимое напряжение изгиба для материала шестерни или колеса.
Коэффициент формы зуба у. Коэффициент у — величина безразмерная, зависит от числа зубьев z, коэффициента смещения ξ, угла зацепления α, отношения высоты головки зуба h' к модулю зацепления m, т. е. h'/m=f0 (см. табл. 6.6 /1/).
Из-за меньшего числа зубьев зуб шестерни у основания более тонкий, чем у колеса; это отражено в меньшей величине коэффициента у (у1<у2). Для обеспечения примерно равной прочности зубьев шестерни и колеса шестерню делают из более прочного материала, чем колесо (см. табл. 6.4).
Зубья шестерни и колеса будут иметь равную прочность на изгиб при условии
у1[σ]и1=у2[σ]и2 (35)
В формулы (6.33) и (6.34) подставляют значения у и [σ]и того колеса, для которого меньше произведение у·[σ]и.
Коэффициент нагрузки К. При работе зубчатых передач вследствие возможных неточностей изготовления и сборки в зацеплении возникают дополнительные динамические нагрузки. Кроме того, деформация валов, корпусов и самих зубчатых колес приводят к неравномерному распределению нагрузки по длине зуба, вызывая ее концентрацию.
Влияние указанных явлений при расчете передач на прочность учитывается коэффициентом нагрузки К. Вводя этот коэффициент, повышают расчетную нагрузку передачи, что приводит к увеличению ее размеров.
При проектном расчете зубчатых передач коэффициентом К предварительно задаются:
К = 1,3 — при симметричном расположении колес относительно подшипников;
К= 1,4 — 1,6 — при несимметричном или консольном расположении колес.
При проверочном расчете зубчатых передач коэффициент нагрузки уточняют:
K׳=Kдин·Kкц (36)
где Кдин — динамический коэффициент, учитывающий дополнительные динамические нагрузки (табл. 6.7 /1/).
Ккц — коэффициент концентрации нагрузки, учитывающий неравномерное распределение нагрузки по длине зуба, вследствие деформации зубчатых колес, валов и подшипников, а также погрешностей при изготовлении и сборке передачи (см. табл. 6.8 /1/).
Для колес с твердостью зубьев
Kкц= (K׳кц+1)/2 (37)
где K׳кц — подставляют из табл. 6.8 /1/. Для тех же колес, но при нагрузке, близкой к постоянной, Kкц=1.
Проверку прочности зубьев на предотвращение пластической деформации или хрупкого разрушения при изгибе от действия кратковременных пиковых нагрузок ведут по [σ]и пред.
σи пик=σи М1 пик/М1 (38)
где σи пик — расчетное напряжение изгиба при перегрузках от М1 пик действующего на шестерню в период пуска, торможения, буксования и т. д.;
σи — расчетное напряжение изгиба по формуле (33) от номинального момента М, на шестерне.
|
|
|
 Скачать 0.95 Mb.
Скачать 0.95 Mb.