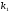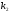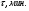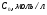Роберт Вильгельм Бунзен
 Скачать 2.24 Mb. Скачать 2.24 Mb.
|
|
ОСНОВЫ МОЛЕКУЛЯРНОЙ КИНЕТИКИ Для того чтобы произошла химическая реакция, сначала молекулы должны столкнуться. Один из результатов этого столкновения – химическое превращение, сопровождающееся разрывом «старых» и образованием «новых» связей. Теория, описывающая кинетику реакции, решает как задачу расчета чисел столкновений реагирующих молекул, так и задачу о собственно химическом превращении в комплексе столкнувшихся частиц. Заслуживает внимание две основные теории молекулярной кинетики: - теория столкновений; - теория переходного состояния; Описание кинетики реакции на основании свойств реагирующих частиц в этих теориях неодинаково. В частности в теории столкновений больше внимания уделяют расчету чисел столкновений молекул. И напротив, в теории переходного состояния подробнее исследуется сам акт химического взаимодействия в комплексе столкнувшихся частиц. ТЕОРИЯ АКТИВНЫХ СТОЛКНОВЕНИЙ Возьмем бимолекулярную газофазного реакцию: А+В→С+D Теория столкновений исходит из соображения, что бимолекулярная реакция может произойти только тогда, когда частицы реагентов А и В сталкиваются. Поэтому число элементарных актов реакции А + В → в единице объема пропорционально числу столкновений 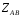 между частицами А и В в единицу времени. Из молекулярно-кинетической теории газов известно, что: между частицами А и В в единицу времени. Из молекулярно-кинетической теории газов известно, что: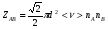 , где , гдеd- средний эффективный диаметр молекул; <  >- среднеарифметическое значение скорости молекул; >- среднеарифметическое значение скорости молекул;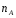 и и 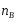 - число молекул А и В в единице объема. - число молекул А и В в единице объема. Чтобы при столкновении произошла реакция, необходимо, чтобы сталкивающиеся молекулы обладали некоторым запасом кинетической энергии 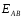 , необходимой для ослабления или разрыва связей в этих молекулах. Такие столкновения называются активными. , необходимой для ослабления или разрыва связей в этих молекулах. Такие столкновения называются активными.Если исходить из распределения Максвелла молекул по скоростям, доля активных столкновений в единицу времени от общего числа 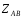 пропорциональна величине пропорциональна величине 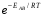 Отсюда следует, что число активных столкновений равно 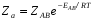 или или 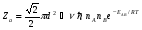 Значение Z 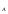 определяет скорость реакции, выраженную числом прореагировавших молекул А и В в единице объема за единицу времени. определяет скорость реакции, выраженную числом прореагировавших молекул А и В в единице объема за единицу времени.Выразив 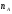 и и 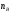 через молярные концентрации, а скорость в моль/см через молярные концентрации, а скорость в моль/см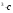 получим получим 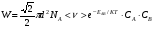 Сравнивая, это выражение для скорости со скоростью бимолекулярных реакций получим: 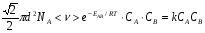 Отсюда находим, что k= 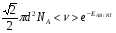 Если ввести обозначения для величин 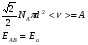 получим: 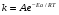 Множитель А в уравнении Аррениуса, согласно теории активных столкновений, равен числу столкновений в одном см 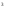 за 1с (выраженному в молях) при за 1с (выраженному в молях) при 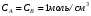 Проверка теории показала, что в отдельных реакциях вычисленные по опытным данным значения А хорошо согласуются с рассчитанными по уравнению: 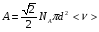 Но для некоторых реакций значения А, найденные опытным путем, на несколько порядков меньше рассчитанных. Имеются также реакции, для которых опытные значения А превышают теоретически рассчитанные. Для объяснения расхождений теории с опытными данными было предложено ввести поправочный множитель, учитывающий ориентацию молекул в пространстве в момент столкновения по отношению друг к другу: 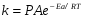 При благоприятной ориентации молекул Р=1, при неблагоприятной Р<1. Введение стерического множителя, качественно учитывающего геометрию столкновения молекул, не могло объяснить причину высоких значений А, т.е. Р не может быть больше единицы. ТЕОРИЯ ПЕРЕХОДНОГО СОСТОЯНИЯ Положения теории переходного состояния (ТПС) разработаны Г.Эйрингом и М.Поляни в 30- х годах 20- го столетия. Они получили выражение для расчета константы скорости и энергии активации простых реакций. Расчеты показали, что при сближении в процессе столкновения частиц А и В возрастает их потенциальная энергия Е 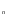 .На некотором расстоянии rа энергия Е .На некотором расстоянии rа энергия Е достигает максимума Еmax. достигает максимума Еmax.На этом расстоянии происходит реакция и образуются новые частицы С и D, которые затем удаляются и их потенциальная энергия падает (рис.10). 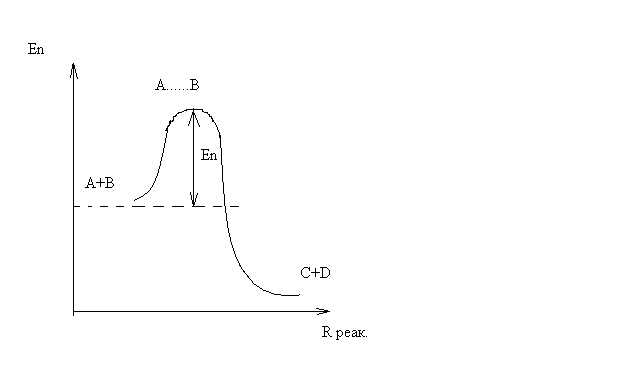  Рис.10 Рис.10Зависимость потенциальной энергии Еn от расстояния rреак, определяющего взаимное расположение атомов в реагирующих и образующихся частицах называется кривой потенциальной энергии. Расстояние 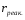 называется координатой реакции.Особенность кривых потенциальной энергии – это наличие максимума. Высота этого максимума равна энергии активации называется координатой реакции.Особенность кривых потенциальной энергии – это наличие максимума. Высота этого максимума равна энергии активации 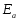 .Исходя из формы кривой потенциальной энергии, величину .Исходя из формы кривой потенциальной энергии, величину 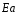 называют часто энергетическим или активационным барьером реакции. называют часто энергетическим или активационным барьером реакции.На вершине активационного барьера реагирующие частицы А и В образуют активированный комплекс (А…В), который существует непродолжительное время и быстро распадается, образуя продукты С и D: 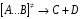 Активированный комплекс находится в равновесии с реагирующими частицами: 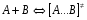 Константа активированного равновесия равна: 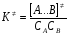 Отсюда следует, что концентрация 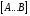 связана с концентрацией реагентов специального образования следующим образом: связана с концентрацией реагентов специального образования следующим образом: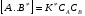 Скорость реакции пропорциональна концентрации этих комплексов, т.к. продукты реакции С и D образуются из этих комплексов: W= 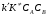 k´-коэффициент пропорциональности,  равный RT/ (N равный RT/ (N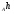 ),где ),где
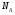 - число Авогадро; - число Авогадро;h- постоянная Планка; Сравнивая полученное выражение с законом действующих масс для скорости реакции W=kCa∙CB, получим выражение для константы скорости. 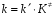 Чтобы получить зависимость теоретической константы скорости от температуры, следует использовать уравнение изотермы реакции Вант – Гоффа 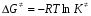 где где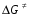 энергия Гиббса активации; энергия Гиббса активации;В соответствии с определением 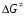 равна: равна: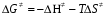 , где , где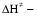 энтальпия активации; энтальпия активации;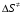 - энтропия активации; - энтропия активации;Равенство левых частей позволяет приравнять правые 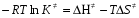 или 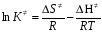 или 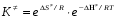 Подставим полученные значения К 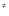 в выражение для константы скорости: в выражение для константы скорости: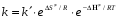 Сравнение последнего выражения с уравнением Аррениуса показывает, что предэкспонента равна: 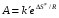 , ,а энергия активации: Еа = 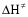 Таким образом, ТПС позволяет связать кинетику химических реакций с термодинамическими характеристиками процесса активации 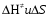 . .Из соотношения 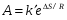 следует, что предэкспонента в уравнении Аррениуса определяется изменением энтропии в процессе образования активированного комплекса. Чем больше значение следует, что предэкспонента в уравнении Аррениуса определяется изменением энтропии в процессе образования активированного комплекса. Чем больше значение 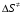 , тем больше А, тем быстрее протекает реакция. , тем больше А, тем быстрее протекает реакция.Изменение энергии взаимодействия между атомами, из которых состоят эти частицы, определяются энтальпией активации 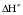 Возрастание этой величины сопровождается таким же возрастанием энергии активации Еа и уменьшением скорости реакции и наоборот. ЗАДАЧИ И ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ. Задача 1. В таблице для реакций N2O4→N2O3+1∕2O2 приведены значения констант скоростей при двух температурах. Необходимо вычислить: а) энергию активации; б) константу скорости при Т3; в) температурный коэффициент скорости; г) количество вещества, израсходованное за время τ Порядок реакции считать по молекулярности. Таблица
Решение. а) для нахождения энергии активации воспользуемся интегральной формой уравнения Аррениуса: 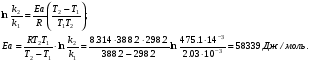 б) для нахождения к3 при Т3 воспользуемся той же формулой уравнения Аррениуса: 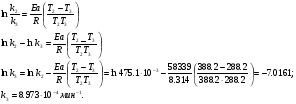 в) для определения температурного коэффициента скорости воспользуемся математическим выражением правило Вант – Гоффа: 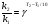 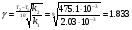 г) порядок реакции первый, поэтому воспользуемся кинетическим уравнением для реакций названного порядка: 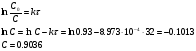 Задание 1. В таблице приведены значения констант скоростей при двух температурах. Вычислите: а) энергию активации; б) константу скорости при Т 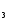 в) температурный коэффициент скорости; г) количество вещества, израсходованное за время τ. Порядок реакции считать по молекулярности. Начальные концентрации реагирующих веществ (с 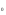 ) – одинаковы. ) – одинаковы.Таблица
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ Работа №1. Исследование скорости разложения тиосульфата натрия. Цель: изучить зависимость скорости реакции разложения тиосульфата натрия от концентрации, температуры и концентрации катализатора. Тиосульфат натрия разлагается в растворе серной кислоты по уравнению реакции: Na2S2O3 + H2SO4 → Na2SO4 + SO2 + S + H2O Реакция состоит из следующих стадий: 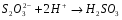 (очень быстро) (очень быстро)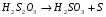 (медленно) (медленно)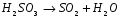 (быстро) (быстро)Скорость суммарного процесса определяется второй (медленной) стадией. Опыт № 1.Зависимость от концентрации. В пять пробирок наливают из бюреток 0.1М Na2SO3 и воду в количествах, указанных в таблице. В другие пять пробирок наливают из бюретки по 5 мл 1М H2SO4 (первый раствор приливают ко второму) и отсчитывают время до начала помутнения содержимого каждой пробирки. Результаты записывают в таблицу по форме:
В этом и следующих опытах измеряется не скорость реакции, а промежуток времени между началом реакции и ее видимым результатом, однако этот промежуток времени обычно пропорционален скорости реакции, поэтому величину назовем условной скоростью реакции W (усл.). Строят график зависимости скорости разложения тиосульфата от концентрации. Какой вывод можно сделать о порядке исследуемой реакции на основании полученной зависимости? | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||