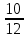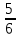Сборник суммативного оценивания по математике 6 класс. Сборник работ для суммативного оценивания по математике 6 класс
 Скачать 3.33 Mb. Скачать 3.33 Mb.
|
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 3 ЧЕТВЕРТЬПродолжительность – 40 минут Количество баллов – 20 Типы заданий: МВО – вопросы с множественным выбором ответов; КО – вопросы, требующие краткого ответа; РО – вопросы, требующие развернутого ответа. СТРУКТУРА СУММАТИВНОЙ РАБОТЫ Суммативная работа представлена в четырех вариантах. Каждый варинат состоит из 7 заданий, включающих вопросы с множественным выбором ответов, с кратким и развернутым ответом. В вопросах с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов. В вопросах, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения. В вопросах, требующих развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание может содержать несколько структурных частей/вопросов ХАРАКТЕРИСТИКА ЗАДАНИЙ СУММАТИВНОГО ОЦЕНИВАНИЯ
1 ВАРИАНТ
1. Какие из предложенных уравнений являются равносильными? А. -2х=-20 Б. (х – 4)(х + 4)=0 В. 3(х+8)=12 Г. х – 4=6 A) А, В и Г B) А и В C) Б и В D) А и Г 2. Из данных изображений выберите те, которые имеют ось симметрии:
3. Изобразите вектор 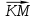 . Запишите начало и конец вектора. . Запишите начало и конец вектора.4. Катер за 2 часа по озеру и за 3 часа против течения реки проплывает такое же расстояние, что за 3,4 ч по течению реки. Найдите собственную скорость катера, если скорость течения реки равна 3 км/ч. 5. Решите уравнение: 4|х|+5|х|-3=2|х|+11 6. Приведите неравенство к виду kx ≥ b или kx≤ b: 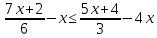 7. Отметьте на координатной плоскости точки М (-7;-3), N (4;5), K (-6;6) и P (7;-3). Проведите прямые MN и KP. Найдите координаты точки пересечения прямых MN и KP. Найдите координаты точки пересечения прямой MN с осью абсцисс. Найдите координаты точки пересечения прямой KP с осью ординат. СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
2 ВАРИАНТ
1. Какие из предложенных уравнений являются равносильными? А. 5х=-20 Б. (х – 3)(х + 8)=0 В. х – 4= –8 Г. 3(х+8)=1 A) А, В и Г B) А и В C) Б и В D) А и Г 2. Из данных изображений выберите те, которые имеют ось симметрии:
3. Изобразите вектор  . Запишите начало и конец вектора. . Запишите начало и конец вектора.4. Плот за 2 часа по озеру и за 3 часа против течения реки проплывает такое же расстояние, что за 2,5 ч по течению реки. Найдите собственную скорость плота, если скорость течения реки равна 0,6 км/ч. 5. Решите уравнение: 7|х|-2|х|+6=3|х|+12 6. Приведите неравенство к виду kx ≥ b или kx≤ b: 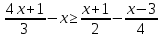 7. Отметьте на координатной плоскости точки М (-4;-4), N (-8;2), K (3;2) и P (-1;-5). Проведите прямые MN и KP. Найдите координаты точки пересечения прямых MN и KP. Найдите координаты точки пересечения прямой MN с осью абсцисс. Найдите координаты точки пересечения прямой KP с осью ординат. СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
3 ВАРИАНТ
1. Какие из предложенных уравнений являются равносильными? А. (х – 3)(х + 8)=0 Б. -3х=-9 В. х +5= 8 Г. 20(х+8)=1 A) А, В и Г B) А и В C) Б и В D) А и Г 2. Из данных изображений выберите те, которые имеют ось симметрии:
3. Изобразите вектор  . Запишите начало и конец вектора. . Запишите начало и конец вектора.4. Лодка за 1 час по озеру и за 4 часа против течения реки проплывает такое же расстояние, что за 2,6 ч по течению реки. Найдите собственную скорость лодки, если скорость течения реки равна 1,5 км/ч. 5. Решите уравнение: |2у+5|-8=5 6. Приведите неравенство к виду kx > b или kx< b: 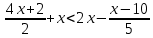 7. Отметьте на координатной плоскости точки М (-9;-1), N (4;6), K (1;7) и P (-7;-7). Проведите прямые MN и KP. Найдите координаты точки пересечения прямых MN и KP. Найдите координаты точки пересечения прямой MN с осью абсцисс. Найдите координаты точки пересечения прямой KP с осью ординат. СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
4 ВАРИАНТ
1. Какие из предложенных уравнений являются равносильными? А. х -5= -8 Б. -7х=21 В. (х – 8)(х +9)=0 Г. 100(х+8)=1 A) А, В и Г B) А и Г C) Б и В D) А и Б 2. Из данных изображений выберите те, которые имеют ось симметрии:
3. Изобразите вектор 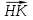 . Запишите начало и конец вектора. . Запишите начало и конец вектора.4. Прогулочный пароход за 0,4 часа по озеру и за 2 часа против течения реки проплывает такое же расстояние, что за 1,2 ч по течению реки. Найдите собственную скорость парохода, если скорость течения реки равна 3 км/ч. 5. Решите уравнение: 2|у+5|-8=4 6. Приведите неравенство к виду kx > b или kx< b: 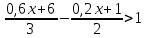 7. Отметьте на координатной плоскости точки М (-2;-4), N (4;2), K (-1;5) и P (-9;-5). Проведите прямые MN и KP. Найдите координаты точки пересечения прямых MN и KP. Найдите координаты точки пересечения прямой MN с осью абсцисс. Найдите координаты точки пересечения прямой KP с осью ординат. СХЕМА ВЫСТАВЛЕНИЯ БАЛЛОВ
СПЕЦИФИКАЦИЯ СУММАТИВНОГО ОЦЕНИВАНИЯ ЗА 4 ЧЕТВЕРТЬ Продолжительность – 40 минут Количество баллов – 20 Типы заданий МВО – вопросы с множественным выбором ответов КО – вопросы, требующие краткого ответа РО – вопросы, требующие развернутого ответа СТРУКТУРА СУММАТИВНОЙ РАБОТЫ Данный вариант состоит из 8 заданий, включающие вопросы с множественным выбором ответов, требующие краткого и развернутого ответов. В заданиях с множественным выбором ответов обучающийся выбирает правильный ответ из предложенных вариантов ответов. В заданиях, требующих краткого ответа, обучающийся записывает ответ в виде численного значения, слова или короткого предложения. В заданиях, требующие развернутого ответа, обучающийся должен показать всю последовательность действий в решении заданий для получения максимального балла. Оценивается способность обучающегося выбирать и применять математические приемы в ряде математических контекстов. Задание, содержит несколько структурных вопросов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

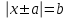 , где a и b – рациональные числа
, где a и b – рациональные числа


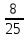 км/ч
км/ч


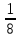 км/ч
км/ч