Метод виклад з мат-ки 2. Спеціальна методика викладання математики зміст методика розв'язування арифметичних задач
 Скачать 7.16 Mb.
|
|
Одним з основних завдань, які стоять перед вчителем у 3-му класі є формування в школярів вміння виконувати обчислювальні операції з невідомими компонентами. Цьому розділу програми присвячується достатня кількість часу. У 1 -му та 2-му класах учні також проводили обчислення даних прикладів, але при цьому вони не використовували закономірності знаходження невідомого складника: обчислення виконувалось в межах 10 і 20, застосовуючи прийом підбору, наприклад: + 3 = 10, 4 + 3 = 7 – неправильно, 5 + 3 = 8 – неправильно, 6 + 3 = 9 – неправильно, 7 + 3 = 10 – правильно. Починаючи з 3-го класу, вчитель знайомить школярів з правилом знаходження невідомого компонента. Перед початком пояснення цього матеріалу вчитель може створити проблемну ситуацію, розв'язання якої вимагає знання певного алгоритму: закриває один з компонентів приклада аркушем паперу, дає для розв'язання задачу тощо. Організовуючи таку роботу, він підводить школярів до розуміння того, що невідомий компонент можна знайти, якщо знати правило його пошуку. Для цього він дає означення: для знаходження невідомого доданка потрібно від суми відняти відомий доданок. Після цього розв'язується ряд прикладів, які підтверджують його правильність: + 12 = 20, 20 – 12 = 8, отже, = 8; + 18 = 30, 30 – 18 = 12, отже, = 12; + 21 = 34, 34 – 21 = 13, отже, = 13; + 26 = 42, 42 – 26 = 16, отже, = 16; 28 + = 37, 37 – 28 = 9, отже, = 9. Приклади даються з наростанням ступеня складності: спочатку простіші, які не вимагають переходу через розряд, а потім складніші, для обчислення яких потрібно виконати прийом переходу через розряд. Після усвідомлення алгоритму знаходження невідомого доданка вчитель переходить до пояснення обчислення невідомого зменшуваного або від'ємника. Дається визначення: для знаходження невідомого зменшуваного потрібно до різниці додати відомий від'ємник.Наводяться приклади: – 10 = 14, 14 + 10 = 24, отже, = 24; – 26 = 34, 34 + 26 = 60, отже, = 60; – 18 = 18, 18 + 18 = 36, отже, = 36; – 23 = 29, 29 + 23 = 52, отже, = 52. Провівши такі обчислення, вчитель організовує порівняння прикладів на знаходження невідомого доданка і невідомого зменшуваного: х + 14 = 27, 27 – 14 = 13, отже, х = 13 х – 12 = 26, 26 + 12 = 38, отже, х = 38. Це дозволяє зробити узагальнення: для того, щоб знайти невідомий доданок, потрібно виконати обернену дію, тобто віднімання; для того, щоб знайти невідоме зменшуване, потрібно виконати обернену дію, тобто додавання. Провівши обчислення достатньої кількості прикладів на знаходження невідомого доданка і зменшуваного, вчитель пояснює знаходження невідомого від'ємника. Запропонувавши для обчислення такий приклад: 24 – = 11. Більшість розумово відсталих дітей виконають його аналогічно знаходженню невідомого зменшуваного: 11+ 24 = 35, отже, = 35. Лише після того, як виконають його перевірку вони, пересвідчаться у неправильності даного обчислення. Тоді педагог формулює правило: для знаходження невідомого від'ємника потрібно від зменшуваного відняти різницю. 24 – = 11, 24 – 11 = 13, отже, = 13; 36 – = 22, 36 – 22 = 14, отже, = 14; 57 – = 19, 57 – 19 = 38, отже, = 38; 64 – = 28, 64 – 28 = 36, отже, =36; 85 – = 48, 85 – 48 = 37, отже, =37.   Провівши обчислення достатньої кількості прикладів на знаходження невідомого компонента, вчитель переходить до пояснення, що невідомий компонент, який використовувався у наших прикладах у вигляді пустої клітинки () може замінюватись літерою, наприклад "X", "А", "С" тощо, при цьому заміна пустої клітинки літерою не впливає на алгоритми його обчислення, наприклад:Х + 20 = 38, 38 – 20 = 18, отже, Х= 18; Х – 24 = 35, 35 + 24 = 59, отже, X = 59; 48 – X = 22, 48 – 22 = 26, отже, X = 26. Учням допоміжної школи притаманні труднощі утворення системи знань і вироблення узагальнених навичок. Тому вчитель проводить роботу по формуванню у школярів знань не з обчислення окремого типу прикладів, а над взаємодією даних знань з раніше вивченими. Наприклад, пояснивши школярам, як потрібно проводити обчислення прикладу типу 85 - 26 = вчитель на наступних заняттях пропонує виділити цей новий тип прикладів з ряду інших випадків (85 – 20 =, 80 – 6 =) для того, щоб підкреслити подібність і відмінність нового прикладу з уже знайомими. Вчитель не лише аналізує приклади, які пропонує школярам, але й дає їм можливість скласти подібні вже обчислені або робота над якими розглядалась в класі. Причому він може на дошці дати зразок, а потім запропонувати їм виділити даний тип прикладів серед інших і провести обчислення, використовуючи зразок. Урок вивчення арифметичних дій планується таким чином, щоб повторювався матеріал нумерації, матеріал попередніх уроків зіставлявся з новими знаннями, вивчались прийоми розв'язання задач, відбувалась підготовка до вивчення наступного матеріалу. 6. Методика вивчення множення і ділення 6.1. Формування в учнів поняття про множення і ділення При вивченні чисел в межах 100 учні знайомляться з двома видами множення і ділення: табличним і позатабличним. Табличне множення-це множення одноцифрового числа на одноцифрове. Табличне ділення — це ділення одноцифрового або двоцифрового числа на одноцифрове при одноцифровій частці.Вони і складають таблицю множення і ділення в межах 100. До позатабличного множення відносяться випадки множення двоцифрового числа на одноцифрове і навпаки, коли добуток цих чисел не перевищує 100. Позатабличним діленням називають ділення двоцифрового числа на одноцифрове, коли в частці отримуємо двоцифрове число і ділення двоцифрового числа на двоцифрове, коли в частці отримуємо одноцифрове число. Знання учнями допоміжної школи таблиці множення одно-цифрових чисел є запорукою вивчення математики взагалі. Без твердих знань цього матеріалу неможливо оволодіти обчислювальними навичками на всіх наступних роках навчання. Вивчення множення і ділення проводиться паралельно (крім випадків множення і ділення в межах 20): за таблицею множення одного числа розглядається відповідний випадок ділення. Такий порядок оволодіння даною темою, з одного боку, сприяє кращому запам'ятовуванню учнями результатів таблиці множення, з іншого – полегшує вивчення ділення. Він також допоможе їм краще зрозуміти зв'язок між цими діями, усвідомити, що множення – це додавання однакових доданків. Таблицю множення можна вивчати двома способами: за постійним множеним або за постійним множником. У допоміжній школі учні знайомляться і з двома видами ділення: діленням на рівні частини і діленням за змістом. При вивченні ділення необхідно враховувати наступні його особливості: і) ділення на рівні частини більш знайоме учням з їхнього досвіду; ділення за змістом їм не знайоме; 2) ділення на рівні частини більше зрозуміле учням; суть ділення за змістом складніше сприймається дітьми;   3) запис ділення на рівні частини простий і зрозумілий дітям; запис ділення за змістом важкий, складний для них.При вивченні табличного множення учнів спочатку знайомлять з випадками, коли постійним є множене, а при вивченні ділення – ділення на рівні частини. З діями другого ступеня вони знайомляться у 3-му класі. У 2-му класі при вивченні додавання і віднімання діти виконували різні вправи у рахунку рівними числовими групами по 2, 3, 4, 5 в межах 20. У 3-му класі вони, перед ознайомленням з діями ділення і множення, виконують рахунок на прилічування і відлічування рівними числовими групами в такому порядку:
У допоміжній школі зміст кожної арифметичної дії другого ступеня розкривається на конкретному матеріалі. Наочними посібниками і дидактичним матеріалом на цьому етапі навчання можуть служити іграшки, природний матеріал, кружечки, ґудзики, каштани, трафарети, малюнки тощо. Важливим є поєднання їх парами так, як вони зустрічаються в оточуючому середовищі. Вивчення кожного випадку табличного множення супроводжується відповідними вправами у груповому рахунку. Таким чином, основним обчислювальним прийомом множення є прийом набору рівних доданків. Це дає можливість дати учням перші уявлення про множення, з’ясувати його конкретний зміст. У практиці роботи допоміжної школи, в рекомендаціях методичного характеру набула поширення наступна система вивчення дій множення і ділення: 1) знайомство з множенням як додаванням однакових доданків; 2) знайомство з діленням на рівні частини; 3) розгляд випадків і складання таблиці множення і ділення в межах 20; 4) вивчення множення і ділення в межах 100 і складання таблиць множення і ділення; 5) практичне знайомство з переставним законом множення; 6) ділення із остачею; 7) ділення за змістом; 8) співставлення двох видів ділення в практичній діяльності; 9) множення 1 на число, на 1, ділення на 1; 10) 0 як компонент множення і 0 як ділене. Смисл дії множення натуральних чисел найкраще визначити, виходячи з додавання кількох однакових чисел. Помножити число а на число b означає знайти суму b доданків, кожен з яких дорівнює а. Ознайомлення з множенням краще починати з того випадку, коли множене дорівнює 2. Учням можна запропонувати задачу, для розв'язування якої потрібно знайти суму однакових доданків, а зміст її показати наочно. Наприклад: "4 хлопчики взяли по 2 яблука кожен. Скільки всього яблук взяли хлопці?" Для розв'язання задачі вчитель ставить перед учнями ряд запитань: "Що відомо в задачі? Що потрібно взнати?" При цьому один школяр робить ілюстрований запис на дошці, а діти виконують аналогічні малюнки у себе в зошиті. 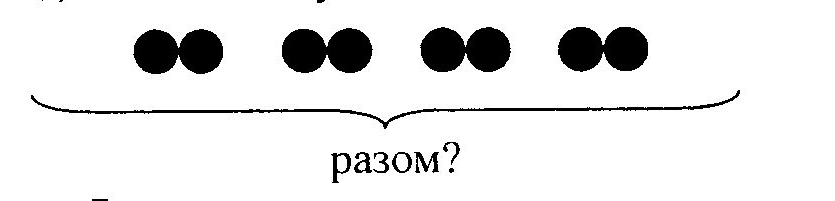 Вчитель запитує:
На дошці уявляється запис: 2 + 2 + 2 + 2 = 8 Відповідь: 8 яблук взяли діти. Таким чином, вчитель підводить дітей до висновку, що в цьому виразі всі доданки однакові. Оскільки до цього часу діти вивчали дві дії – додавання і віднімання, то тепер вони повинні познайомитись з дією множення, вміти її записувати, застосовувати і навчитись читати відповідні приклади. Вчитель повідомляє, що виконаний запис можна прочитати і по-іншому: "По 2 взяли 4 рази, отримали 8". Необхідно показати доцільність заміни додавання множенням, познайомити зі знаком множення (х, ∙ ) і з записом дії в рядок. Знання цієї дії закріплюються відповідними вправами. Як наочні посібники, використовуються предметні множини і картинки з зображенням предметів, об'єднаних у рівні групи. На   приклад: "Перерахуйте рукавиці, зв'язані парами". Діти рахують по 2 : 2, 4, 6, 8, 10. Вчитель запитує, скільки рукавиць зв'язані разом. Запишемо так, як рахували: 2 + 2 + 2 + 2 + 2 = 10. Скільки пар рукавиць? (П'ять.) Скільки усього рукавиць? (Десять). У цьому прикладі додавання можна замінити іншою дією – множенням і записати приклад коротше. Сказати можна так: "По 2 узяти 5 разів, вийде 10", а записати так: "2x5 = 10".Так само ведеться рахунок парами, наприклад, вишень, намальованих парами на картках; результат рахунка записується спочатку додаванням, а потім множенням: 2 + 2 + 2 + 2 = 8, 2 x 4 = 8 Вчитель запитує: "Яке число записується першим при множенні? (Доданок). Яке число записується другим? (Число 4). Що воно позначає?" (Число доданків). Формуються навички заміни додавання множенням. Корисні завдання з дидактичним матеріалом: "Узяти по 2 кубики 3 рази. Записати цю дію додаванням, замінити додавання множенням". (2 + 2 + 2 = 6, 2 x 3 = 6.) Для кращого усвідомлення матеріалу доцільно запропонувати дітям таблицю з назвами елементів дій (при цьому потрібно зазначити, що ці назви не потрібно ще вивчати напам'ять). Таблиця 6.1. Після цього можна запропонувати учням ще одне визначення: помножити одне число на друге - значить взяти перше число доданком стільки разів, скільки одиниць у другому числі При цьому те число, яке повторюється як доданок називається множеним; число, яке показує, скільки разів береться такий доданок - множником; число, одержане в результаті множення - добутком. Множене і множник ще деколи називаються співмножниками. Після цього можна перейти до складання таблиці множення на 2. Вона, як повідомлялось вище, складається по постійному множеному. Наведемо послідовність знайомства з табличним множенням числа 2:
3) заміна додавання множенням і читання таблиці множення. На початку вивчення цієї теми розбираються приклади: 2 + 2 = 4 2 + 2 + 2 = 6 2 + 2 + 2 + 2 = 8 Тут число 2 повторюється кілька разів. У першому рядку число 2 повторюється 2 рази, у другому – 3, у третьому – 4. Раціональніше не записувати кожен раз суму, яка складається з двох, трьох, чотирьох двійок, а вказати, скільки разів потрібно взяти по 2, тобто замінити додавання однакових доданків множенням. З метою засвоєння і закріплення знань проводяться вправи на заміну дії додавання множенням і навпаки: 2 + 2 + 2 = 2 x 3; 2 x 5 = 2 + 2 + 2 + 2 + 2. Учні повинні вміти проілюструвати приклад на множення рисунком, складати за малюнками приклади на додавання і множення. Потім таку ж роботу виконати самостійно на індивідуальних картках. Після того, як діти вивчили всі випадки множення на 2, вони складають таблицю множення. Не дивлячись на те, що вона є в підручнику і в кінці кожного зошита з математики, учні повинні записати її в зошитах. На наступному етапі школярі тренуються в читанні таблиці множення, заміні множення додаванням однакових доданків і навпаки, складання малюнків до прикладів на множення. Таблицю множення числа 2 вони заучують напам'ять. У кожного учня повинна бути картка з цією таблицею. Вони повинні знати, що 2 – це доданок (якщо приклад на множення замінюється прикладом на додавання), а 5 - число доданків. Вправи по заміні додавання рівних доданків множенням і навпаки допоможуть учням усвідомити значення 1-го і 2-го множників. Ще раз хочемо зазначити: назва компонентів дій при вивченні множення в межах 20 вчитель   вживає у своєму мовленні, але не вимагає знання цих назв від школярів.При складанні з учнями таблиці множення будь-якого числа і при її заучуванні необхідно звернути їхню увагу, що відповідь наступного приклада більша за попередній на стільки одиниць, скільки їх у 1 -му множнику. 2 x 2 = 4 2 x 3 = 6 6 – 4 = 2 2 x 4 = 8 8 – 6 = 2 2 x 5 = 10 10 – 8 = 2. Ця закономірність підкреслюється при заучуванні таблиці множення всіх чисел. Це допоможе учням швидше її вивчити. До того ж, якщо яку-небудь табличну відповідь учень не може згадати, але пам'ятає відповідь попереднього або наступного приклада, він зможе цим допомогти собі. Для кращого усвідомлення змісту множення, а також для запам'ятовування таблиці корисно вирішення виразів типу: 2 x 2 = 2 х + 2 = 14 2 х = 6 x 6 + 4 = 16 х 6 = 12 x 7 + 4 = 18 х = 8 2 х + 4 = 20 Щоб учні навчилися диференціювати дії додавання і множення, потрібно пропонувати такі вправи: 1) 2 + 2 + 2 + 2 = 8. Чи можна в цьому випадку додавання замінити множенням? Чому? 2 + 1 + 2 + 3 = 8. Чи можна в цьому випадку додавання замінити множенням? Чому? 2) Вставити у приклади потрібні знаки.  Подібні вправи змушують розумово відсталих учнів зрозуміти, що не у всіх випадках додавання можна замінити множенням, усвідомити, що множення – це додавання однакових доданків. Подібні вправи мають не лише навчальне і розвиваюче, але й корекційне значення. З множенням чисел 3, 4, 5 у межах 20 учні знайомляться аналогічно, опираючись на рахунок предметів (їхніх зображень) рівними групами. Складається таблиця додавання рівних чисел, яка потім замінюється множенням. Але вже при вивченні таблиці множення числа 3 звертається увага на те, що у вивчених таблицях є приклади з однаковими відповідями. Учні самі відшукують їх на індивідуальних картках, обводять олівцями одного кольору. Вчитель пропонує виписати першу пару прикладів (2 х 3 = 6, 3 х 2 = 6) і порівняти їх, ставлячи перед школярами такі запитання: "Яка відповідь у прикладах? Які числа множили? Яке число множили у першому прикладі? У другому? На яке число множили у першому прикладі? У другому? У чому подібність цих прикладів? У чому їх відмінність?" Назва дії ділення запозичена з латинської мови (dyvizio – поділ) загальноприйнята в західноєвропейських мовах і вживана на території України з першої половини XVIII століття. В цей же час був прийнятий і знак ділення (:). Поділити число а на число b - це значить знайти таке число х, при множенні якого на число b одержуємо число а. Ціленням називається дія, за допомогою якої за даним добутком двох співмножників і одним із цих співмножників знаходять другий співмножник. У 3-му класі допоміжної школи дія ділення в межах 20 розглядається незалежно від дії множення. Лише тоді, коли діти добре засвоять алгоритм ділення, воно зіставляється з множенням, встановлюється взаємозв'язок між цими двома діями. Досвід показує, що використання дій ділення паралельно з множенням без пояснення суті самого процесу ділення виявляється незрозумілим розумово відсталим дітям. Учні на конкретному матеріалі (операції над предметними множинами) знайомляться з діленням на рівні частини. Основний прийом ділення на рівні частини полягає у тому, що з групи предметів, які треба розділити, береться кількість предметів, які дорівнюють числу частин, щоб при діленні в кожній частині було по одному предмету, по одиниці, потім із залишку предметів даної групи знову беруть стільки предметів, щоб при діленні на дане число частин в кожній частині отримали ще по одному предмету, по другій одиниці. Так  поступають до тих пір, поки не будуть вичерпані всі предмети даної групи.Після загального ознайомлення з множенням можна переходити до пояснення ділення, починаючи з ділення числа 2, а потім ділення на дві рівні частини тощо. При діленні на 2 розкладають між двома учнями порівну зошити, ручки; кружечки; розкладають порівну на дві тарілки овочі, фрукти як натуральні, так і нарисовані, вирізані з паперу тощо. Поруч з виконанням ділення на класних посібниках учні на своїх індивідуальних посібниках розкладають вказане число предметів на потрібне число частин. Наведемо приклад: викликаються два учні і їм пропонується порівно розділити 2 олівці. Міркування проводяться так: "Візьмемо два олівці. Розділимо їх порівно на два - розкладемо порівно двом учням. Подивіться, як потрібно розділити. Один олівець даємо першому учневі, другий -другому. Чи всі олівці розділили (роздали)? Скільки олівців у кожного учня?" Записати це можна так: "Скільки було олівців? (2.) Запишемо число 2. Що робили з олівцями? (Ділили). Слово "ділити" позначається ":" (дві крапки, що ставляться одна під іншою). На скільки рівних частин ділили? (На дві рівні частини.) Запишемо число 2. Скільки отримали? (По одному). Запис 2:2=1 читати потрібно так: два розділити на дві рівні частини, отримали по одному". Учням пропонується відрахувати по два кружечки і розділити їх на дві рівні частини (розкласти на набірному полотні, покласти на два квадрати різного кольору). У зошитах школярі малюють два кружечки і ділять їх на дві рівні частини вертикальною прямою. (Роблять це за зразком, даним на дошці). Записують приклад 2:2 = 1. Потім ділять 4 предмети на дві рівні частини і записують: 4:2 = 2. Знайомство розумово відсталих учнів з дією ділення на 3 рівні частини потрібно починати з розв'язування задач, опираючись на практичні дії з предметами або на використання схем чи малюнків. Наприклад: "6 олівців роздали 3 учням. Скільки олівців отримав кожен з них?" Діти повинні спочатку розкласти олівці на 3 частини, а потім вчитель повідомляє, що це можна зробити за допомогою певного запису з використанням відомого вже знаку - ":" і ще раз зазначаємо, що ця дія називається діленням (6ол. : 3 = 2 ол.). Для закріплення цього поняття доцільно розв'язати декілька задач даного типу. Причому розв’язок повинен супроводжуватись використанням малюнків, схем, роздаткового матеріалу. Учні складають таблицю, у яку записують назви елементів під час виконання дії ділення. Таблиця 6.2.
|