Метод виклад з мат-ки 2. Спеціальна методика викладання математики зміст методика розв'язування арифметичних задач
 Скачать 7.16 Mb.
|
|
При пошуку розв'язання задачі можна використати аналітичний спосіб розбору: "Можна зразу відповісти на питання задачі: скільки коштує 2-ий і 3-ій набори чашок? (Ні) Чому не можна? (Ми не знаємо вартість однієї чашки) А скільки чашок було в 1 -ому наборі? (8 чашок) Скільки вони коштують? (24 грн.) Можемо взнати, скільки коштує 1 чашка? (Так) Якою дією? (Діленням) Отже, яким буде 1-е питання? (Яка вартість однієї чашки?) Яка перша дія? (24 грн.: 8 = 3 грн.) Якщо відомо ціну 1 чашки і кількість чашок у другому наборі, то що можна взнати? (Вартість другого набору: 3 грн. х 12 = 36 грн.) Яке третє питання? (Яка вартість третього набору) Якою дією воно розв'язується? (Множенням: 3 грн. х 10 = 30 грн.) Ми відповіли на всі питання задачі? (Так) На скільки дій ця задача? (На три) Яка її відповідь? (Вартість набору відповідно 36 грн. і ЗО грн.)" Розв'язок задачі записується у вигляді плану з конкретною арифметичною дією під кожним пунктом, або записом кожної дії з поясненням до неї. Розв'язання задачі
Відповідь: другий набір чашок коштує 36 грн., третій - 30 грн. Оскільки такі задачі мають вагоме значення у соціалізації школярів, їхньому практичному пристосуванню до життя в суспільному середовищі - роботі над ними потрібно приділяти достатню кількість уваги. Спосіб оберненого зведення до одиниці Задача: "За 3 м тканини заплатили 90 грн. Скільки метрів тканини можна купити на 210 грн. ?" Розв'язування цієї задачі зводиться до розв'язування однієї простої задачі на ділення на рівні частини, а другої - на ділення за змістом. Міркування організовується таким чином: "3 м тканини коштують 90 грн., отже, 1 м буде коштувати у 3 рази менше: 90 грн. : 3 =30 грн. Якщо 1 м тканини коштує 30 грн., то на 210 грн. можна купити стільки метрів тканини, скільки разів 30 грн. повториться у 210 грн. Щоб взнати, скільки разів це можливо, необхідно виконати дію: 210 грн. : 30 грн. = 7 (м). Відповідь: можна купити 7 м тканини". Починаючи з 7-го класу учні допоміжної школи знайомляться з задачами на рух, які розв'язуються на основі залежності між трьома величинами, які його характеризують: швидкість, відстань, час. Задачі цього типу бувають: а) на зустрічний рух; б) на рух двох тіл у протилежному напрямку; в) на рух двох тіл в одному напрямку. Ці три групи і складають основну групу задач на рух у допоміжній школі.   Розв'язування цих задач сприяє засвоєнню залежностей між швидкістю, відстанню і часом; розвиває у розумово відсталих учнів просторові уявлення. При розборі задач на рух застосовується аналітико-синтетичний метод у тій його формі, який використовується при аналізі звичайних арифметичних задач. Допомогти учням у розв'язуванні цих задач повинна графічна їх ілюстрація.Задачі на зустрічний рух Оскільки у задачі на рух беруть участь 3 величини і кожна з них може бути шуканою, то розрізняють і 3 типи задач на зустрічний рух: 1 -й тип - задачі, в яких за даною швидкістю і часом визначається шлях, 2-й тип - задачі, в яких за даною швидкістю та відстанню визначається час, 3-й тип - задачі, в яких за даною відстанню та часом визначається швидкість. Перед початком роботи над задачами цього типу у розумово відсталих дітей необхідно на конкретному прикладі з’ясувати розуміння поняття "зустрічний рух", "швидкість", "шлях". Двом учням можна запропонувати рухатись назустріч один одному - одному йти, а другому бігти. Діти наочно побачать, що у школяра, який біг, швидкість більша. І хоч до моменту зустрічі обидва були в дорозі однаковий час, другий учень подолав більший шлях, ніж перший. Для закріплення цього доцільно провести ще кілька вправ такого ж типу. Потім школярам пропонується задача: "З Луганська до Києва виїхали назустріч одна одній одночасно 2 легкові машини. Машина з Луганська проходила за годину 90 км, а з Києва – 80 км. Через 5 годин вони зустрілись. Знайти відстань між Луганськом та Києвом". Ілюстративно умову задачі краще подати у графічній формі. 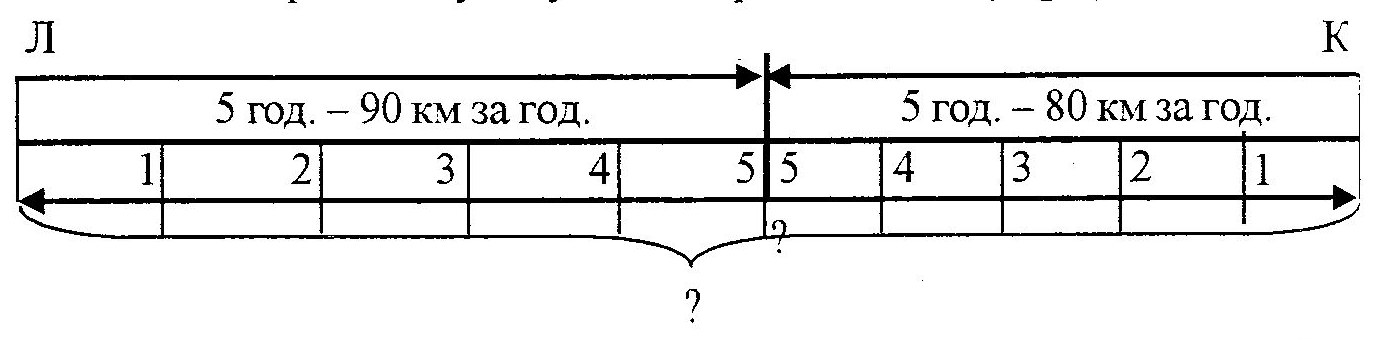 З графіка видно, що весь шлях складається з двох відрізків і що один із них більший, а другий - менший. Вчитель ставить учням питання, на які вони повинні дати відповідь: "Чи однакова швидкість машин? Скільки годин їхала машина з Луганська до зустрічі? Скільки годин їхала машина з Києва до зустрічі? З якою швидкістю їхала машина з Луганська? З якою швидкістю їхала машина з Києва? Яка машина проїхала більшу відстань? Чому? Яка меншу? Чому?" Графічна форма запису умови може привести до двох варіантів розв'язування задачі. При першому задача розв'язується 3 діями. Спочатку учні знаходять відстань, пройдену за 5 годин машиною, що виїхала з Луганська. 90 км х 5 = 450 км Другою дією знаходиться відстань, яку проїхала за 5 годин машина з Києва: 80 км х 5 = 400 км Остання дія дає відповідь на головне питання задачі: 450 км + 400 км = 850 км Відповідь: відстань від Луганська до Києва складає 850 км. Другий спосіб розв'язування задачі коротший (на 2 дії, більш лаконічно витікає з питання задачі). Першою дією учні визначають шлях, який поїдуть машини за 1 годину разом: 80км + 90км= 170 км Знаючи, через скільки годин машини зустрілися (5 год.) і шлях, пройдений ними разом за годину, можна дати відповідь на головне питання задачі: 170 км х 5 = 850 км Відповідь: відстань від Луганська до Києва складає 850 км. Другий спосіб краще застосовувати і при розв'язуванні задач, в яких потрібно за даною відстанню і швидкостями визначити час зустрічі. Задачі, є яких за даними шляхом та швидкістю визначається час Задача: "З Києва і Одеси, відстань між якими 500 км, одночасно виїхали назустріч один одному 2 автобуси. Швидкість одного з них 75 км за год., а другого - 50 км за год. Через скільки годин автобуси зустрінуться?" Зробимо короткий запис у графічній формі:    При розборі умови задачі виявляється, що до зустрічі автобуси повинні проїхати всю відстань від Києва до Одеси. Київський автобус пройде відстань від К до місця зустрічі, а одеський - від О до місця зустрічі. Оскільки київський автобус їде швидше, то і відстань він проїде більшу, аніж автобус з Одеси. Для того, щоб відповісти на головне питання задачі, потрібно визначити відстань, яку автобуси проходять за 1 годину разом. Якщо автобус з Києва рухається зі швидкістю 75 км/год, а з Одеси - 50 км/год, то разом вони за годину проходять75 км + 50 км =125 км Таким чином, через кожну годину вони наближаються одне до одного на 125 км і щоб визначити, через скільки годин обидва автобуси зустрінуться, необхідно визначити, скільки разів 125 км міститься у 500 км. 500 км : 125 км = 4 План і розв'язок даної задачі буде таким: 1. Скільки кілометрів проходять обидва автобуси за годину 75 км + 50 км =125 км 2. Через скільки годин автобуси зустрінуться? 500 км : 125 км = 4 год. Відповідь: автобуси зустрінуться через 4 години. Задачі, в яких за даним шляхом і часом визначається швидкість Задача: "Від Києва до Москви 850 км. З цих міст одночасно назустріч одне одному виїхали 2 автобуси. Київський автобус їхав зі швидкістю 80 кілометрів за годину. З якою швидкістю їхав московський автобус, якщо вони зустрілися через 5 годин?" Проілюструємо задачу у графічній формі: 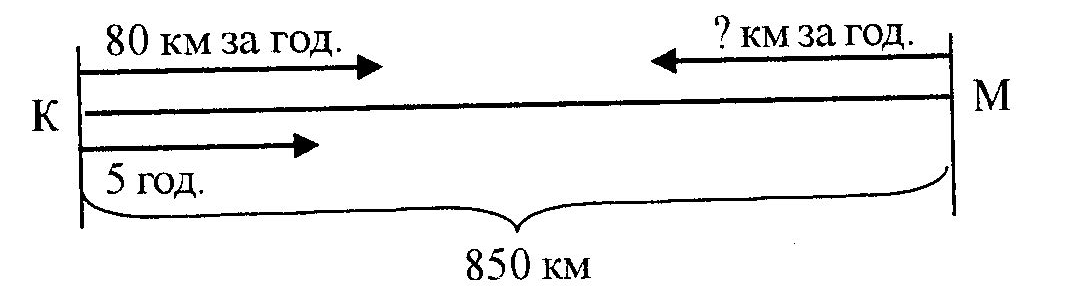 Починається робота над такою задачею зі звертання уваги школярів на те, що автобуси рухалися назустріч одне одному 5 год. і зустрілися в точці Б. З’ясовується відстань між Києвом і Москвою(850 км). Вчитель просить учнів відповісти на запитання: "Маючи такі дані, як кількість годин, пройдених до зустрічі київським автобусом і його швидкість за годину, що можна визначити? Якою арифметичною дією?" Учні складають перший пункт плану і записують відповідну арифметичну дію: 1. Скільки км проїхав київський автобус за 5 годин? 80 км х 5 = 400 км Для відповіді на головне питання задачі необхідно знати шлях, який проїхав московський автобус за 5 годин. Нам відома відстань, яку проїхав київський автобус за 5 годин, відома відстань від Києва до Москви (850 км). Учням пропонується поставити друге питання задачі та його розв'язок. 2. Скільки кілометрів проїхав московський автобус за 5 годин? 850 км – 400 км = 450 км Оскільки він проїхав 450 км, а їхав він 5 годин, тепер можна відповісти на головне питання задачі: 3. Яка швидкість московського автобуса? 450 км : 5 = 90 км Відповідь: московський автобус їхав зі швидкістю 90 км за год. Задачі на рух 2-х тіл у протилежних напрямках Задачі цього типу бувають різної складності. Для розумово відсталих учнів найбільш легким і доступним є той тип, де з одного і того ж пункту виходять одночасно і рухаються у протилежному напрямку, причому шуканим є відстань між цими тілами через рівний проміжок часу. Наприклад, задача: "Від пристані відійшли 2 пароплави у протилежних напрямках. Один плив зі швидкістю 30 км за год., а другий - 35 км за год. На якій відстані один від одного будуть ці пароплави через 3 год. після свого виходу? Проілюструємо умову задачі: 35 км. за год. П 30 км. за год.     3 год. 3 год.Під час роботи над задачею вчитель звертає увагу учнів на її особливості використовуючи систему навідних запитань: "Скільки     було пароплавів? Звідки вони випливали? У якому напрямку? Яка швидкість першого пароплава? Яка швидкість другого пароплава? Що потрібно знайти в задачі?"Після розбору умови задачі і складання плану учням пропонується записати її розв'язок двома способами. Перший спосіб: 1. Скільки кілометрів проплив перший пароплав за 3 год.? 30 км х 3 = 90 км 2. Скільки кілометрів проплив другий пароплав за 3 год.? 35 км х 3 =105 км 3. На якій відстані один від одного будуть пароплави через 3 год. після свого виходу? 90км + 105 км = 195 км Відповідь: відстань між пароплавами буде 195 км. При розв'язуванні задачі другим способом перш за все потрібно звернути увагу школярів на швидкість, яку кожен пароплав проходить за годину, після чого запитати у них, на якій відстані пароплави будуть один від одного через годину і якою арифметичною дією можна відповісти на це питання? Якщо відома відстань від одного до іншого пароплава через годину їхнього плавання, чи можна відповісти на головне питання задачі? Як це зробити? Учні записують план і розв'язок задачі: 1. На якій відстані будуть пароплави один від одного через годину? 30 км + 35 км = 65 км 2. На якій відстані вони будуть між собою через 3 год.? 65 км х 3 = 195 км Відповідь: відстань між двома пароплавами 195 км. Розв'язуючи будь-який тип задачі, потрібно звертати увагу учнів на те, що яким би способом не була знайдена відповідь, вона має бути завжди однакова. При можливості розв'язування задачі двома способами завжди обирають більш раціональний. Задачі на рух двох тіл в одному напрямку Розумово відсталим учням краще пропонувати задачі, у яких рух починається одночасно з різних пунктів, які лежать на одній прямій. Наприклад, задача: "З пункту А виїхав велосипедист зі швидкістю 12 км за год. В той же час з пункту Б вийшов пішохід зі швидкістю 4 км за год. Обидва рухаються в одному напрямку. Через скільки годин велосипедист дожене пішохода, якщо відстань від пункту А до пункту Б - 24 км?" Проілюструємо задачу: 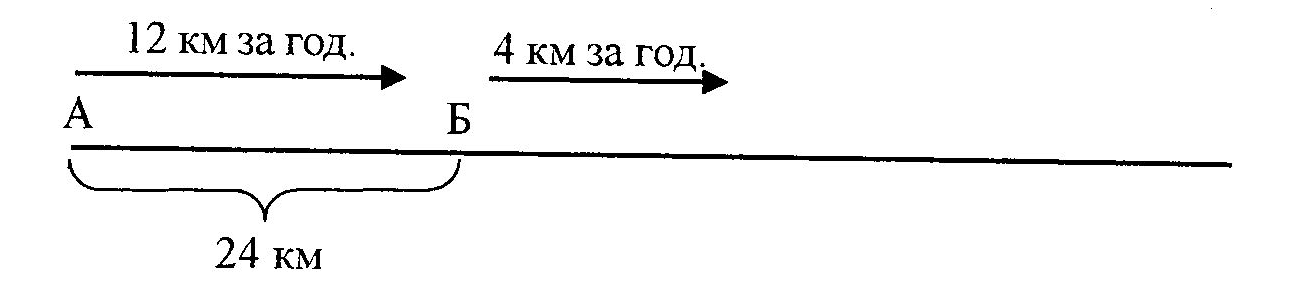 При розборі задачі необхідно звернути увагу на те, що швидкість велосипедиста більша за швидкість пішохода. Отже, перший дожене другого, оскільки через кожну годину велосипедист наближається до пішохода на8км (12км-4км = 8 км). Якщо відстань між ними 24 км, а наближається один до другого за годину на 8 км, то можна взнати, через скільки часу буде подолана вся відстань між ними? План і розв'язок задачі 1) На скільки кілометрів велосипедист за годину наближається до пішохода? 12км – 4км = 8км 2) Через скільки годин велосипедист дожене пішохода? 24 км : 8 км = 3 Відповідь: велосипедист дожене пішохода через 3 години. Контрольні запитання.
    Рекомендована література.
2. Усна лічба на уроках математики в допоміжній школі 2.1. Значення усної лічби для учнів допоміжної школи Поряд з формуванням основних математичних понять, вивченням властивостей чисел і законів арифметичних дій важливе місце в допоміжній школі займає формування в учнів обчислювальних навичок. Складовою частиною майже кожного уроку математики є вправи з усної лічби. їх значення надзвичайно велике. Учні у процесі рахування вдосконалюють навички усної лічби, краще запам'ятовують назви чисел, компоненти і закони арифметичних дій, розвивають вміння у розв'язанні простих і складених задач, оволодівають математичною термінологією. Усна лічба вносить різноманітність у викладання математики, сприяє закріпленню знань і дає можливість швидко перевірити їх. Оволодіння учнями зі стійкими інтелектуальними вадами обчислювальними навичками готує їх до більш швидкого проведення цих обчислень у процесі трудової діяльності у шкільній майстерні, при відвідуванні магазинів, пошти тощо. Вміння швидко і правильно робити в повсякденному житті обчислення мають практичну значущість для вихованців допоміжної школи. Для того, щоб зробити усні обчислення не вдаючись до докладнішого запису, учні повинні зосередити свою увагу на пропонованих завданнях, запам'ятати числа і результати. Для виконання будь-якої арифметичної дії учневі необхідно використати найбільш раціональний шлях розв'язання. Він можливий лише при використанні таких мисленнєвих процесів, як аналіз, синтез, узагальнення. Все це сприяє як розвитку пізнавальних здібностей учнів, так і подоланню їх недоліків. Здійснюючи розв'язання прикладів і задач усно, учні розвивають математичну мову, збагачуючи її математичними символами, розширюючи словниковий запас. Вони запам'ятовують математичні терміни, вирази, вчаться ясно і лаконічно висловлювати свої судження, хід розв'язання задач та обчислення прикладів. Використовуючи багаторазове повторення обчислення арифметичних прикладів та розв'язування задач, які подаються у цікавій формі, з використанням різноманітних засобів, школярі безпо    середньо переконуються у їхньому практичному значенні. Учень, який на достатньому рівні оволодів навичками усного рахунку більш самостійний на уроках ручної праці, трудового навчання, географії, природознавства тощо, значно легше включається у різноманітну трудову діяльність, яка є невід'ємною складовою його повсякденного життя, а, отже, і соціалізації в цілому. Так само легше він оволодіває професійною підготовкою, оскільки вміння швидко виконувати усні обчислення є невід'ємною складовою будь-якої професійної діяльності.Вправи з усної лічби створюють емоційно позитивну ситуацію на уроках математики, викликають інтерес з боку учнів не тільки до них, але й до предмету в цілому. Вони урізноманітнюють уроки математики і роблять їх цікавими для школярів. Не менш важливе значення усного рахунку для формування у розумово відсталих школярів таких якостей, як вміння усвідомлено і цілеспрямовано працювати розумово, вміння швидко орієнтуватись у поставленому завданні, вибирати найбільш ефективні шляхи для точного і правильного його виконання. Необхідність зосередити зусилля, щоб запам'ятати числа, вказані арифметичні дії, виконати ланцюжок інтелектуальних операцій і довести розпочату роботу до кінця, отримавши вірну відповідь – все це сприяє розвитку логічного мислення у школярів, уваги, пам'яті та інших психічних процесів. Таким чином, усна лічба має велике як освітньо-виховне, так і корекційно-практичне значення для учнів з особливими потребами у навчанні. Але при цьому потрібно зазначити, що не всі вказані якості, які виховуються і формуються на заняттях з усного рахунку, стають можливими і доступними для використання розумово відсталими школярами навіть в тому випадку, коли вчитель досконало володіє методикою їхнього проведення, використовує їх систематично, з тонким урахуванням індивідуальних психофізичних можливостей учнів допоміжної школи і завдань їх корекції. В структурі уроку вчитель чітко визначає мету усної лічби як окремого етапу уроку, і відповідно до неї підбирає види вправ та форму їх проведення. Його метою може бути:
Навчання обчислювальній техніці необхідно здійснювати на основі застосування відповідних форм, прийомів та спеціально підібраних вправ з усної лічби. |