Метод виклад з мат-ки 2. Спеціальна методика викладання математики зміст методика розв'язування арифметичних задач
 Скачать 7.16 Mb.
|
|
2.3. Види вправ з усної лічби Щоб заняття усної лічби були цікавими, викликали активність і уважність дітей, вони повинні бути різноманітними. Доцільно використовувати наступні види усних вправ. 1. Прості приклади - приклади на одну дію. Вони пропонуються учням протягом всіх років навчання у допоміжній школі. Величина чисел (цілих і дробових), з якими складаються приклади, визначаються програмою з математики для кожного класу. Приклади можуть пропонуватись в різній формі: а) вчитель називає арифметичну дію, яку діти повинні зробити над запропонованими числами. Наприклад: "Порахуйте, скільки буде, якщо 8 помножити на 3?" б) вчитель називає результат, який учні повинні отримати, вказуючи арифметичну дію у непрямій формі. Наприклад: "Назвіть суму чисел 12 і 7". в) учням пропонується розв'язати приклади на збільшення або зменшення числа на кілька одиниць або в кілька разів. Наприклад: "Збільшити число 5 на дві одиниці", "Зменшити число 20 у 5 разів". Учитель диктує приклад або задачу всьому класу у такому темпі, щоб учні встигли зробити обчислення. 2. Складні приклади - приклади на дві і більше дій або з однією дією, але з кількома компонентами. Розв'язання таких прикладів викликає деякі труднощі в учнів. Вони викликані тим, що школярі повинні утримувати в пам'яті проміжні результати і називати тільки відповідь. Деякі учні не здатні утримувати в пам'яті ці результати, що призводить, в кінцевому результаті до помилкового обчислення прикладу. Тому таким учням можна дозволити записувати проміжні результати, використовувати додатковий дидактичний матеріал. Пропонуючи складні приклади, слід читати кожну дію окремо в тій послідовності, в якій вона повинна бути виконана. Після оголошення кожної дії вчитель робить паузу. Тривалість її повинна бути такою, щоб учні змогли виконати обчислення. По мірі розвитку навичок швидкої лічби паузи між діями робляться коротшими. Але дуже короткі паузи можуть призвести до того, що учні не встигнуть здійснити розв'язання прикладу. Після закінчення останньої паузи вчитель задає питання усьому класу: "Яке число отримали?" Запитати відповідь необхідно у 2-3 учнів. Потім педагог звертається з питанням до всього класу: "У кого не така відповідь?" і вияснити причину помилки. 3. Самостійне складання прикладів. Для розвитку самостійності, любові до математики учням допоміжної школи пропонуються не тільки приклади у готовому вигляді, але й надається можливість їх складати. Вони вчаться утворювати як прості, так і складні приклади. Однак спонтанно розумово відсталі діти не можуть цього зробити. Цьому їх необхідно вчити. Виправдала себе наступна послідовність пояснення прийомів складання прикладів.   При складанні простих прикладів:а) учням пропонується складання прикладів з використанням наочності та дидактичного матеріалу; б) учні складають приклади з числами і діями, які вказав учитель. Наприклад: "Складіть приклади на додавання з числами 10 і 2"; в) вчитель вказує ту арифметичну дію, яку учні повинні виконати. Наприклад: "Складіть приклад на додавання"; г) складання прикладів за числами без вказування арифметичної дії. Наприклад: "Які приклади можна скласти з числами 25 і 5?" При утворенні складних прикладів вчитель може використовувати наступні прийоми в такій послідовності: а) складання прикладів на наочній та дидактичній основі; б) складання прикладів без застосування будь-яких додаткових засобів; в) складання прикладів з трьох і більше компонентів на знаходження суми, різниці, добутку, частки; г) складання прикладів на всі арифметичні дії з даною відповіддю. Наприклад: "Складіть складний приклад на три різних дії з відповіддю ЗО." 4. Кругові приклади. Це такі приклади, у яких відповідь попереднього приклада є початком наступного, а відповідь останнього - початком першого. При навчанні складанню таких прикладів розумово відсталих учнів необхідно дотримуватись певної послідовності. 1) На першому етапі ознайомлення учитель сам складає готові приклади, а їх обчислення здійснюється разом з учнями. Наприклад: 17 + 3=..., 20:4=..., 5x6=..., 30–13=... Під час їхнього обчислення педагог звертає увагу школярів на те, що відповідь першого приклада є початком другого, відповідь другого – початком третього, а відповідь останнього - початком першого. Після чого він повідомляє учням, що такі приклади називаються круговими. 2) Коли діти зрозуміли сутність утворення таких прикладів учитель ускладнює умову їхнього обчислення. На наступному етапі дітям пропонується часткове складання кругових прикладів. У цьому випадку вихованцям пропонується перший приклад, а в останніх вказуються дії і другий компонент: 17 + 3 = ..., ... :4 = ..., ...х6 = ..., ...-13=.... 3) На наступному етапі учні складають приклади за вказаними діями. Перший приклад дається вчителем: 17 + 3 = ..., ...:... = ..., ...х... = ..., ...–... = .... 4) На останньому етапі навчання складанню кругових прикладів учням надається повна самостійність. Для школярів з меншими пізнавальними можливостями можна дати перший приклад (17+3=...). 5. Дидактичні ігри і цікаві вправи. Розумово відсталі діти люблять гру, хоч і не завжди розуміють її значення. Це бажання і потребу необхідно використати на уроках математики і направити на розв'язання тих навчальних задач, які стоять перед уроком. У процесі гри можна використовувати навчальні посібники, іграшки, дидактичний матеріал. Необхідно, щоб цей вид вправ носив не тільки навчальний, але й виховний характер. Дидактичні ігри та цікаві вправи сприяють більш плавному і менш помітному переходу учнів від ігрової діяльності до серйозної навчальної роботи, а позитивні емоції, які виникають під час гри, активізують увагу учнів, стимулюють їх до активної діяльності, забезпечують вирішення задач, які пов'язані з розвитком пам'яті, мовлення та інше. Гра може проводитися як індивідуально, так і колективно. При індивідуальній роботі завдання необхідно давати з урахуванням розумових можливостей і здібностей учня. У допоміжній школі добре відомі такі ігри, як "Драбинка", "Мовчанка" та інші. Вчитель може використати при проведенні ігор і наочні посібники. Наприклад: "Множення числа 4" "Число 15 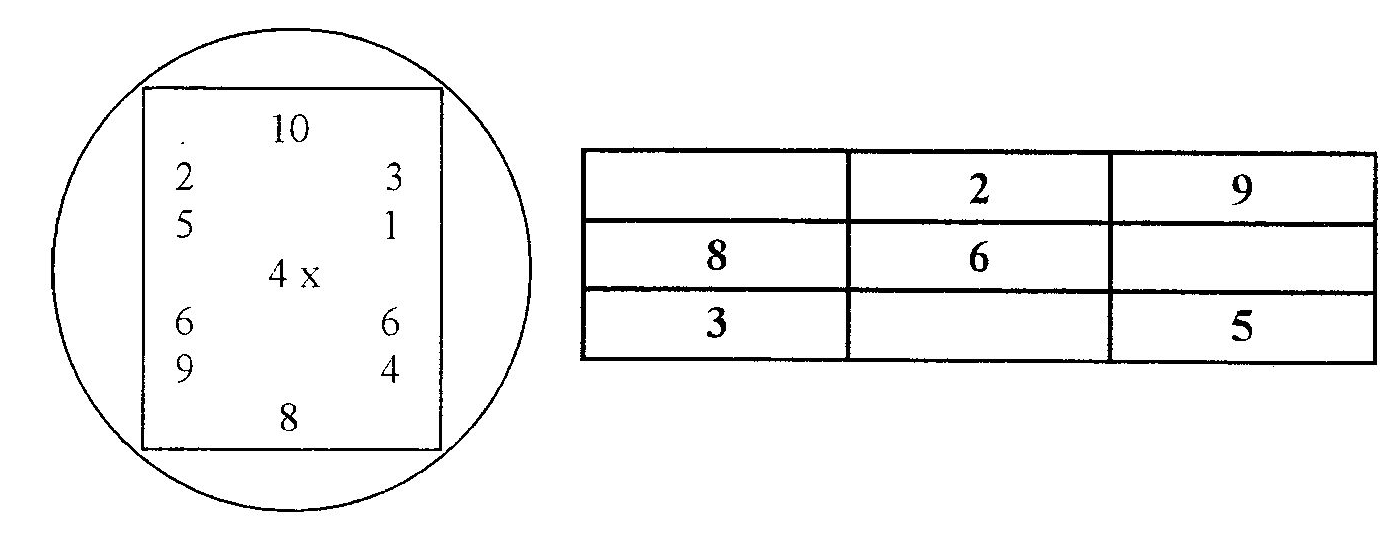 6. Надзвичайно велике значення з розвитку уваги, пам'яті, логічного мислення відіграють усні задачі. їхнє розв'язування проводиться майже на кожному уроці математики. Слід відзначити, це найбільш складний і відповідальний розділ у курсі математики. В той же час задачі несуть у собі велику корекційно-освітню роль. Вони розширюють знання учнів про навколишній світ, сприяють більш успішному оволодінню професійною працею, розвивають основні психічні процеси. При розв'язуванні арифметичних задач усно учні допоміжної школи краще розуміють ситуацію, викладену в ній, залежність між даними і шуканим, логічний зв'язок між питанням і даними і перевести функціонально-кількісні відносини в план арифметичних дій. Найбільш поширеними простими задачами, які пропонуються учням допоміжної школи, є задачі на: а) знаходження суми: "В одному ящику 10 кг яблук, у другому - 15 кг груш. Скільки всього кілограмів фруктів у двох ящиках?" б) знаходження залишку: "315 м тканини 10 м пішло на виготовлення костюмів. Скільки метрів тканини залишилось?" в) знаходження добутку: "В одному пакеті 2 кг борошна, а в другому - в 5 разів більше. Скільки кілограмів борошна у другому пакеті?" г) знаходження частки: "12 м тканини поділили на три однакових відрізи. Скільки метрів тканини в одному відрізі?" ґ) з застосуванням графічних вмінь: "Між двома містами 5 залізничних станцій. Потяг пройшов 2 зупинки. Скільки станцій залишилось пройти потягу?" 5 зупинок 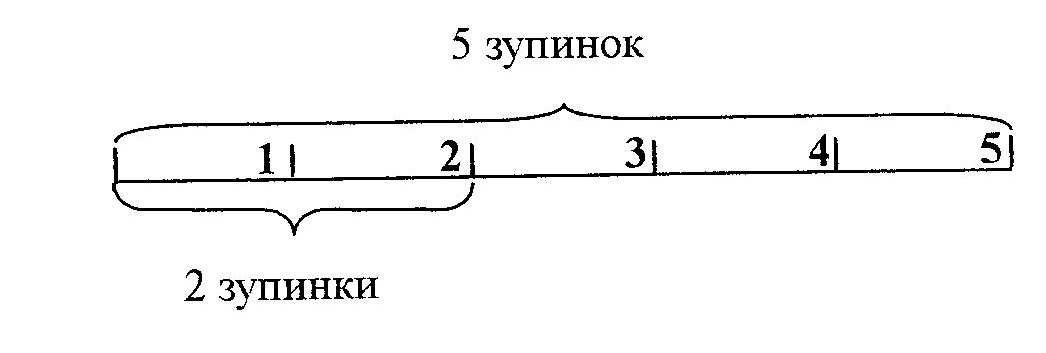 д) за запропоновано наочністю придумати питання задачі: 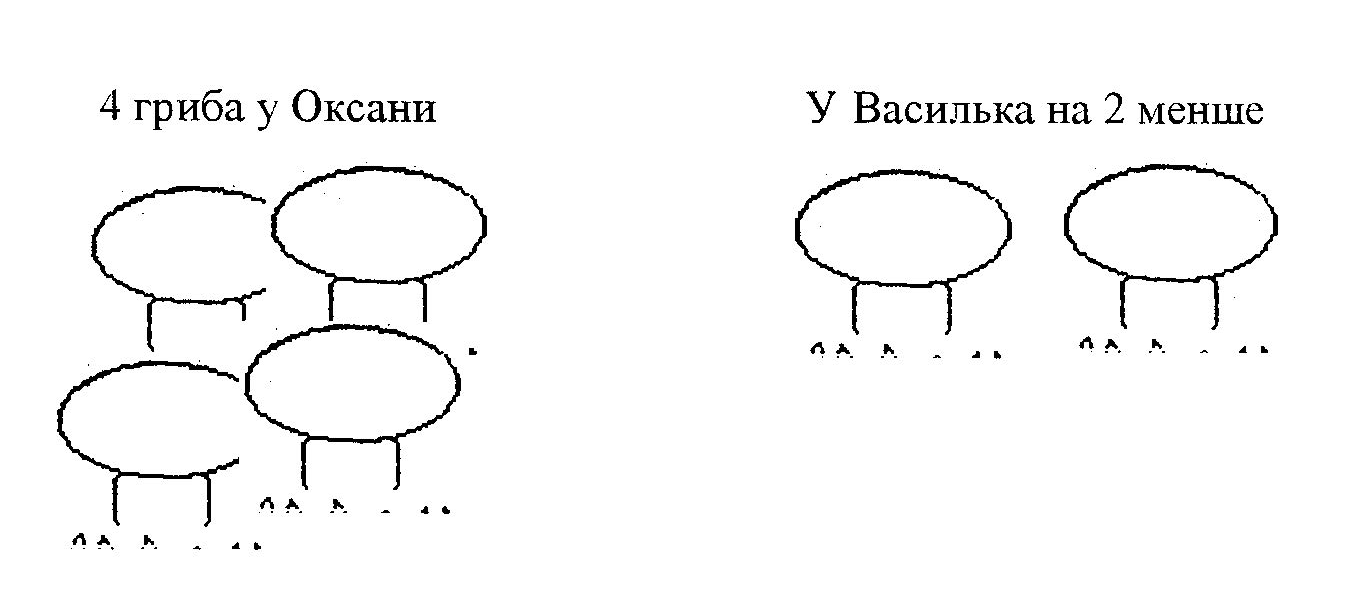 Питання: На скільки у Василя грибів менше?
є) з використанням таблиць:
7.3 метою обліку сформованих навичок обчислень використовуються арифметичні диктанти. Вони проводяться у кожному класі і дають можливість перевірити знання учнів з усної лічби за короткий час, оскільки діти пишуть тільки відповіді. Для цього вчитель підбирає 4-6 у молодших, та 6-8 у старших класах вправ з вивченого матеріалу. Кожне завдання читається 1-2 рази, а учні записують відповіді в зошитах або на окремих аркушах. Наприклад, математичний диктант для учнів 4-го класу допоміжної школи: 1. Запишіть числа, які складаються з 3 десятків і 3 одиниць. Запишіть сусідні числа 99. Відніміть від 100 число 20. Помножте число 7 на 5.
   2.4. Організація занять усною лічбоюУ структурі уроку вчитель математики виділяє час для усної лічби і визначає її мету. Мета усних обчислень визначає і її місце на уроці. Якщо метою усної лічби є знайомство учнів з новими прийомами обчислень, їх закріплення або вироблення навичок швидкої лічби, то його краще всього проводити на початку уроку, після перевірки домашнього завдання. Якщо ж усна лічба ставить за мету підготувати учнів до сприймання нового матеріалу, то його треба проводити перед поясненням, у середині уроку. При тривалій і одноманітній роботі, коли учні проводять практичну, лабораторну або самостійну перевірочну роботу їх необхідно переключити з одного виду роботи на другий. У таких випадках їм краще запропонувати усну лічбу в кінці уроку у вигляді дидактичних ігор, цікавих вправ. Розумово відсталі учні дуже повільно оволодівають прийомами усної лічби. Тому при підборі вправ учитель керується принципом диференційованого та індивідуального підходу до учнів. Для одних дітей завдання може бути складним, для других - простішим; одним достатньо пред'явити їх на слух, а для інших треба використати і зоровий, і кінестетичний аналізатори. Усну лічбу обов'язково треба оцінювати, а в старших класах і з виставленням оцінки в журналі. Вчитель може виконувати як індивідуальну, так і фронтальну форму контролю знань учнів з усної лічби. При фронтальній формі він слідкує за активністю класу, правильністю відповідей. При індивідуальному опитуванні педагог має можливість більш глибоко виявити знання учнями прийомів усної лічби, правил, математичного словника тощо. Тривалість проведення вправ з усної лічби - 5-10 хвилин. Контрольні запитання.
Рекомендована література.
   3. Методика вивчення 1-го десятка3.1. Причини виділення першого десятка в окремий концентр Вивчення чисел першого десятка і дій над ними є основою формування в учнів допоміжної школи цілісної системи математичних знань, умінь та навичок. Без чіткого усвідомлення цього матеріалу переходити до наступних концентрів просто фізично неможливо і тому цьому розділу приділяється значна увага. Розглянемо причини виділення першого десятка в окремий концентр.
3. Арифметичні дії в межах першого десятка за своїми прийомами різко відрізняються від дій, які вивчаються на наступних етапах вивчення математики.
Організація роботи з розумово відсталими школярами над числами першого десятка вимагає врахування основних завдань цього курсу.
4. Ознайомлення:
3.2. Нумерація чисел в межах 1-го десятка У 1-му класі допоміжної школи учні починають вивчати нумерацію – сукупність прийомів називання і позначення чисел з допомогою слів-числівників (усна нумерація) і допоміжних знаків (письмова нумерація). Як ми вже зазначали раніше, у допоміжну школу приходять розумово відсталі діти з різним рівнем готовності до засвоєння математичних понять. Ті з них, які прийшли зі спеціалізованого дитячого садка або з сімей, які опікувались ними, вже мають первинні уявлення про кількість, число, в них наявні елементарні навички рахунку. Інші ж школярі, які потрапляють у заклад з сімей з несприятливим кліматом для виховання, з загальноосвітніх шкіл та дошкільних закладів, в більшості випадків не мають таких навичок. Але основне завдання вчителя - навчити розумово відсталих рахунку та обчислювальним   операціям - залишається актуальним для будь-якої групи школярів. Тому постає проблема визначити актуальний рівень математичних знань, які мають учні. Для цього в допоміжній школі є пропедевтичний період, на який в залежності від необхідності дається від 2-х тижнів до 1-го місяця. Про форму організації роботи в цей період ми пояснювали на попередніх лекціях.Методичними розробками по організації вивчення розумово відсталими учнями чисел і цифр в межах першого десятка займались В.І. Басюра, Н.Д. Богданович, К.Г. Кущ, Н.І. Непомняща, М.М. Перова, В.В. Єк та інші. Вони визначили певну послідовність роботи над цим матеріалом. Під час ознайомлення школярів з кожним числом 1-го десятка розглядається його утворення шляхом прилічування одиниці (крім числа і цифри 1), відлічування одиниці з наступного, позначення його цифрою, прямим і оберненим рахунком у межах цього числа, співвідношення предметної сукупності, числа і цифри, визначення місця числа в натуральному ряді. При цьому числа порівнюються, вивчається їхній склад, відрізок числового ряду, з ними виконуються дії додавання і віднімання, розв'язуються прості арифметичні задачі на знаходження суми і залишку. Головне завдання, яке стоїть перед вчителем у 1-му класі – сформувати у розумово відсталих навички рахунку: вони повинні вміти перераховувати предмети у межах першого десятка, відраховувати меншу кількість елементів від більшої, утворювати множину з двох менших, усвідомлювати, що коли до множини прибавляються предмети - вона стає більшою, зростає; якщо з неї забираються предмети - стає меншою. Значна увага приділяється розвитку вміння порівнювати множини різними способами (шляхом встановлення взаємооднозначної відповідності, перелічуванням, в умі), формуванню навичок переходу від порівняння множин предметів до порівняння чисел, які позначають кількість елементів даних множин. Учні 1-го класу допоміжної школи знайомляться з числівниками, які використовуються для позначення чисел, в них формується усвідомлення їхнього значення стосовно тієї кількості, яку вони позначають. Потрібно зазначити, що саме практичні дії з конкретними предметами сприяють формуванню початкових уявлень про число. Тому вчитель повинен бути забезпечений якомога більшою кількістю наочних посібників, з якими працюють учні. На сучасному етапі розвитку суспільства все більше в навчальну діяльність входять такі технічні засоби, як комп'ютер, відеомагнітофон, диктофон тощо. Відомо, що формування поняття числа у дітей проходить складний шлях: спочатку утворюються елементарні уявлення про множину, яку позначають числом, потім про кількість конкретних предметів, які стоять за числом, надалі поступово виділяються суттєві ознаки числа і відбувається відмежування числа від предметів і його Узагальнення. У своїх дослідженнях М.М. Перова1, К.Г. Кущ2 та інші виділили основні труднощі, які спостерігаються у розумово відсталих при вивченні нумерації чисел у межах 10. Так, учні, які прийшли в 1-й клас допоміжної школи, як правило, знають назви кількісних числівників у певному порядку в різних межах, але нерідко відмовляються рахувати або допускають багато помилок під час рахунку предметів, які раніше не використовувалися як об'єкти рахунка, особливо якщо вони даються в незвичному для них положенні в просторі або на площині (наприклад, розташовані вертикально, похило, врозкид). Тому при визначенні числа предметів потрібно їх вчити абстрагуватись від форми їх розміщення, величини тощо. Деякі школярі не усвідомлюють, звідки потрібно почати рахунок. Багато хто з них думає, що рахувати предмети в горизонтальному положенні можна лише зліва направо. Якщо їх просять перерахувати предмети навпаки - вони їх не рахують, а просто промовляють усі числа від 10 до 1. Це свідчить про стереотипно заучений числовий ряд без розуміння суті рахунка. Наслідком цього є і невміння рахувати від будь-якого заданого числа. Як правило, розумово відсталі учні, якщо їх не навчити варіантам рахунка, можуть рахувати лише від одиниці. Вони також відчувають труднощі при відповіді на запитання "Скільки?". Кожного разу починають перераховувати предмети, але не повідомляють результат рахунка. Тому це обов'язково потрібно враховувати вчителю на уроках і ставити учневі, який відповідає, такі запитання, які б передбачали об'єднання множини.  Значні труднощі спостерігаються при визначенні загальної кількості неоднорідних предметів. Першокласники окремо перераховують кожну групу однорідних предметів, не поєднуючи їх у загальну сукупність. Інколи навіть незначна різниця в кольорі і розмірі є перешкодою до об'єднання їх в одну множину. Але в той же час використання для рахунку предметів однакової величини, кольору, форми протягом усього часу затримує розвиток у розумово відсталих арифметичних понять. Тому, проводячи такі заняття, вчитель повинен рахувати якомога більшу кількість предметів, постійно використовувати для цього нові, рахувати різні предмети. Головне завдання, яке стоїть при цьому перед ним - домогтись усвідомлення учнями того, що числом можна позначити будь-яку множину, причому вона може містити у собі не лише однорідні предмети.Розумово відсталим важко дається вміння співвідносити число і відповідний предмет. У значної частини школярів не сформовано розуміння різниці між кількісним і порядковим рахунком: у відповідь на завдання показати 5 предметів учень показує п'ятий по рахунку. Ці недоліки призводять до поганого розуміння учнями числового ряду, співвідношення кількості і числа. Потрібно також зазначити, що в більшості учнів допоміжної школи наявні порушення дрібної моторики руки, в окремих з них є патології розвитку опорно-рухового апарату в цілому у вигляді паралічів, парезів, гіперкінезів. Тому від вчителя вимагається враховувати ці відхилення і організовувати відповідним чином роботу на уроках: використовувати наочність достатньої величини, технічні засоби, організувати індивідуальну допомогу тощо. На основі аналізу наукової літератури нами було визначено, що для засвоєння математичних знань, умінь та навичок є важливою номінативна організуюча та регулююча функції мовлення. Через наявність у розумово відсталих школярів значного недорозвитку цих функцій мовлення у них виникають труднощі запам'ятовування чисел. Часто вони через наявні порушення не можуть назвати число ні спонтанно, ні репродуктивно. Особливі проблеми викликають числа, які починаються з опозиційних звуків, наприклад: "сім - вісім", "шість - сім", "п'ять - дев'ять". Також проблеми виникають при диференціації чисел, якщо ті даються для розрізнення парами. У числах, де є збіг приголосних, у школярів, як правило, один з звуків пропадає (при називанні числа "два" у них пропадає звук "д"). Організовуючи роботи з учнями першого класу, необхідно мати достатню кількість наочних посібників, адже практично кожне нове число або математичне поняття, яке ми формуємо у школярів, потрібно унаочнити. Наочність грає велике значення не тільки в пізнавально-освітньому, а й у корекційно-розвиваючому плані. Тому доцільно показати наочні посібники, які використовуються в процесі роботи і розкрити основні вимоги до них. На уроках математики в допоміжній школі застосовується така наочність.
Наочні посібники та дидактичний матеріал на цьому етапі навчання повинні відповідати наступним вимогам.
7.При демонстрації об'ємної наочності учні повинні мати можливість розглянути її з усіх боків. 8. Наочні прилади повинні бути легкорухомими, щоб їх можна було розташувати на площині у будь-якому порядку. Розглянемо основні етапи роботи над вивченням нумерації чисел в межах 10. 1. Знайомство з числом, кількістю і цифрою. Потрібно сказати, що поняття числа відноситься до досить абстрактних, адже само по собі число не існує у будь-якому предметі: "не існує трьох столів, на які ми дивимось, є лише стіл, стіл і стіл, і ми подумки охоплюємо їх як щось єдине, як три. Число це є unitas mentalis unitatum multiplisium (багато, про яке думаємо як про одне)"1. Поняття числа у дітей формується складним шляхом – спочатку утворюються елементарні уявлення про множину, яку позначають певним числом, потім про кількість конкретних предметів, які стоять за числом, далі поступово виділяється суттєва ознака числа і відбувається його узагальнення. П.Я. Гальперін виходить з розуміння числа як відображення кількісних відношень між множиною і прийнятою мірою, величина якої непостійна і залежить від тих предметів, над якими виконується вимірювання. Число, таким чином, виступає не як простий знак, а є предметом дії. Він доводить, що формування всіх розумових дій проходить ряд етапів від наочно-дійової форми до узагальнюючої, яка виконується подумки через перехід від розгорнутої за складом операцій форми до стислої, від довільної за протіканням до автоматизованої. При вивченні будь-якого числа з розумово відсталими учнями вчитель повинен використовувати достатню кількість наочних посібників. Без цього формування у них усвідомлених дій оперування числами, цифрами і відповідними множинами, які вони позначають, буде просто неможливо. У роботі над кожним числом першого десятка потрібно дотримуватись певної послідовності: рахунок предметів множин, чисельність яких характеризується розглядуваним числом; співвіднесення числа з відповідною цифрою; утворення нового числа з попереднього через прилічування одиниці; утворення попереднього числа через відлічування одиниці; співвіднесення кількості предметів, числа та цифри; порівняння чисел між собою; рахунок в межах даного числа; написання відповідної цифри. Починати знайомство з числами потрібно через рахунок предметів і утворення нової множини шляхом прилічування одиниці. Вивчаючи будь-яке число в межах 10, вчитель пояснює його утворення через додавання ще одного предмета до вже вивченої множини ("Ми вже вивчили число 2. А якщо до двох червоних кружечків, які я виставив у набірному полотні, приставити ще один зелений, ми отримаємо нове число. Яке отримаємо число?").   2  13 Після формування усвідомлення нової множини і позначення її відповідною цифрою потрібно пояснити учням, що попереднє число, тобто 2, може утворитись і шляхом відлічування: "Якщо від трьох кружечків забрати один, яке число утвориться?" Отже, до кінця 1-го класу учні повинні розуміти, що кожне число першого десятка утворюється з попереднього шляхом додавання одиниці, а якщо від даного числа відлічити одиницю - отримаємо попереднє число. Цим ми підводимо розумово відсталих дітей до розуміння II і III властивостей числового ряду: будь-яке натуральне число (крім 1) йде за попереднім числом (є його "правим" сусідом);  будь-яке натуральне число передує наступному (є його "лівим" сусідом).У 1-му класі допоміжної школи школярі знайомляться з тим, що числа можна отримувати не лише в результаті рахунку, але й внаслідок вимірювання. Для цього доцільно використовувати лінійку (як ми вже вказували раніше, лінійка з нанесеною на ній сантиметровою шкалою є гарним наочним посібником при розгляді питань нумерації, зокрема, отримання чисел, і бажано, щоб вона мала довжину 10 см). Використовуючи лінійку, ми утворення кожного числа закріплюємо через знайомство з відповідною мірою довжини. Досить цікавим і ефективним посібником для навчання розумово відсталих є монети вартістю 1 коп., 2 коп., 5 коп., 10 коп. Вони вже знають, що за гроші можна купити ту чи іншу річ і тому з цікавістю ставляться до роботи з ними. Отже, використання монетної каси є необхідною передумовою формування і усвідомлення першокласниками значення числа. Під час вивчення 1 потрібно звернути увагу, що одиниця є першим числом, яке позначає певну множину або предмет (натуральне число) і тому не йде ні за яким числом, тобто не є, виходячи з порядкової теорії Д. Пеано (1858-1932), яку він вибудував на аксіоматичній основі, його "правим" сусідом. Це є перше натуральне число. У допоміжній школі учні після вивчення числа і цифри 5 знайомляться з 0. Нуль з самого початку вводиться як характеристика порожньої множини. Поняття про 0 розкривається на основі використання прийому відлічування предметів по одному, шляхом віднімання рівних між собою чисел. Школярі повинні усвідомити: число 0 отримуємо тоді, якщо від будь-якого числа послідовно відняти всі його одиниці. Отже, нуль - це відсутність одиниць або предметів у множині і тому в числовому ряду його потрібно ставити ліворуч від 1. Пояснення того, що 0 означає відсутність одиниць якогось розряду у 1 класі давати не потрібно. При вивченні цього матеріалу використовують лінійку і показуючи на ній 0 пояснюють школярам, що з нього починається відлік: цифра 1 на лінійці означає кінець відрізка довжиною 1 см, а 0 позначає його початок. Серед чисел, які вивчаються в допоміжній школі, особливе місце посідає число 10, або 1 десяток. Лише при вивченні числа 10 можна показати відмінність між числом і цифрою (щоб записати число 10 потрібні дві цифри - 1 і 0). Цифра є умовним знаком, який використовується для позначення чисел, тобто символом. Вже це визначення вказує на трудність засвоєння цього поняття розумово відсталими учнями. Тому для того, щоб підвести школярів до розрізнення понять "число" і "цифра" потрібно, щоб вчитель на попередніх етапах навчання уважно слідкував за своїм мовленням і не допускав грубих помилок типу: "Яка цифра більша, 3 чи 2?": | ||||||
