Метод виклад з мат-ки 2. Спеціальна методика викладання математики зміст методика розв'язування арифметичних задач
 Скачать 7.16 Mb. Скачать 7.16 Mb.
|
|
Таку форму доцільно використовувати і при розв'язуванні іншого типу задач, наприклад: "Велосипедист за 4 години подолав відстань у 48 кілометрів, а автомобіль за 3 години - 180 км. Яка швидкість велосипедиста і автомобіля за годину?"
Наведемо ще один приклад. Задача: "Для того, щоб закласти сад, школа купила саджанці: 10 яблунь по 5 грн. за штуку, 15 вишень по 8 грн. за кожну і 20 кущів аґрусу по 2 грн. за кущ. Скільки грошей витратила школа за саджанці?" Короткий запис може мати такий вигляд:
Така форма запису хоча і абстрагує умову задачі, в той же час сприяє кращому усвідомленню її змісту та залежностей між даними і шуканими величинами. Також в допоміжній школі використовують схематичну форму запису задач. У більшості випадків вчителі використовують її у старших класах, коли в учнів вже сформовані навички робити короткий запис з використанням інших форм. Це тому, що її виконання передбачає достатній розвиток абстрактного мислення, адже відтворити умову за таким записом інколи буває досить складно. Наведемо приклади такого запису. 1. Мама в магазині купила на чотири гривні шоколаду, на 7 грн. - печива, а на гроші, що залишились, - цукерок. Всього мама потратила 20 грн. Скільки коштують цукерки? 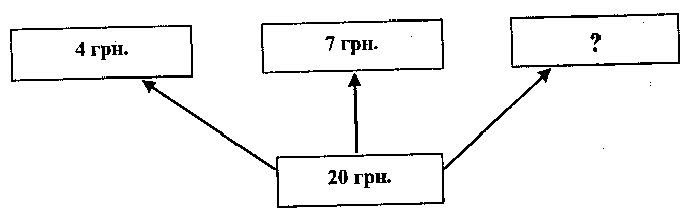 2. Для шкільної бібліотеки закупили книжки. Для дітей молодшого шкільного віку 360, для середнього - в 3 рази менше, а для старшого - в 2 рази більше, аніж для молодшого. Скільки всього книжок закупили для бібліотеки? 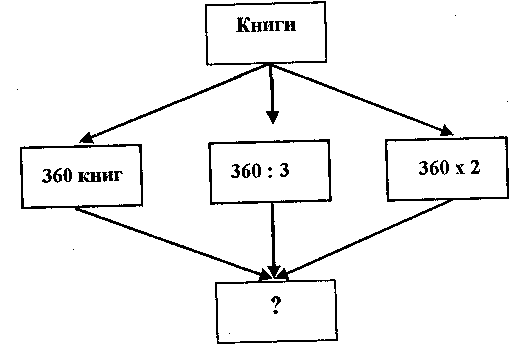 При розв'язуванні задач на збільшення чи зменшення чисел у кілька разів або на кілька одиниць, на кратне порівняння чисел тощо учням можна запропонувати схематичну форму запису умови При цьому потрібно дотримуватись пропорцій, які б відповідали числовим даним. Задача: "У одному ящику було 10 кг яблук, а в другому - у 2 рази більше. Скільки кілограмів яблук було у двох ящиках?" Короткий запис умови буде мати такий вигляд: 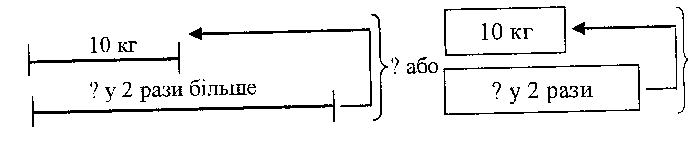 Якщо перед учнями під час розв'язування задачі немає підручника чи таблиці з умовою, тоді допускається використання дослівного запису її тексту. Це може бути застосовано і під час виконання контрольної роботи, при роботі над умовою нового типу арифметичної задачі, а також у тих випадках, коли ведуться спеціальні вправи по перетворенню дослівного запису в інший за своєю формою. У всіх інших випадках ця форма запису умови задачі себе не виправдовує. Самостійно зробити короткий запис умови задачі у будь-якій її формі розумово відсталі учні не можуть. їх цьому потрібно вчити. При цьому необхідно дотримуватись певної послідовності: 1) у 1-му класі, а також при ознайомленні учнів з новою формою запису умови задачі на наступних роках навчання, після того, як вчитель прочитав її зміст, він сам показує короткий запис на дошці. Учні слідкують за поясненням педагога і виконують його за ним у себе в зошитах; 2) на наступному етапі вчитель проводить розбір умови задачі разом з класом, а короткий запис виконує під його керівництвом один з викликаних до дошки учнів. При цьому йому пропонується прочитати одну закінчену смислову одиницю задачі і записати її коротко, потім другу і так далі; 3) наступна робота ускладнюється. Викликаному до дошки учневі пропонується прочитати задачу самостійно і виконати короткий запис під контролем вчителя. Учні класу теж виконують запис умови задачі самостійно і звіряють його з записом на дошці; 4) закінчується ця робота самостійним записом умови задачі учнями без будь-якої допомоги вчителя. 4) повторення задачі за запитаннями.. Після короткого запису умова задачі повторюється двома-трьома учнями. Повторення спочатку проводиться за запитаннями вчителя, потім школярі повторюють її в цілому самостійно. Здійснюючи запис умови задачі, повторюючи її за запитаннями, розумово відсталі учні проводять значну аналітико-синтетичну роботу: розчленовують її на складові частини, виділяють питання, числові дані, об'єднують їх за ознаками однорідності тих величин, до яких вони відносяться. Все це створює умови для знаходження оптимального шляху розв'язування задачі.   г) пошук розв'язування задачі. г) пошук розв'язування задачі. Після усвідомлення учнями тексту задачі вчитель переходить до її розбору, хоч в цілому ця робота розпочинається ще раніше – до її розбору, хоч в цілому ця робота розпочинається ще раніше при ознайомленні з умовою. Тепер вона повинна бути закінченою логічними міркуваннями у доступній розумово відсталим дітям формі. Розв'язування задачі - це виконання арифметичних дій відповідно до складеного плану.Кожна дія супроводжується розв'язанням, яке включає: а) формулювання питання, б) мотивацію вибору дії. Розбір задачі посідає центральне місце у її розв’язані. Для його проведення школярі повинні задіяти такі мисленнєві процеси, як аналіз і синтез. При цьому потрібно зазначити, що процес мислення, який йде від числових даних до питання задачі, називається синтетичним, а від питання задачі до числових даних – аналітичним. Продемонструємо кожен з цих процесів або способів розбору арифметичних задач на прикладі. Задача: Господарка купила на базарі 10 кг помідорів по 2 грн. за кілограм і 4 кг огірків по 3 грн. за кілограм. Скільки вона отримала здачі з 50 грн.?” При синтетичному способі розбору арифметичної задачі міркування можуть відбуватись таким чином: Вчитель (В.): Що купила господарка на базарі. Учень (У): Господарка на базарі купила помідори і огірки. В.: Скільки коштує 1 кг помідорів? У: 1 кг помідорів коштує 2 грн. В.: Скільки вона купила помідорів? У: Вона купила 10 кг. В.: На основі цих даних, що можна знайти? (Цим питанням ми пропонуємо учням виділити першу частину задачі). У: Ми можемо знайти скільки гривень коштують помідори. В.: Як це зробити? У, Потрібно по 2 грн. взяти 10 разів, буде 20 грн. В.: Що ще купувала господарка? У: Вона ще купувала огірки. В.: Скільки кілограмів огірків вона купила? У: Вона купила 4 кг огірків. В.: Скільки коштує 1 кг огірків? У: 1 кг огірків коштує 3 грн. В.: На основі цих даних, що ми можемо знайти? У: Ми можемо знайти, скільки гривень коштують огірки. В.: Як це зробити? У: Потрібно по 3 грн. взяти 4 рази, буде 12 грн. В.: Тепер ми знаємо, скільки господарка заплатила за помідори і скільки за огірки. На основі цих двох даних, що можна знайти? У.: Ми можемо взнати, скільки господарка заплатила за всю покупку. В.: Як це зробити? У: Для цього потрібно до суми, затраченої на купівлю помідорів, додати суму, витрачену на купівлю огірків: 20 грн. + 12 грн. = 32 грн. В.: Так скільки ж заплатила господарка за всі овочі? У.: За всі овочі вона заплатила 32 грн. В.: А скільки грошей у неї було? У: У неї було 50 грн. В.: Тепер ми можемо відповісти на головне запитання задачі? У: Так, можемо. В.: Як це зробити? У.: Для цього від усієї суми потрібно відняти суму, яку вона витратила на купівлю помідорів і огірків: 50 грн. – 32 грн. = 18 грн. В.: Так скільки гривень здачі отримала господарка? У: Господарка отримала 18 грн. здачі. Вчитель пропонує учням ще раз пригадати, як вони розв'язували задачу, яка дія була першою, яка друга, яка третя, яка відповідь задачі. Схематично синтаксичний спосіб розбору задачі буде мати такий вигляд (див. рис. 1.1.) Візьмемо цю саму задачу і розберемо її аналітичним способом. Міркування при аналітичному способі розбору умови арифметичної задачі буде проходити у такій формі: В.: Чи можна зразу взнати, скільки здачі отримала господарка? У.: Ні, не можна. В.: Чому не можна взнати зразу відповідь? (це питання примушує учнів виділити першу просту задачу.) У.: Ми не знаємо, скільки коштують помідори і огірки разом. В.: А ми знаємо, скільки кілограмів огірків купила господарка У.: Так, 4 кг. В.: А скільки коштує 1 кг огірків? У: 3 грн. В.: На основі цих даних, що можна знайти? У.: Ми можемо знайти, скільки коштують огірки. В.: Як це зробити? Рисунок 1.1. Схема синтетичного плану розбору задачі 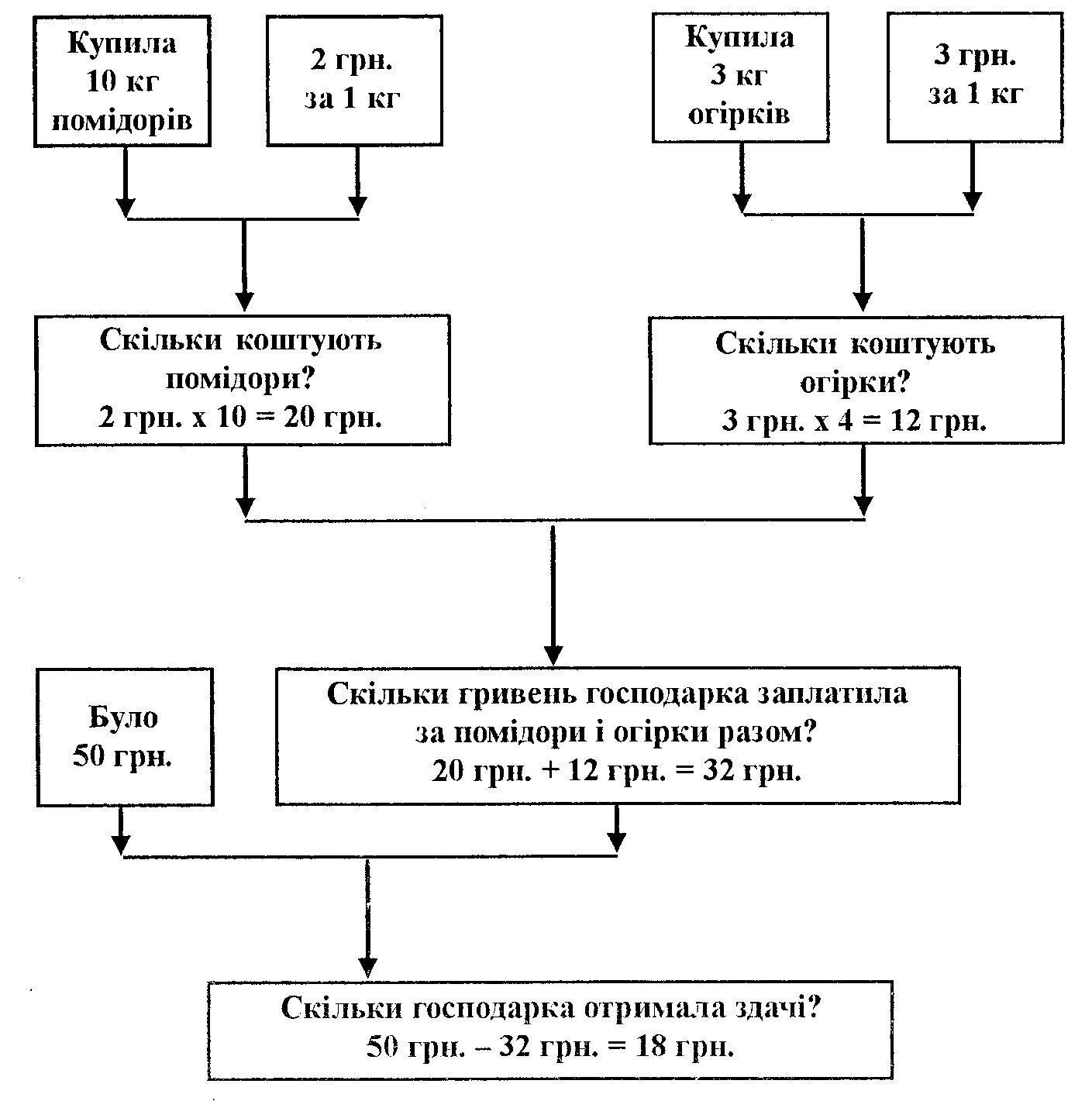 У: Потрібно по 3 грн. взяти 4 рази: 3 грн. х 4 = 12 грн. В.: Що ще купувала господарка? У.: Господарка купувала помідори. В.: Скільки кілограмів помідорів вона купила? У: Вона купила 10 кг помідорів. В.: Скільки коштує 1 кг помідорів? У: 1 кг помідорів коштує 2 грн. В.: На основі цих даних, що можна знайти? У.: Ми можемо знайти, скільки коштують помідори. В.: Як це зробити? У: Потрібно по 2 грн. взяти 10 разів, отримає 20 грн.: 2 грн. х 10 = 20 грн. В.: Тепер ми знаємо, скільки господарка заплатила за помідори і скільки за огірки. На основі цих даних, що ми можемо знайти? У.: Ми можемо знайти, скільки вона заплатила за всю покупку. В.: Як це зробити? У: Потрібно до суми, затраченої на покупку огірків, додати суму, витрачену на покупку помідорів: 12 грн. + 20 грн. = 32 грн. В.: Так скільки заплатила господарка за всі овочі? У.: За всі овочі господарка заплатила 32 грн. В.: А тепер можна відповісти на запитання задачі? У: Так, можемо. В.: Як це зробити? У: Потрібно від 50 грн. відняти суму, яку заплатила господарка за всю покупку: 50 грн. - 32 грн. = 18 грн. В.: Скільки гривень отримала здачі господарка? У: Господарка отримала 18 грн. здачі. В.: Давайте ще раз пригадаємо, як ми розв'язували задачу. Що ми взнали спочатку? Що потім? Яка відповідь задачі? Схематично аналітичний спосіб арифметичної задачі виглядає так (див. рис. 1.2.): Рисунок 1.2. Схема аналітичного способу розбору задачі 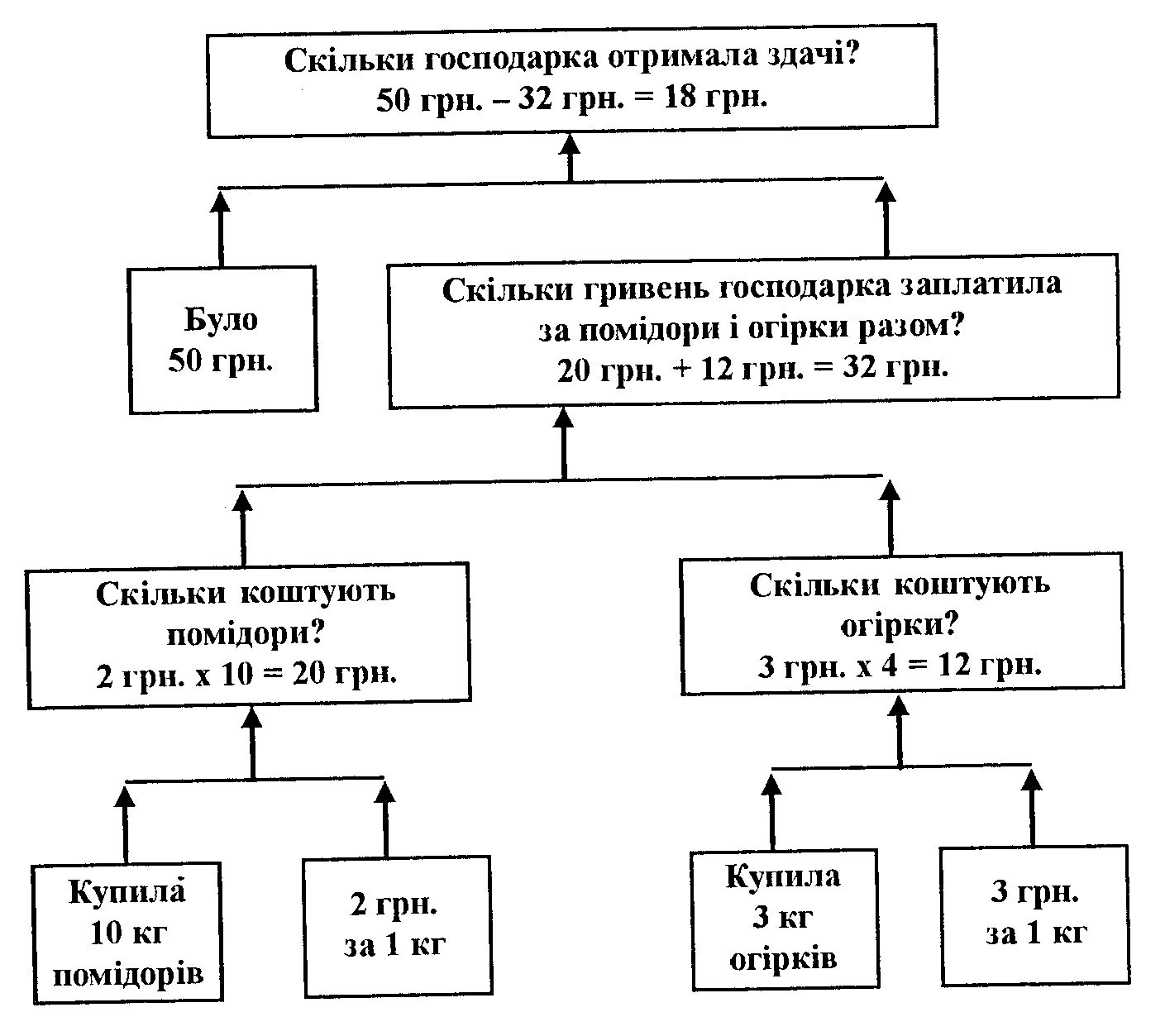 Наведені зразки розбору умови арифметичної задачі розкривають суть кожного способу у числовому вигляді. Найбільш поширеним у допоміжній школі є синтетичний спосіб, який веде думку школяра від відомого до невідомого. Аналітичний спосіб більш спрямований на складання плану розв'язування задачі. У допоміжній школі його потрібно застосовувати лише з 3-го класу. У дійсності розбір задачі є процес аналітико-синтетичний, а тому аналіз і синтез знаходиться у постійній взаємодії, доповнюючи один одного. Якщо думка учня починається з числових даних, то на передній план виступає синтез, а аналіз буде для нього супутником перевірки доцільності підбору чисел і дій над ними. Якщо за початок розбору береться питання задачі, тоді аналіз виступає на перший план, а синтез йому буде супутником. Аналітико-синтетичний спосіб розбору задачі значно впливає на розвиток логічного мислення розумово відсталих учнів, на їхнє мовлення. Обидва способи розбору замови арифметичної задачі мають як позитивні, так і негативні сторони. Зупинимося коротко на них.
Уже у процесі розбору задачі намічається план і послідовність Дій. Після її розбору учитель разом з дітьми з’ясовує, на скільки дій задача, яке перше питання і якою дією можна відповісти на нього,    яке друге питання і так далі. Усно складається послідовність дій. Після цього учні приступають до запису задачі. яке друге питання і так далі. Усно складається послідовність дій. Після цього учні приступають до запису задачі.ґ) розв'язування, запис задачі та формулювання відповіді. Під час виконання запису розв'язку задачі можуть використовуватись різні його варіанти: Перший. У 1-му класі, коли діти не знають усіх літер алфавіту, не можуть писати і читати, запис розв'язку дається у вигляді прикладу, розміщеного по середині рядка. Першокласникам можна запропонувати проілюструвати задачу малюнком, використовуючи для цього знайомі учням геометричні фігури - трикутники, круги, квадрати. Після виконання дії їх вчать давати коротке пояснення ходу розв'язування усно. По мірі вивчення літер алфавіту вводиться називання літерою з крапкою в дужках після числа тих предметів, над якими виконувалось обчислення: 5-3 = 2 (сл.) (сливи). Такий запис утруднює процес навчання розв'язуванню задач, оскільки питання вони сприймають на слух, отже, до роботи залучений слуховий аналізатор. В той час при записі учнями питання поряд зі слуховим в аналізі умови беруть участь ще й зоровий аналізатор та моторика. Але цей процес у 1 -му класі неминучий. Другий. Коли учні оволоділи навичками читання не тільки друкованого, а й рукописного тексту (2 клас) вчитель іноді може записувати питання плану на дошці для того, щоб учні змогли сприймати його не тільки на слух, ай через зір. Робити переписування питання в зошити школярам не потрібно. Це значно полегшить їм розуміння розв'язування задачі, підготує їх до майбутнього запису плану в зошиті. Вчитель шляхом усного опитування виявляє, чи правильно вони ставлять питання. Таким чином, у 2-му класі учні записують дію і пояснюють, що нею знайшли. Наприклад: "На огорожі сиділо 3 пташки, до них прилетіло ще 2 пташки. Скільки пташок сиділо на огорожі?” Запис розв'язання цієї задачі буде таким: 3 пт. + 2 пт. = 5 пт. Треба пам'ятати, що слова, які починаються на голосний, скорочуються, як правило, до наступного приголосного, який стоїть перед голосним (яблуко – ябл., ялинка - ял.). У короткому записі задач назви предметів дій (купили, продали, відрізали і т.п.) краще записувати повним словом. Щоб діти краще зрозуміли поняття "відповідь задачі", число, яке є відповіддю, можна підкреслити кольоровим олівцем, а на дошці - кольоровою крейдою. Третій. Починаючи з 3-го класу, в допоміжній школі використовуються декілька форм запису розв'язку задачі: а) Записуються окремі дії і відповідь задачі. Наприклад: "Купили 6 м зеленого шовку і 5 м блакитного. Ціна 1 м шовку обох кольорів однакова і дорівнює 20 грн. Скільки гривень коштує вся покупка?" Форма запису може мати такий вигляд:
Відповідь: 220 грн. б) Запис окремих дій з коротким коментарем до кожної з них. Вона отримала ще назву оповідної форми. Наприклад:
Відповідь: вся покупка коштує 220 гривень. в) Запис розв'язку задачі з письмовим планом (питальна форма). - записується перше питання і одразу дія до нього, друге питання і дія до нього і т.д.: План розв'язування: 1). Скільки коштують 6 метрів зеленого шовку? 20 грн. х 6 = 120 грн. 2). Скільки коштують 5 метрів блакитного шовку? 20грн. х5 = 100 грн. 3). Скільки гривень коштує вся покупка? 120 грн. + 100 грн. = 220 грн. Відповідь: вся покупка коштує 220 гривень. - записуються всі питання плану розв'язування, а потім розв'язок задачі: План 1). Скільки коштують 6 метрів зеленого шовку? 2). Скільки гривень коштують 5 метрів блакитного шовку?       3). Скільки гривень коштує вся покупка? 3). Скільки гривень коштує вся покупка? Розв'язок 1). 20 грн. х 6 = 120 грн. 2). 20 грн. х 5 = 100 грн. 3). 120 грн. + 100 грн. = 220 грн. Відповідь: вся покупка коштує 220 грн. - записуються спочатку всі дії, а потім до них складається план розв'язку задачі: Розв'язування 1). 20грн.х 6= 120 грн. 2). 20 грн. х 5 = 100 грн. 3). 120 грн. + 100 грн. = 220 грн. План 1). Скільки гривень коштують 6 метрів зеленого шовку? 2). Скільки гривень коштують 5 метрів блакитного шовку? 3). Скільки гривень коштує вся покупка? Відповідь: вся покупка коштує 220 грн. Вчити формулювати відповідь спочатку потрібно опираючись на питання задачі, лише замість слова скільки вставляти число, отримане у відповіді. (Питання задачі: Скільки гривень коштує вся покупка? Відповідь: 220 грн. коштує вся покупка). Також потрібно вказати, що відповідь може бути короткою - 220 грн.; або розгорнутою: вся покупка коштує 220 гривень. д) перевірка розв'язаної задачі. Ще під час обчислення прикладів учні робили перевірку їх правильності через знаходження одного з компонентів дії. Така ж робота обов'язково проводиться і при розв'язуванні задач. Перевірка допомагає уясувати, з одного боку, чи правильно вона виконана, чи допущені помилки, визначити, чи зрозуміли учні задачу, чи відповідає відповідь її умові. З іншого - це засіб визначення прогалин у знаннях школярів. Позитивна риса перевірки полягає ще й в тому, що вона дає дітям можливість контролювати свою роботу і тим самим створює умови для більшої їх самостійності при розв'язуванні задачі. Які ж прийоми перевірки використовуються в допоміжній школі? 1) Перевірка шляхом практичних дій. Якщо числові дані умови задачі невеликі, перевірку можна здійснити шляхом практичних дій з множинами. Наприклад: "У хлопчика було 10 морквин, 4 моркви він віддав кролям. Скільки морквин залишилося у хлопчика?" 10 (морк.) – 4 (морк.) = 6 (морк.) Відповідь: 6 морквин. Перевірка. Після розв'язання задачі учень бере морквини, які залишилися (6 штук) і додає до них 4 морквини. В сумі він отримує стільки, скільки їх було дано в умові задачі - 10 штук. Отже, задача розв'язана правильно. 2) Встановлення відповідності між числами, знайденими внаслідок розв'язування задачі і заданими числами. Це найбільш поширений прийом перевірки задачі в допоміжній школі. Суть його полягає в тому, що виконуючи арифметичні дії, учні повинні отримати ті числа, які є в умові. В такому випадку така задача вважається розв'язаною вірно. Наприклад: "В автобусі їхало 40 пасажирів. На першій зупинці зійшло 10 пасажирів, а на другій - 5 пасажирів. Скільки пасажирів залишилося в автобусі?” 1) 10 (пас.) + 5 (пас.) = 15 (пас.) 2) 40 (пас.) - 15 (пас.) = 25 (пас.) Відповідь: 25 пасажирів. Перевірка. Відомо, що в автобусі залишилося 25 пасажирів. Першою дією ми взнаємо, скільки пасажирів вийшло з автобуса. їх було 15. Якщо до 25 додати 15, буде 40 пасажирів. Отже, задача розв'язана правильно. 3) Порівняння результату, який дістали учні в процесі розв'язування задачі, з відповіддю вчителя. Цей прийом є одним з елементів програмованого навчання. При його використанні вчитель пише на дошці проміжні результати і кінцеву відповідь не в тому порядку, в якому вимагає задача. Відповіді закриваються і показуються лише після того, як задача розв'язана учнями. Вони звіряють свої відповіді з відповідями, даними на дошці. При помилковому розв'язанні дії чи задачі в цілому школяр шукає нові шляхи її розв'язання.        4) В старших класах при роботі над задачами на дві дії учням можна запропонувати більш складний прийом перевірки правильності її розв'язання. Це складання до даної задачі оберненої задачі. 4) В старших класах при роботі над задачами на дві дії учням можна запропонувати більш складний прийом перевірки правильності її розв'язання. Це складання до даної задачі оберненої задачі.Кількість обернених задач залежить від кількості числових даних в умові задачі. Вони досить позитивно впливають на розвиток логічного мислення розумово відсталих учнів. Наприклад: "У зоопарку 6 бурих і 2 білих ведмеді. Всіх їх розмістили у 4 вольєри порівно. Скільки ведмедів було у кожному вольєрі?". (Відповідь: по два ведмедя). Міркування доцільно провести використовуючи декілька варіантів: "Давайте перевіримо розв'язання задачі. Для цього ми складемо і розв'яжемо обернену задачу. а) Відомо, що у кожному вольєрі знаходилось по 2 ведмеді, а от скільки вольєрів для цього потрібно - ми не знаємо. Давайте сформулюємо задачу: "У зоопарку було 6 бурих ведмедів і 2 білих ведмеді. Усіх їх розмістили порівну - по 2 ведмеді у кожному. Скільки потрібно вольєрів для розміщення всіх ведмедів?" Розв'язання:
Відповідь: для розміщення ведмедів необхідно 4 вольєри. б) Відомо, що у кожному вольєрі помістили по 2 ведмеді. Вольєрів було 4, а бурих ведмедів 6. Сформулюємо задачу: "У зоопарку було 6 бурих і декілька білих ведмедів. Всіх їх розмістили у 4 вольєри порівну: по 2 ведмеді у кожному. Скільки було білих ведмедів у зоопарку? " Розв'язання:
Відповідь: в зоопарку було 2 білих ведмедя. в) Відомо, що у кожен вольєр помістили по 2 ведмеді. Вольєрів було всього 4, а білих ведмедів 2. Сформулюємо задачу: "У зоопарку було декілька бурих ведмедів і 2 білих ведмеді. Всіх їх розмістили у 4 вольєри порівну: по 2 ведмеді у кожен вольєр. Скільки бурих ведмедів було у зоопарку?" Розв'язання:
Відповідь: в зоопарку було 6 бурих ведмедів. 5) Одним з найпростіших прийомів перевірки правильності розв'язання задачі у старших класах є звіряння здобутої відповіді з тією, що в підручнику. Якщо відповіді однакові, то учень робить висновок, що завдання виконано правильно, а якщо різні, то шукає помилки. Учитель ретельно відбирає задачі при первинному ознайомленні учнів з перевіркою їх розв'язання. Для цього краще всього підбирати задачі в одну дію і поступово переходити до перевірки задач з двома, а потім і більше діями. е) закріплення розв'язаної задачі. Учні допоміжної школи навіть одного і того ж класу мають різні можливості у засвоєнні навчального матеріалу, і вчитель не може бути впевненим у тому, що всі вони зрозуміли розв'язання задачі. Це вимагає від нього проведення роботи на закріплення. Вона проводиться з застосуванням різних прийомів. Для прикладу візьмемо задачу про ведмедів, яку ми описали вище. 1) Вчитель ставить опорні питання до змісту задачі. Наприклад:
Для закріплення способу розв'язування задач певного типу необхідно розв'язання достатньої їх кількості. Задачі певного типу слід пропонувати не підряд, а розрізнено, щоб позбавитись "натаскування" учнів в процесі їхнього розв'язування.     є) подальша робота над розв'язаною задачею. Кращому розумінню предметної ситуації і залежностей між даними допоможе учням подальша робота над розв'язаною задачею. З цією метою застосовуються наступні прийоми.
3) Заміна питання так, щоб задача на дві дії розв'язувалась як на одну. Наприклад: - Скільки олівців у другій коробці?
|
