ИДЗ №1. Среди 20 лотерейных билетов 4 выигрышных. Наудачу взяли 6 билетов. Определить вероятность того, что среди них хотя бы 2 выигрышных

• Название: Среди 20 лотерейных билетов 4 выигрышных. Наудачу взяли 6 билетов. Определить вероятность того, что среди них хотя бы 2 выигрышных
• Дата: 22.03.2022
• Размер: 370.5 Kb.
• Имя файла: ИДЗ №1.doc
• Тип: Документы; #409513
• страница: 3 из 11

Вариант 5

1. 
   Из колоды содержащей 36 карты вынимается наугад 5. Найти вероятность того, что это две шестерки, две семёрки и туз.
   
2. 
   Найти вероятность того, что корни уравнения вещественны, если коэффициенты и любые числа, удовлетворяющие условиям: .
   
3. 
   Система S состоит из двух независимых дублирующих блоков аbс_k (k = 1,2). Блок аbс_kсостоит из трех последовательно соединенных блоков а_k , b_k и с_k
   

Найти надежность системы – вероятность того, что система будет исправна в течении некоторого времени, если известны надежности блоков P(а_k) = 0.9, P(b_k) = 0.9, P(с_k) = 0.8.

4. 
   Три спортсмена стреляют по мишени. Вероятность попадания в мишень для первого спортсмена 0,9, для второго 0,6, для третьего 0,5. Какова вероятность того, что: а) мишень будет поражена только одним спортсменом; б) мишень будет поражена хотя бы одним спортсменом; в) мишень не будет поражена?
   
5. 
   Для проверки геодезических работ назначена группа экспертов, состоящая из трех подгрупп. В первой подгруппе - 2 человека, во второй - 4 и в третьей - 5. Эксперты первой подгруппы принимают верное решение с вероятностью 0,9, эксперты второй подгруппы c вероятностью 0,8, эксперты третьей подгруппы с вероятностью 0,7. Наудачу вызванный эксперт принимает 3 независимых решения. Найти вероятность того, что принимал решения эксперт из первой подгруппы, если все 3 решения приняты верно.
   
6. 
   Вероятность выигрыша в лотерею на один билет равна 0,15. Куплено 14 билетов. Найти наивероятнейшее число выигравших билетов и соответствующую вероятность.
   
7. 
   
   Пара игральных костей подбрасывается 10 раз. Какова вероятность, что сумма очков, равная 10, выпадет более 2 раз?
   
8. 
   Из 100 изделий, среди которых имеется 30 изделий 1-го сорта и 70 изделий 2-го сорта, выбраны случайным образом 30 изделий. Определить вероятность того, что среди выбранных изделий окажется не менее 10 и не более 20 изделий 1 сорта. Указать, как точно определяется данная вероятность, и вычислить, используя одну из приближенных формул.
   
9. 
   Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,003. Поступило 600 вызовов. Определить вероятность того, что будет более 2 «сбоев».
   
10. 
    Всхожесть семян составляет 60%. Пусть - число взошедших семян из 1000 посеянных. Используя приближенную формулу Муавра-Лапласа, определить число , для которого .
    

Вариант 6

1. 
   Из полной колоды карт (36 листов) вынимается 4 карты. Найти вероятность того, что все карты разной масти.
   
2. 
   Два судна могут подойти к причалу в любое время в течение суток независимо. На причале одно место для разгрузки. Разгрузка длится 2 часа. Какова вероятность того, что одному из судов придется ждать.
   
3. 
   Система S состоит из трех независимых подсистем S_а , S_b и S_c. Неисправность хотя бы одной подсистемы ведет к неисправности всей системы (подсистемы соединены последовательно). Подсистемы S_а и S_b состоят из двух независимых дублирующих блоков а_k и b_k (k = 1,2) (схема параллельного подсоединения блоков в подсистемах).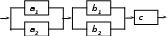
   

Найти надежность системы – вероятность того, что система будет исправна в течении некоторого времени, если известны надежности блоков P(а_k) = 0.8, P(b_k) = 0.9, P(с) = 0.85.

4. 
   В двух партиях процент доброкачественных изделий 70 и 45 соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них: а) хотя бы одно бракованное; б) два бракованных; в) одно доброкачественное и одно бракованное?
   
5. 
   Испытывается прибор, состоящий из двух узлов а и b, соединенных последовательно в смысле надежности. Надежности (вероятности безотказной работы за время Т) узлов а и b известны и равны P(а) = 0.8, P(b) = 0.7 . Узлы отказывают независимо друг от друга. По истечении времени Т выяснилось, что прибор неисправен. Найти с учетом этого вероятность того, что неисправны оба узла.
   
6. 
   Для проверки геодезических работ назначена группа экспертов, состоящая из трех подгрупп. В первой подгруппе - 4 человека, во второй - 3 и в третьей - 2. Эксперты первой подгруппы принимают верное решение с вероятностью 0,6, эксперты второй подгруппы c вероятностью 0,7, эксперты третьей подгруппы с вероятностью 0,8. Наудачу вызванный эксперт принимает 5 независимых решений. Найти вероятность того, что: а) ровно 3 решения приняты верно; б) принимал решения эксперт из первой подгруппы, если 3 решения приняты верно.
   
7. 
   На каждый лотерейный билет с вероятностью 0,06 может выпасть крупный выигрыш, с вероятностью 0,2 - мелкий выигрыш и с вероятностью 0,74 билет может оказаться без выигрыша. Куплено 14 билетов. Определить вероятность получения 2 крупных выигрышей и 3 мелких.
   
8. 
   Из 200 изделий, среди которых имеется 50 изделий 1-го сорта и 150 изделий 2-го сорта, выбраны случайным образом 50 изделий. Определить вероятность того, что среди выбранных изделий окажется не менее 20 изделий 1 сорта. Указать, как точно определяется данная вероятность, и вычислить, используя одну из приближенных формул.
   
9. 
   Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,002. Поступило 600 вызовов. Определить вероятность того, что будет не более 1 «сбоя».
   
10. 
    Всхожесть семян составляет 70%. Пусть - число взошедших семян из 500 посеянных. Используя приближенную формулу Муавра-Лапласа, определить число , для которого .