ИДЗ №1. Среди 20 лотерейных билетов 4 выигрышных. Наудачу взяли 6 билетов. Определить вероятность того, что среди них хотя бы 2 выигрышных

• Название: Среди 20 лотерейных билетов 4 выигрышных. Наудачу взяли 6 билетов. Определить вероятность того, что среди них хотя бы 2 выигрышных
• Дата: 22.03.2022
• Размер: 370.5 Kb.
• Имя файла: ИДЗ №1.doc
• Тип: Документы; #409513
• страница: 8 из 11

Вариант 15

1. 
   Из колоды в 52 карты (по 13 карт каждой масти) отбирается 5 карт. Какова вероятность получить комбинацию "каре" - четыре карты одного номинала?
   
2. 
   На отрезках [0,1] и [1,3] наудачу и независимо друг от друга выбираются две точки A, B. Найти вероятность того, что расстояние между ними не превосходит 1.
   
3. 
   Система S состоит из подсистемы S_аbс, состоящей из двух независимых дублирующих блоков аbс_k (k = 1,2) (схема параллельного подсоединения блоков в подсистемах). Блок аbс_kсостоит из трех последовательно соединенных блоков а_k , b_k и с_k
   

Найти надежность системы – вероятность того, что система будет исправна в течении некоторого времени, если известны надежности блоков P(а_k) = 0.9, P(b_k) = 0.9, P(с_k) = 0.8.

4. 
   В двух партиях процент доброкачественных изделий 70 и 40 соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них: а) хотя бы одно бракованное; б) два бракованных; в) одно доброкачественное и одно бракованное?
   
5. 
   В альбоме 8 чистых и 5 гашеных марок. Из них наудачу извлекаются 4 марки, подвергаются спецгашению и возвращаются в альбом. После этого вновь наудачу извлекается 4 марки. Определить вероятность того, что все они чистые.
   
6. 
   В магазин поступают однотипные изделия с трех заводов, причем первый завод поставляет 50 % изделий, второй - 30%, а третий – 20% изделий. Среди изделий 1-го завода 70% первосортных, второго – 80%, третьего – 90%. Куплено одно изделие. Оно оказалось первосортным. Определить вероятность того, что купленное изделие выпущено первым заводом.
   
7. 
   На каждый лотерейный билет с вероятностью 0,1 может выпасть крупный выигрыш, с вероятностью 0,2 - мелкий выигрыш и с вероятностью 0,7 билет может оказаться без выигрыша. Куплено 15 билетов. Определить вероятность получения 1 крупного выигрыша и 2 мелких.
   
8. 
   Из 100 изделий, среди которых имеется 40 изделий 1 сорта и 60 изделий 2 сорта, выбраны случайным образом 12 изделий для проверки их качества. Определить вероятность того, что среди выбранных изделий окажется не менее 4 и не более 6 изделий первого сорта (указать, как точно определяется данная вероятность, и вычислить, используя одну из приближенных формул).
   
9. 
   Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,03. Поступило 100 вызовов. Определить вероятность ровно 3 «сбоев».
   
10. 
    Используя приближенную формулу Муавра-Лапласа, определить сколько раз минимум необходимо подбросить монету, чтобы с вероятностью 0,99 ожидать, что относительная частота выпадения орла в этой серии подбрасываний будет отличаться от вероятности выпадения орла при одном подбрасывании не более, чем на 0,005.
    

Вариант 16

1. 
   
   Колода карт (36 листов) делится на две равные части. Какова вероятность, что в каждую пачку попадет по два туза?
   
2. 
   Найти вероятность того, что корни уравнения вещественны, если коэффициенты и любые числа, по абсолютной величине не превышающие 1/2.
   
3. 
   Система S состоит из трех независимых подсистем S_а , S_b и S_c. Неисправность хотя бы одной подсистемы ведет к неисправности всей системы (подсистемы соединены последовательно). Подсистемы S_а и S_b состоят из двух независимых дублирующих блоков а_k и b_k (k = 1,2) (схема параллельного подсоединения блоков в подсистемах).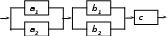
   

Найти надежность системы – вероятность того, что система будет исправна в течении некоторого времени, если известны надежности блоков P(а_k) = 0.8, P(b_k) = 0.9, P(с) = 0.85

4. 
   В двух партиях процент доброкачественных изделий 75 и 35 соответственно. Наудачу выбирают по одному изделию из каждой партии. Какова вероятность обнаружить среди них: а) хотя бы одно бракованное; б) два бракованных; в) одно доброкачественное и одно бракованное?
   
5. 
   Прибор состоит из двух дублирующих друг друга узлов а и b и стабилизатора напряжения , работающего в двух режимах. При работе стабилизатора в первом режиме с вероятностью 0.8 надежность узлов P(а) = 0.9, P(b) = 0.95. При работе стабилизатора во втором режиме надежность узлов P(а) = 0.5, P(b) = 0.6. Найти надежность прибора, если узлы независимы.
   
6. 
   В магазин поступают однотипные изделия с трех заводов, причем первый завод поставляет 60 % изделий, второй - 30%, а третий – 10% изделий. Среди изделий 1-го завода 50% первосортных, второго – 80%, третьего – 95%. Куплено одно изделие. Оно оказалось первосортным. Определить вероятность того, что купленное изделие выпущено первым заводом.
   
7. 
   На каждый лотерейный билет с вероятностью 0,15 может выпасть крупный выигрыш, с вероятностью 0,15 - мелкий выигрыш и с вероятностью 0,7 билет может оказаться без выигрыша. Куплено 15 билетов. Определить вероятность получения 2 крупных выигрышей и 1 мелкого.
   
8. 
   Из 90 изделий, среди которых имеется 30 нестандартных, выбраны случайным образом 5 изделий для проверки их качества. Определить вероятность того, что среди выбранных изделий окажется хотя бы 2 нестандартных изделия (указать, как точно определяется данная вероятность, и вычислить, используя одну из приближенных формул).
   
9. 
   Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,004. Поступило 500 вызовов. Определить вероятность менее 6 «сбоев».
   
10. 
    Каждый кекс содержит в среднем 6 изюминок (предполагается, что при выпечке каждая из изюминок с равной вероятностью может попасть в любой из кексов). Используя приближенную формулу Муавра-Лапласа, определить с вероятностью 0,9, сколько максимум в партии из 1000 кексов содержится кексов без изюминок (определить число , для которого , где - число кексов без изюминок).